OBRAZ CYFROWY?
Jest to uporządkowany zbiór pikseli w postaci np. macierzy z przypisanymi do nich jasnościami spektralnymi lub poziomami szarości zapisanymi na nośniki danych najczęściej na stronę bajtową tzn. stopień szarości pojedynczego piksela jest opisywany cyfrowo w granicach 0 (czerń) do 2 55 (biel) tg 28 = 256 poziomów szarości, położenie piksela w obrazie oznaczają rzędy i kolumny macierzy tj. wsp. płaskie obrazu.
34. Definicja obrazu cyfrowego
Jest to uporządkowany zbiór pikseli w postaci np. macierzy z przypisanymi do nich jasnościami spektralnymi lub poziomami szarości zapisanymi na nośniki danych najczęściej ma strukturę bajtową tzn. stopień szarości pojedynczego piksela jest opisywany cyfrowo w granicach 0 (czerń) do 255 (biel) tj: 28 = 256 poziomów szarości, położenie piksela w obrazie oznaczają rzędy i kolumny macierzy tj. wsp. płaskie obrazu.
Obrazy cyfrowe otrzymuje się na wyjściu takich urządzeń jak :
Skanery
Radiometry
Systemy mikrofalowe
Kamery CCD
Dane cyfrowe otrzymujemy również skanując istniejące zdjęcie
35. DYSKRETYZACJA I KWANTYZACJA (ZAPIS OBRAZU CYFROWEGO)
Dyskretyzacja - przedstawienie obrazu w określonej liczbie pikseli. Mówi o tym w ilu pikselach został zapisany dany obraz.
Kwantyzacja - przypisanie odpowiednim pikselom których położenie jest już zidentyfikowane w matrycy odpowiednich poziomów szarości. Obraz powinien być kwantyzowany przy jak największej liczbie k.
36. UKŁAD WSPÓŁRZĘDNYCH PISELOWYCH.
standardowo może być zdefiniowany tak, że początek układu współrzędnych jest w lewym górnym rogu matrycy
- jest prostokątny to trzeba uwzględnić jego wymiar przy przejściu od układu współrzędnych pikselowych na układ tłowy
Przejście z jednego układu do drugiego
x'=(x'-x'p)*psx
z kładu pikselowego do tłowego
y'=(y'p-y')*psy
psx-wymiar piksela wzdłuż osi odciętych
37. CECHY OBRAZU CYFROWEGO
Geometryczne - rozdzielczość powierzchniowa-wymiar piksela w terenie
określają geometrię obrazu
wymiar obrazu.
Liczbę pikseli na cal
Wymiar pxl
Układ wsp. pxl w lewym górnym narożniku
Radiomatyczne - rozdzielczość radiomatyczna-opisuję zasięg oraz dająca się wyróżnić liczbę określającą dyskretne wartości jasności
6 bit, 8 bitowy, 24 bit, 32 bi-czyli ilość bitów potrzebnych do zapisania obrazu cyfrowego
jasność obrazu cyfrowego
kontrastowość obrazu cyfrowego
Spektralne - rejestracja może dotyczyć określanego wspólnego zakresu fal elektromagnetycznych.
38. ANALIZA OBRAZU CYFROWEGO - HISTOGRAM OBRAZU
Histogram obrazu cyfrowego-jest to określenie z jaką częstotliwością występują piksele o określonym poziomie szarości. Przedstawiony w postaci wykresu, tabel (jest to statystyczny rozkład skali szarości w funkcji liczby pikseli)
Możemy go zmienić:
przez zastosowanie procesu wyrównania - histogram sprawdzamy przy wyrównaniu do stanu gdy częstotliwości występowania pikseli o podobnym stopniu szarości jest jednakowa. Zmienne są wartości poziomu szarości przypisane każdemu pikselowi
normalizacja histogramu - histogram jest sprawdzany do krzywej Gaussa - rozkład częstotliwości odpowiada krzywej Gaussa.
38. Analiza obrazu cyfrowego - histogram obrazu
Histogram obrazu cyfrowego-jest to określenie z jaką częstotliwością występują piksele o określonym poziomie szarości. Przedstawiony w postaci wykresu, tabel (jest to statystyczny rozkład skali szarości w funkcji liczby pikseli)
Możemy go zmienić:
przez zastosowanie procesu wyrównania - histogram sprawdzamy przy wyrównaniu do stanu gdy częstotliwości występowania pikseli o podobnym stopniu szarości jest jednakowa. Zmienne są wartości poziomu szarości przypisane każdemu pikselowi
normalizacja histogramu - histogram jest sprawdzany do krzywej Gaussa - rozkład częstotliwości odpowiada krzywej Gaussa.
39 METODY POPRAWIENIA JAKOŚCI OBRAZU CYFROWEGO
- sprowadzenie ...... do krzywej Gaussa
- wyrównanie histogramu zakładamy pewien poziom szarości do wyrównania
- rozciągnięcie histogramu - poprawienie kontrastu;
- filtracja obrazu - np. w celu wyeliminowania szumów.
Interpretacja przez histogram:
obraz ciemny
b) obraz jasny
c) obraz kontrastowy
d) obraz małokontrastowy
39. Metody poprawienia jakości obrazu cyfrowego
normalizacja histogramu - histogram jest sprawdzany do krzywej Gaussa - rozkład częstotliwości odpowiada krzywej Gaussa.
wyrównanie histogramu zakładamy pewien poziom szarości do wyrównania
rozciągnięcie histogramu - poprawienie kontrastu;
filtracja obrazu - np. w celu wyeliminowania szumów.
40. FILTRACJA OBRAZU CYFROWEGO - RODZAJE FILTRÓW I ICH ZASTOSOWANIE.
Filtrowanie - ma na celu polepszenie jakości zdjęcia.
Przyczyny pogorszenia jakości obrazu:
zakłócenie w transmisji danych cyfrowych pracy sensora;
zła ostrość;
dodatkowe szumy;
błąd sensora.
Metody filtracji:
przestrzenne i częstotliwościowe.
liniowe i nieliniowe.
Najpopularniejszy podział filtrów:
dolnoprzepustowe - do eliminacji szumu na skutek digitalizacji, defektu poziomu szarości na skutek błędu szarości kamery - wygładzają szczegóły w obrazie, zmniejszają poziom kontrastu obrazu cyfrowego ( rozmazanie i nieostrość krawędzi), wygaszanie wysokich częstotliwości.
górnoprzepustowe - wzmacniają krawędzie i wyodrębniają ostre zmiany intensywności w obrazie, tłumi niskie częstotliwości.
środkowoprzepustowe - najrzadziej stosowane ( do wyodrębniania określonych szczegółów).
Filtry
obraz cyfrowy reprezentowany jest przez 3 wymiar ( wsp. pikselowe x, y i poziom szarości)
filtrem jest macierz o określonych wartościach przez które mnożymy obraz wyjściowy ( pierwotny)
Wyznaczana jest nowa wartość
wsp. 
jest to filtr uśredniający
filtrowanie jest procesem stratnym, bo ostatnia kolumna i ostatni wiersz po filtrowaniu są czarnymi pasami ale dzięki funkcji ob. cyfr. jest to eliminowane ;
filtr uśredniający - tłumaczenie częstotliwościowych zakłóceń oraz tłumaczenie poziomów szarości dla krawędzi o wysokim poziomie szarości - ten filtr ma małe znaczenie, średnia wartość z przedziału zmniejsza błędy, zmniejsza ostrość krawędzi;
gdy zakłócenie obejmuje pojedynczy piksel to możemy zastosować filtr:

- gdy zakłócenie jest linią poziomą to stosujemy filtr:

- gdy zakłócenie jest linią pionową to stosujemy filtr:

Inne filtry
- filtrowanie za pomocą filtrów medianowych - określenie mediany, czyli przyporządkowanie nowego piksela wartości średniej z określonego przedziału;
usunięcie pojedynczych zakłóceń za pomocą lokalnej mediany;
41. METODY INTERPOLACJI OBRAZU CYFROWEGO.
algorytmy zmieniające poziom szarości danego piksela w odpowiedni dla jego otoczenia ( interpolacja powoduje wygładzenie obrazu - przechodzimy ze strony pikselowej do półtonowej)
metoda najbliższego sąsiada - zaokrąglana jest współrz. danego piksela do najbliższego pełnego piksela ( piksel przejmuje jasność od najbliższego sąsiada)
bilinearna - realizowane jest sąsiedztwo 4 najbliższych pikseli. Nowy piksel ma nowy poziom szarości wynikający z 4 sąsiadujących pikseli (nie jest to śr. arytmetyczna )
bikubiczna - piksel otrzymuje nowy poziom szarości wynikający z sąsiednich 16 pikseli (4x4)
42. PIRAMIDY OBRAZÓW.
Piramida jednokrotna - obraz pierwotny zdegradowany
( została zmniejsz. Dla jego rozdzielczości)
Piramida obrazów - stopniowo zmniejsza się rozdzielczość obrazu pierwotnego, by uzyskać szybkość wyświetlania i pozycjonowania obrazów, Schemat:
3 2
6 4
1 2 8
2 5 6
proces tworzenia piramidy obrazu - hierarchiczna wielopoziomowa korelacja;
machting - dopasowanie obrazów
Metody tworzenia obrazów piramidalnych -służą do przyspieszania procesu pomiarowego i szybszego wyznaczania położenia obiektów:
wysuwamy z obrazu pierwotnego co drugi wiersz i co drugą kolumnę obrazu cyfrowego;
uśredniamy wartości sąsiednich wierszy i kolumn obrazu cyfrowego;
zastosowanie jednej z czterech metod interpolacji;
metody związane z wygładzaniem.
43
44
45. FIZJOLOGICZNE PODSTAWY STEREOSKOPOWEGO WIDZENIA.
Każde oko zajmuje inne położenie w przestrzeni i obrazy powstałe w każdym oku są różne. Właściwość kojarzenia takich dwoch obrazów w jeden obraz przestrzenny nazywamy zdolnością widzenia stereoskopowego. Widzenie takie, które jest niejako wcięciem w przód, umozliwia ocenę przedmiotów we wszystkich trzech wymiarach, a także pozwala oceniać odległości.
najdłuższa odległść R, przy której można jeszcze odróżnić położenie punktów dotyczące uszeregowania w głąb nazywamy promieniem nieuzbrojonego widzenia stereoskopowego jest on dla rozstawu oczu b0 = 65 mm, ostrości stereoskopowegowidz. ustalonej doświadcz. γ = 30'' wynosi Rmax (b0/γ)*Q = 450 m
minimalny kąt widzenia w płaszczyźnie pionowej wynosi 1500 , a w poziomej 1200,
120 mln prążków w oku reaguje na światło, ale nie rozpoznaje barw
plamka żółta posiada największą czułość;
punkt ślepy - przyczepiony do nerwu wzrokowego;
paralaksa - różnica odległości Pi'P' oraz Pi''P'';
akomodacja - zdolność oka do widzenia ostro w różnych odległościach;
rozdzielczość dla obserwacji monokularnych -1min., dla obserwacji dwóch linii 5-10 sek
widzenie stereoskopowe δi = γ-γi to jest równoznaczne z powstaniem różnicy, czyli paralaksy pi = Pi'P' - Pi''P''
paralaksa fizjologiczna waha się od 17-50 s, min. 10-25 sek.
Zdolność rozdzielcza ( przy odległości dobrego widzenia 250 mm) wynosi 0,07 mm
46. METODY OTRZYMYWANIA EFEKTU STEREOSKOPOWEGO
1. Sposób optyczny
Polega on na rozdzieleniu promieni biegnących od lewego zdjęcia do lewego oka i promieni biegnących od prawego zdjęcia do prawego oka za pomocą specjalnych układów optycznych. Najprostszym układem optycznym służącym dla wymienionego celu jest stereoskop zwierciadlany.
2. Sposób anaglifowy
Polega na połączeniu dwóch obrazów, tego samego obiektu, zabarwionych dopełniającymi się kolorami i obserwacji ich przez filtry optyczne (barwne) tak dobrane, aby każde oko widziało tylko jeden obraz.
3. Sposób wirujących przesłon
Polega na przemiennym rzutowaniu obrazu lewego zdjęcia i prawego zdjęcia. Do przemiennego rzutowania używane są dyski z wyciętymi rowkami.
4. Sposób polaroidów
Podobny do sposobu anaglifowego, z tym, że dla rozdzielenia obrazów - zamiast kolorowych filtrów - stosowane są polaryzatory optyczne. Działanie tych polaryzatorów polega na uporządkowaniu drgań fal świetlnych w jednej wybranej płaszczyźnie.
5. Sposób rastrów
Polega na równoczesnym rzutowaniu dwu zdjęć poprzez siatki linii równoległych, co prowadzi nie tylko do uzyskania modelu stereoskopowego, ale także linii na tym modelu, które są odpowiednikami warstwic.
6. Sposób holograficzny
Różni się zdecydowanie od wszystkich metod możliwością bezsoczewkowego uzyskania modelu stereoskopowego za pomocą światła spójnego.
47. MODEL STEREOSKOPOWY - WARUNKI OPTYCZNE I GEOMETRYCZNE SZTUCZNEGO EFEKTU STEREOSKOPOWEGO WIDZENIA
Uzyskanie modelu stereoskopowego uzależnione jest od pewnych czynników:
Czynniki związane z procesem fotografowania:
Wykonanie zdjęć z dwóch różnych punktów przestrzeni (baz fotografowania) - podobna odległość od obiektu,
Wykonanie takich zdjęć żeby skale zdjęci lewego i prawego były w przybliżeniu jednakowe (dopuszczalna różnica 15%)
Promienie rzutujące wykonanych zdjęć nie powinny przecinać się pod kątem większym od 15º.
Pokrycie podłużne zdjęć 60%, poprzeczne 20 - 40%.
Czynniki ograniczające uzyskanie efektu stereoskopowego:
Konieczność prowadzenia obserwacji punktów modelu stereoskopowego w płaszczyznach rdzennych
Prowadzenie obserwacji zdjęć z odległości najlepszego widzenia
Odpowiednie ułożenie zdjęć do obserwacji (zdjęcie lewe stereogramu powinno być obserwowane lewym okiem, a prawe zdjęcie - prawym
max format zdjęć 18*18 cm
pomiar x', y', Px, Py
dokładność pomiaru współrzędnych tłowych ok. 10M m
znaczek pomiarowy wyobrażalny
max format 24*24 cm
dokł. ok. 3M m
pomiar x', y', Px, Py
transformacja przez podobieństwo (konforemna) transformacja Helmerta - zachowuje kąty w skali. Mamy do wyznaczenia 4 wsp, które opisują nam model korekcji tak, że musimy mieć 2 znaczki tłowe z pomierzonymi wsp tłowymi z uwzględnieniem kalibracji kamery. Możemy wtedy ułożyć 4 równania obserwacyjne rozwiązać je metodą podstawienia i wyznaczyć niewiadome: a0, b0, a, b. Zakładamy tu, że: osie układu są ortogonalne, zniekształcenia skali wzdłuż obu osi są jednakowe (2 pkt dostosowania)
Po bazie
Poprawne ułożenie negatywów lub diapozytywów na płytce szklanej (nośniki zdjęć), krzyżyki wyznaczają środki obrotów - punkty główne zdjęć
Za pomocą pokrętła x i y sprowadzamy lewy znaczek pomiarowy na pkt główny lewego zdjęcia
Posługując się pokrętłami x, p, q naprowadzamy znaczek pomiarowy na pkt główny prawego zdjęcia (wtedy ucieka lewy pkt główny)
Pokrętłem x naprowadzamy lewy znaczek pomiarowy na lewy pkt główny
Pokrętłem p w polu widzenia okularu naprowadzamy szczegół sytuacyjny
Po znaczkach tłowych
Pokrętłami x i y naprowadzamy lewy znaczek pomiarowy na pkt główny lewego zdjęcia
Pokrętłem x naprowadzamy znaczek tłowy nr 6 lub 8, widoczną paralaksę usuwamy pokrętłem (kappa)
Kontrolę poprawności orientacji przez powrót na lewy pkt główny
Wszystkie czynności powtarzamy dla prawego zdjęcia wykorzystując tylko prawą część układu optycznego.
w punkcie a usuwa się paralaksę py przesuwem by''
1 - obrót κ''
4 - przesunięcie bz'' [ωL, φL, κL]
3 - obrót φ''
6 - nadkorekcja paralaksy obrotem ω''
powtórka czynności od 1 - 5 dopóki paralaksa nie zniknie na 5 punktach orientacji
kontrolę orientacji przeprowadza się punktem 5. Jeżeli występuje tam paralaksa tzn że nie usunięto jej dokładnie na poprzednich punktach.
Pozwala zagęścić osnowę geodezyjną fotogrametryczną na podstawie osnów III klasy i osnów pomiarowych,
Informacje o terenie w zbiorze danych (nr punktu, X, Y, Z)
Pozwala stworzyć zbiór informacji o terenie w postaci numerycznej,
Kody punktów, numery, X, Y (Z - jeżeli rzeźba terenu)
Autografy analogowe ze wspomaganiem komputerowym
Wykonanie numerycznej mapy syt - wys techniką fotogrametryczną
Informacje w postaci kodu punktów, numerów, wektorów
Stacje cyfrowe
Wykonanie mapy fotograf. w warstwie sytuacyjnej
Informacje o terenie w postaci obr. rastrowego przetwarzane zdjęcie z rzutu środkowego do ortogonalnego. Jest to informacja dwuwymiarowa. Ta mapa ma dodatkowe informacje (np. ilość kondygnacji budynku, jego przeznaczenie, z jakich materiałów są wykonane jego ścieny)
analityczne (stereokomparatory precyzyjne)
cyfrowe (stacje cyfrowe)
metody analogowe (aytografy analogowe z numeryczną rejestracją na wyjściu)
metody analityczne
ze znanych lub przyjętych dla pierwszego zdjęcia obrotów tworzymy macierz obrotów A i określamy następujące wielkości x', y', z', współrzędne wektora r'.
wybieramy wartości przybliżone dla drugiego zdjęcia 1by, 1bz, 1φ'', 1ω'', 1χ''.
obliczamy wartości 1x', 1y', 1z' za pomocą wartości z punktu 2.
obliczamy niewiadome dφ, dω, dχ, dbz, dby przez rozwiązanie minimum 5 równań.
obliczamy elementy pierwszej poprawionej macierzy 2A posługując się elementami obliczonymi w punkcie 4.
obliczamy macierz A=2A*1A. Elementy tej macierzy posłużą do obliczeń jak w punkcie 3.
powtarzamy obliczenia od punktu 3 do 6 dopóki dφ, dω, dχ, dbz, dby nie staną się dostatecznie małe aby je pominąć.
kąta rozwarcia kamery fotogrametrycznej
skali zdjęć
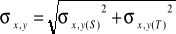
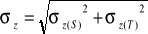
najdokładniejsze są pokrywy kanałów studzienki /4-6 cm(x,y), 1-3 cm(z)/,
mniej dokładne są narożniki budynku, płoty /x,y - 7-12 cm, z - 8-15 cm/,
tereny rolne- narożniki pól /x,y- 20-100 cm, z- 10-20 cm/,
pojedyncze krzaki, drzewa / x,y- 20-100 cm, z- 20-100 cm/
modele są przesunięte, odwrócone i zniekształcone,
modelem matematycznym rozwiązania jest przestrzenna trassformacja,
dokładności gorsz niż w metodzie wiązek (plus: jest to metoda etapowa /sekwencyjna/ - 1. orientacja wzajemna, 2. budowa pojedynczego modelu, 3. orientacja bezwzględna; umożliwia rozłączenie wyrównania sieci płaskiej i wysokościowej; minus: występuje problem dołączenia kolejnych modeli).
naturalna sygnalizacja (do opracowań map średnio i małoskalowych)
sygnalizowane sztucznie - przed nalotem
skali zdjęć
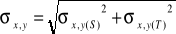
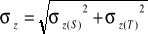
2D opracowanie
mierzymy współrzędne tłowe (x', y')
na ich podstawie i fotopunktów (min 4) wyznaczamy współrzędne X, Y w terenie
3D opracowanie np. aerotriangulacji
co najmniej 2 zdjęcia,
mierzymy na nich x', y', x'', y'',
musimy mieć też min 3 fotopunkty otrzymujemy X, Y, Z terenowe (geodezyjne)
istnieje możliwość dołączenia obserwacji geodezyjnych (np. pomierzonych długości między fotopunktami, obserwacji różnic wysokości, pomierzone azymuty, pomierzone kierunki) co czyni układ równań lepiej rozwiązywalnym,
można przyjąć do wyrównania obserwacje fikcyjne np. obserwacje zbiornika wodnego, przyjmujemy że powierzchnia wody jest w każdym punkcie taka sama,
możemy też wprowadzić dodatkowe parametry opisujące błędy systematyczne zdjęcia (dystorsja radialna, tangencjalna, deformacja negatywu). Można je opisać w postaci wielomianu
najdokładniejsza metoda rozwiązania aerotriangulacji dzięki temu, że zachodzi bezpośredni związek między współrzędnymi zdjęcia a współrzędnymi geodezyjnymi, wyrównanie przez równanie kolinearności (nie ma konieczności rozwiązania pojedynczego modelu jako etapu obliczeń)
jest możliwość wprowadzenia dodatkowych obserwacji geodezyjnych,
możliwość prowadzenia obserwacji GPS dla EOZ,
wprowadzenie obserwacji fikcyjnych (obserwacje np. punkty leżące na jednej prostej - linia przesyłowa wysokiego napięcia na wybranym odcinku),
możemy wprowadzić parametry dodatkowe opisujące błędy systematyczne kamery????????????????????????,
pozwala wyznaczyć obraz rastrowy dla autografów analitycznych i cyfrowych (bo otrzymujemy EOZ zdjęć),
pozwala rozwiązać zdjęcia o niekonwencjonalnych orientacjach
optyczno - mechaniczne urządzenie systemu projekcji,
komputer sterujący,
komputer aplikacyjny - funkcja kreślenia,
2 wózki, nośniki zdjęć,
komputer sterujący (transformacja w czasie rzeczywistym z układu współrzędnych zdjęcia do układu współrzędnych modelu - transformacja m' x(X) numeryczna
48. RODZAJE EFEKTU STEREOSKOPOWEGO
W zależności od ułożenia zdjęć względem siebie może być uzyskany jeden z trzech rodzajów efektu stereoskopowego:
- efekt ortoskopowy - przy którym model utworzony z pary zdjęć lotniczych ma ukształtowanie pionowe zgodne z naturalnym tzn. wzniesienia terenowe są skierowane w stronę obserwatora. Bazy fotografowania zajmuje położenie „do wewnątrz”.
- efekt pseudoskopowy - przy którym następuje zmiana ukształtowania pionowego, tzn. formy wypukłe obserwyje się jako wklęsłe, rzeki płyną grzbietami itp. Powstaje na skutek obserwacji zdjęcia lewego prawym okiem, a prawego lewym. Baza fotografowania na zdjęciach zajmuje położenie „na zewnątrz”.
- efekt zerowy - (minimalny), przy którym zanika wrażenie plastyki. Teren płaski. Zdjęcie lewe skręcone jest o 90o i obserwowane lewym okiem, a prawe jest także skręcone o 90o i obserwowane prawym okiem. Efekt zerowy stosowany jest wtedy, gdy przy obserwowaniu stereogramu niepożądana jest obserwacja przestrzennego ukształtowania terenu.
49. WIRTUALNY ZNACZEK POMIAROWY
Sposób pomiaru za pomocą znaczka wirtualnego nazywany jest także sposobem dwóch znaczków rzeczywistych wyobrażalnego. Ogólną zasadą pomiaru stereoskopowego za pomocą dwóch znaczków wyjaśnia rysunek. Jeżeli w polu widzenia każdego zdjęcia umieścimy znaczek pomiarowy, którego położenie względem zdjęcia może się zmieniać, to istnieje takie jedno położenie znaczka, przy którym jest on styczny do powierzchni modelu.
W położeniu wyjściowym - stosunkowo łatwo jest monokularne pokrycie jednego znaczka pomiarowego z obserwowanym punktem, np. a'. Równocześnie z tym drugi znaczek przemieszczany jest w płaszczyźnie drugiego zdjęcia (π2). Jeżeli ustawienie drugiego znaczka odpowiada położeniu 3, to przestrzenny znaczek pomiarowy znajdzie się pod powierzchnią widocznego modelu stereoskopowego. Dopiero dokładne naprowadzenie prawego znaczka na punkt a'' zdjęcia π2 - położenie 1 - prowadzi do styczności wyobrażalnego znaczka pomiarowego z mierzonym punktem A modelu. Doprowadzenie do styczności wyobrażalnego znaczka pomiarowego z obserwowanym punktem modelu, osiągnięte więc jest poprzez dokładne naprowadzenie znaczków rzeczywistych na jednoimienne punkty zdjęć π1 i π2. następnie na licznikach instrumentu wykonywane są odczyty położenia punktów na zdjęciach.
Wartość odczytu odpowiadającego położeniu znaczka pomiarowego na danym punkcie zdjęć jest funkcją tego punktu na powierzchni modelu stereoskopowego od bazy obserwacji.
50. INSTRUMENTY DO UPROSZCZONYCH OPRACOWAŃ STEREOFOTOGRAMETRYCZNYCH - STEREOSKOP ZWIERCIADLANY I STEREMIKROMETR.
Stereoskop zwierciadlany składa się z dwóch par luster, które ustawione są w stosunku do obserwowanych zdjęć pod kątem 45˚. Promienie biegnące od lewego zdjęcia widziane są jedynie lewym okiem, a promienie biegnące od prawego zdjęcia prawym okiem. Jeżeli obserwacje prowadzone są w płaszczyznach rdzennych, to obserwator odbiera efekt stereoskopowy modelu A, L, C. Model ten powstaje na przecięciach się przedłużeń promieni, jednoimiennych punktów, wpadających do oczu obserwatora. Baza obserwacji b0 zostaje powiększona do wielkości nb0, dzięki zastosowaniu rozstawionych zwierciadeł. W niektórych typach stereoskopów, oprócz zwierciadeł, umieszczone są także soczewki albo lunetki, których zadaniem jest dodatkowe powiększenie obrazu.
Stereomikrometr - śruba pararalaktyczna za pomocą, której mierzy się różnice paralaks. Składa się z 2 identycznych znaczków pomiarowych na płytkach szklanych, które ułożone na zdjęciu pod stereoskopem umożliwiają - za pomocą mikrometru - pomiar różnic paralaks.
51
52. ZALEŻNOŚCI PRZEWYŻSZENIA OD PARALAKS PODŁUŻNYCH NA ZDJĘCIACH ŚCIŚLE PIONOWYCH.
hD - jest znane
Δh = hE - hD
B - baza
PD - paralaksa punktu D
PE - paralaksa punktu E
H-hD = B*CK/PD hD = H - B*CK/PD
H-hE = B*CK/PE hE = H - B*CK/PE
Δh = hE - hD = B*CK/PE - B*CK/PD = (BCK(PE - PD))/( PE * PD)
![]()
oznaczając PD = b' = b'' = b b'-baza w skali zdjęcia b'= Ol'Op'' b''= Ol''Op'
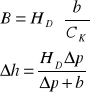
53 STEREOKOMPARATORY - STEKOMETR 1818 I STEREOKOMPARATOR PRECYZYJNY STECOMETR C
„książka stereofotogrametria lotnicza2”M. Graliński str 39-46
stereokomparator- urządzenie do pomiaru współrzędnych tłowych lub paralaks stereogramu. Do pomiaru przyjnuje się równoległe pary zdjęć; układ odniesienia to oś „x” lub oś „y”, doprowadzany poziomą łącznicą lewego i prawego zdjęcia do równoległości z osią x stereokoparatora (lub pionową łącznicą do równoległości z osią y streokomp.).
Steco 1818
budowa: żeliwna rama z prowadnicami, po której przesuwa się wózek, licznik ze śrubą, zacisk dokujący, śruba „q” - do ustawiania paralaksy poprzecznej, „p”-paralaksy podłużnej, okulary, układ optyczny, włącznik oświetlenia.
Stecometr C
budowa: komputer, urządzenie do odczytu i transmisji danych, jednostka centralna: okulary o dużym powiększeniu, nośniki zdjęć na wózkach, korbki powodujące przesunięcie obydwu zdjęć (ruch „x”, lub ruchomych części układu optycznego - ruch „y”; korbki nośników zdjęcia prawego [Px=p] /prawe porusza się wzglllędem lewego/; korbki nośników zdjęci lewego [Py=q] /lewe porusza się wzglllędem prawego/) , 6 różnych znaczków pomiarowych.
54. CYFROWE EKRANOWE MONO I STEREOKOMPARATORY
VSD (videostereodigitizer) - cyfrowy autograf analityczny, może pracować jako monokomparator i jako stereokomparator. Pomiar odbywa się na ekranie monitora za pomocą znaczka pomiarowego (sterowanego myszą)
POPOS -dokładność porównywalna z dokładnością stereokomparatorów prewcyzyjnych rzędu ok. 0,1-0,3 piksela, monitor + odpowiednie oprogramowanie
55
56 REDUKCJA WSPÓŁRZĘDNYCH TŁOWYCH ZDJĘCIA I PIKSELOWYCH OBRAZU
x0,y0 - określa położenie środka rzutów w stosunku do układy współrzędnych tłowych na zdjęciu
(rys) xa = xa' - x0,
w procesie transformacji afinicznej dokonuje się redukcji współrzędnych tłowych i korekcja błędów systematycznych (min. 3 pkt dostosowania, najpierw odległość wsp. transformowanych, potem przeliczane są współrzędne)
(rys) przejście z układu pxl. do tłowego x' = (X' - Xp') px
x' = (Y' - Yp') py
Transformacja pomierzonych wsp pixelowych do układu wsp tłowych za pomocą transformacji afinicznej w VSD
Metody transformacji wsp tłowych zdjęcia i pxl obrazu
Deformacje spowodowane są tym, że nie zachowana jest oś odciętych, rzędnych przy skanerze. Otrzymujemy układ z nieprostopadłymi osiami, wówczas trzeba stosować transformacje, które powodują:
- redukcję układu
- wprowadzenie korekcji deformacji ze względu na błędy systematyczne podłoża fotograficznego (najczęstszym źródłem błędów systematycznych jest niedociskanie materiału fotograficznego w momencie ekspozycji oraz zniekształcenie spowodowane jego obróbką i przechowywaniem)
- największa jest deformacja materiału negatywowego
- błędy szczególne układu optycznego kamery fotograficznej (deformacja radialna i tangencjalna)
Do wprowadzenia korekcji systematycznych błędów wsp tłowych stosuje się następujące transformacje, które przekształcają pomierzone wsp tłowe na układ wsp wzorcowych
Sytuacja: mamy 4 znaczki tłowe i obserwując wsp tłowe jesteśmy w stanie ułożyć 8 równań:
x' = a0 + a1xs' - b1ys'
y' = b0 + b1xs' - a1ys' xs', ys' - w układzie stereokomparatora
2. pseudoafiniczna (bilinearna) - musimy wyznaczyć współczynnik, stąd potrzeba 4 znaczków tłowych. Stosowanie metod ścisłych jest utrudniona, ponieważ brak tu obs nadliczbowych, tzn układ równań jest słabo określony. Transformacja ta nie powinna być stosowana w przypadku kamer z 4 znaczkami tłowymi, jajlepiej stosować ją dla kamer semimetrycznych ... ponieważ tutaj jest dużo obs nadliczbowych.
x' = a0 +a1xs' + a2ys' + a3xs'ys'
y' = b0 + b1xs' + b2ys' + b3xs'ys'
3. afiniczna - zakłada wyznaczenie 6 współrzędnych opisujących ten model transformacji. Musimy tu mieć 3 znaczki tłowe i na ich podstawie ułożyć 6 równań poprawek dla współczynnika. Dzięki niej można obliczyć mx, my (wsp zmiany skali wzdłuż osi) oraz kąty między osiami układu. Metoda uwzględnia nieprostopadłość osi układu i różnoskalowe zniekształcenia wzdłuż osi układu wsp. Mimo że nie zachowuje kształtu, linie równoległe po transformacji pozostają równoległe. Oprócz poprawienia skurczu za pomocą wsp skalujących, transformacja poprawia również przesunięcie początku układu współrzędnych z układu wsp komparatora xs, ys do układu wsp tłowych zdjęcia x, y oraz stosuje obrót o kat skręcenia obydwu układów.
x' = a0 +a1xs' + a2ys' + a3xs'ys' => x' = x0 + Rx'
y' = b0 + b1xs' + b2ys' + b3xs'ys'
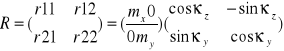
Etapy:
I - określenie wsp a i b wykorzystując pkt, które znane są w obydwu układach
II - przeliczenie wszystkich pkt z układu xs, ys na układ x, y wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać 2 równania typu (wyżej) dla każdego znaczka tłowego, czyli dla 4 znaczków tłowych 4 równania Mz współrzędnych x i 4 dla y. Dla określenia współczynnika a potrzeba tylko 3 równań dla wsp x, podobnie jak dla współczynnika b wystarczają 3 równania Mz wsp y. Dlatego równoczesne rozwiązanie tych równań met najmniejszych kwadratów zwiększa dokładność wyznaczanych niewiadomych.
57. Warunek kolinearności
Zdjęcie w położeniu pozytywowym
Wektor rb - wektor obrazowy wychodzący ze stanowiska naświetlenia zdjęcia O do pkt obrazu b
Wektor Rb - wektor przedmiotowy wychodzący ze stanowiska środka rzutów O do pkt przedmiotu B
Wektory te są kolinearne tzn jeden jest skalarny wielokrotnością drugiego, zatem rb = kRB i punkt przedmiotu B, środek rzutów O i pkt obrazu b leżą na jednej prostej. Warunek ten może być zakłócony, gdyż zniekształcenie obrazu spowodowane dystorsją obiektywu, refrakcją atm itp mogą spowodować odchylenie promienia od kolinearności - można je wyeliminować za pomocą poprawek
58. ANALITYCZNE WYZNACZENIE EOZ ZDJĘCIA - x0, y0, z0, ω, φ, κ
a) Wyznaczenie EOZ na podstawie przekształcenia rzutowego na podstawie odpowiednich wzorów , mając 8 pkt oraz interpretacyjnie
b) z warunku kolinearności (wcięcie wstecz) We wzorach warunku kolinearności występuje 9 niewiadomych x0, y0, Ck, Xs, Ys, fs, ω, φ, κ (5 fotopunktów) lub jeśli znane są EOW (3 F)
Jeśli EOW są znane i przyjmujemy przybliżone wartości EOZ i poprawki do nich to mając obserwacje nadliczbowe można ułożyć równania poprawek ( ) macierzowo w postaci V=AX-L L-macierz wartości stałych MIN. V - macierz poprawek wsp tłowych, A- macierz współczynników mij występujących przy niewiadomych.
Rozwiązanie układu równań metodą iteracyjną x - macierz niewiadomych poprawek do przyjmowania na początku wartości przybliżonych.
c) Przestrzenne wcięcie wstecz do wyznaczenia Xs, Ys, Zs mając 3 Fotopunkty. Porównuje się kąty α, β, γ określone odpowiednio równaniami zawarte między kierunkami do F pkt-ów w przestrzeni przedmiotowej i ich obrazów na zdjęciu . .. w przestrzeni obrazowej. Przyjmuje się przybliżone wartości Xs, Ys, Zs i iteracyjnie wyznacza poprawki do nich (dopóki poprawki nie staną się bliskie 0)
58A METODY ORIENTACJI ZDJĘĆ NA STEREOKOMPARATORACH
59. PARA ZDJĘĆ. ELEMENTY ORIENTACJI WZAJEMNEJPARYZDJĘĆ:
Δφ - różnica między kątami nachylenia podłużnego, określona w płaszczyźnie x2z2
Δω - różnica między kątami nachylenia poprzecznego, określona w płaszczyźnie y2f
Δκ - różnica między kątami skręcenia, określona w płaszczyźnie drugiego zdjęcia π''
![]()
Kąt nachylenia bazy względem przyjętego układu odniesienia ( oś pierwszego zdjęcia pionowa zatem płaszczyzna x1y1 pozioma )
![]()
Kąt zwrotu bazy w stosunku do przyjętego układu x1y1z1 dla pierwszego zdjęcia
60. WYZNACZENIE ELEMENTÓW ORIENTACJI WZAJEMNEJ- PRZYPADEK NIEZALEŻNEJ I ZALEŻNEJ PARY ZDJĘĆ
I) niezależna orientacja wzajemna przeprowadzana sposobem kolejnych przybliżeń wykorzystuje 6 pkt rozmieszczonych standardowo. Punkty te nazywane są punktami orientacji - pkt 1 i 2 są rzutami pkt lewego i prawego zdjęcia, a pkt 3, 4, 5, 6 leżą w czterech narożach modelu stereoskopowego w jednakowej odległości na prostych prostopadłych do łączącej punkty 1 i 2 (bazy modelu)
1) czynności przygotowawcze
2) usunięcie paralaksy podłużnej - zmianą wysokości ekranu stolika
3) eliminuje się paralaksę poprzeczną: - usuwa się paralaksę py w pkt 1 obrotem κ'' prawego projektora
- usuwa się paralaksę py w pkt 2 obrotem κ' lewego projektora
- usuwa się paralaksę py w pkt 3 obrotem φ'' prawego projektora
- usuwa się paralaksę py w pkt 4 obrotem φ' lewego projektora
- wprowadza się połowę występującej w pkt 5 lub 6 paralaksy py w kierunku przeciwnym jej występowaniu obrotem ω któregokolwiek projektora
- powtarza się czynności wyżej wymienione dopóki nie zostanie usunięta całkowicie paralaksa na tych 5 punktach. Szósty punkt służy do kontroli poprawności wykonania orientacji wzajemnej.
II) Zależna orientacja wzajemna jest wykorzystywana wtedy, gdy jeden z projektorów nie może zmieniać swojego położenia. Wówczas wykorzystuje się przesunięcia i obroty ω, φ, κ, by i bz tylko drugiego projektora. Najpierw dokonuje się eliminacji px, a później py. Jeżeli lewy projektor ma zostać nienaruszony, to kolejność eliminacji jest następująca:
Znając wartości pomierzonych paralaks py w sześciu punktach można ułożyć 6 równań dla 5 elementów orientacji, które zostaną wykorzystane do ustawienia na podziałkach autografu. Po ustawieniu obliczonych wartości na przyrządzie dokonuje się ponownego pomiaru paralaks i obliczeń poprawek do elementów orientacji.
61. WARUNEK KOMPLAMARNOŚCI
Dwa środki rzutów O1 i O2, pkt przedmiotu A oraz dwa obrazy tego punktu a' i a'' na zdjęciu stereogramu leżą na wspólnej płaszczyźnie - jest to podstawowy warunek orientacji wzajemnej i fotogrametrycznego wcięcia w przód. Warunek ten określa funkcja Fi, która jest iloczynem mieszanym trzech wektorów Fi = B R1i x R2i = 0
Jedno równanie określające komplemarność trzech wektorów B, R1, R2 można zapisać dla każdego punktu przedmiotu.
(rys)
62. PRZYBLIŻONA METODA WYZNACZENIA ELEMENTÓW ORIENTACJI WZAJEMNEJ.
Zakłada się tu że każdy z fotogramów tworzących stereogram jest wychylony o wartości kątowe EOZ ωL, φL, κL, oraz ωP, φP, κP. Tworzy się układ równań dla 6 pkt standardowych znajdujących się na obszarze podwójnego pokrycia. Metodę tę stosuje się dla układu definiowanego przez poziomą bazę, czyli gdy para zdjęć jest niezależna.
Wychodząc z ogólnego równania poprawek, dzięki temu że możemy ustawić współrzędne dla punktów standardowych, równanie upraszcza się . Poprzez kolejne redukcje możemy wyznaczyć EO wzajemnej, ale tylko kątowe.
Metody tej nie stosuje się do wyrafinowanych procedur analityczno-numerycznych. Stosuje się ją, gdy np. wykonujemy pracę na autografie i aby przyspieszyć proces strojenia, gdy pomierzymy paralaksę i ze wzorów wyliczymy EO wzajemnej.
62. Analityczne wyznaczenie elementów orientacji wzajemnej metodą przybliżoną
Zakłada się tu że każdy z fotogramów tworzących stereogram jest wychylony o wartości kątowe EOZ ωL, φL, κL, oraz ωP, φP, κP. Tworzy się układ równań dla 6 pkt standardowych znajdujących się na obszarze podwójnego pokrycia. Metodę tę stosuje się dla układu definiowanego przez poziomą bazę, czyli gdy para zdjęć jest niezależna.
Wychodząc z ogólnego równania poprawek, dzięki temu że możemy ustawić współrzędne dla punktów standardowych, równanie upraszcza się . Poprzez kolejne redukcje możemy wyznaczyć EO wzajemnej, ale tylko kątowe.
Metody tej nie stosuje się do wyrafinowanych procedur analityczno-numerycznych. Stosuje się ją, gdy np. wykonujemy pracę na autografie i aby przyspieszyć proces strojenia, gdy pomierzymy paralaksę i ze wzorów wyliczymy EO wzajemnej.
sieć triangulacyjną budujemy jednocześnie ze wszystkich zdjęć szeregu lub bloku. Dla każdego punktu o pomierzonych współrzędnych tłowych układa się po 2 równania wiążące te współrzędne ze współrzędnymi terenowymi danego punktu który jest odfotografowany na min 2 kolejnych zdjęciach np. jeżeli 1 punkt wiążący odfotografowuje się na 3 kolejnych zdjęciach szeregu to mamy 2*3=6 równań kolinearności i więcej jeśli ten punkt jeżeli ten punkt odfotografowuje się na zdjęciach z sąsiedniego szeregu.
Tworzenie aerotriangulacji
Technologie fotogrametryczne stosowane do pozyskiwania danych zasilających systemy:
1. Aerotriangulacja
2. Opracowanie NMT
3. Stereodigitalizacja (numeryczna mapa syt - wys)
4. Ortofotografia cyfrowa (ortofotomapa cyfrowa) reprezentowana przez raster
Metody:
terrotriangulacja - gdy zagęszczenie na podstawie zdjęć naziemnych, dla obiektu inżynierskiego (np. zapora, most)
Kategorie równań poprawek
I. Budowa pojedyńczego modelu polega na wyznaczeniu EOZ
Linie wersorów tworzą wiążkę stąd metoda wiązek (metoda budowy modelu metoda Schmida) - metoda matematyczna.
Metoda wiązek opiera się na warunku kolinearności. Równania poprawek układane dla wielkości tłowych (x', y') bezpośrednio obserwowanych
1. Fotopunkty bezbłędne
- np. przy wcięciu przestrzennym wstecz
2. Fotopunkty obarczone błędami
3. Punkty wyznaczane przy niewiadomych dla EOZ i punktów wyznaczanych mają te same bezwzględne wartośic.
II. Sposób niezależnych modeli.
III. Sposób odnoszący się do niezależnego wyrównania płaskiego (x, y) i wysokościowego (z) sposobem wielomianów.
Aerotriangulacja metodami analitycznymi, która pozwala na podstawienie obserwacji fotogrametrycznych (współrzędne tłowe) i obserwacji geodezyjnych (współrzędne fotopunktów) wyznaczyć na drodze zależności matematycznej współrzędnych przestrzennych X, Y w układzie terenowym.
Metody aerotriangulacji analitycznej
MW |
MNW |
1) podstawą jest warunek kolinearności metoda Schmida 2) pojedyncze zdjęcie musi mieć wyznaczone X, Y, Z, φ, ω, χ (dla 1 zdjęcia EOZ) i x', y', φ', ω', χ', x'', y'', φ'', ω'', χ'' (dla dwóch zdjęć) w metodzie wiązek 2 pełne i 1 Z-fotopunkt. Mamy jeden 1 model 4 fotopunkty pełne - równanie poprawek w metodzie wiązek dla każdego punktu mierzymy x', y', x'', y'' w pasie podwójnego pokrycia pkt. 50 50*2*2zdj = 200 równań poprawek - Dla uproszczenia wprowadza się quasiobserwacje 4*3 = 12+200=212 liczba niewiadomych 2*6=12 3*50=150 162 metoda wiązek - liczymy iteracyjnie, wyznaczone w iteracjach przyrosty do niewiadomych, suma przyrostów z koleinych iteracji daje ostateczną wartość niewiadomych. |
1) podstawą jest warunek komplanarności na podstawie którego wyznaczamy EOWzajemnej Metoda etapowo - sekwencyjna - w I etapie wyznaczamy φ'', ω'', χ'', by, bx, Δφ, Δω, Δχ - później pomiar współrzędnych modelu - w III etapie wyznaczenie EOBezwzględnej (7) X0, Y0, Z0, m, Ω, Φ, Κ 5+7=12 Warunek wyznaczenia EOBz - 2 pełne fotopunkty o współrzędnych (X, Y, Z) i 1 Z-fotopunkt o współrzęnych Z. Fotopunkty umieszczone są w pasie podwójnego pokrycia. 1. EOBz (5) ile punktów należy pomierzyć dla wyznaczenia EOBz 9-12 punktów, dla 12 punktów 12 równań poprawek do wyznaczeni 5 niewiadomych w I etapie mierzymy x', y', x'', y''. Mamy 200 obserwacji do wyznaczenia 200 punktów modelu 3*4= równań poprawek każdy fotopunkt 3 równania poprawek |
63. ŚCISŁA METODA WYZNACZANIA ELEMENTÓW ORIENTACJI WZAJEMNEJ - METODA SCHUTA
Metodę tę stosuje się, gdy układ zdefiniowany jest tu umownie (BxF')*F''=0 pozornym lewym zdjęciem. Początkowo punkty przestrzeni przedmiotowej powinny znajdować się w płaszczyznach rdzennych (komplementarności). Na początku zakładamy dla lewego zdjęcia, że φ', ω', χ' = 0, poprawki dla współrzędnych tłowych x', x'' = 0, natomiast poprawki dla y', y'' różnią się znakami, a więc redukują się. Niewiadomymi w równaniu są: by, bz i współrzędne x'', y'', z'' będące współrzędnymi promienia rzutującego r'' określonymi pomierzonymi na zdjęciu wspólrzędnymi x'', y'', CK, φ'', ω'', χ''. Dlatego poszukiwanymi niewiadomymi są: by, bz, φ'', ω'', χ''.
Kolejność obliczeń:
Pięć punktów musi być rozmieszczone jak przy punktach standardowych ze względu na pow. krytyczne gdy mamy więcej niż 5 punktów niewiadome (punkt 4) obliczamy wyrównaniem. Równanie błędów rozwiązujemy metodą najmniejszych kwadratów.
64. ORIENTACJA BEZWZGLĘDNA MODELU METODĄ TRANSFORMACJI PRZESTRZENNEJ PRZEZ PODOBIEŃSTWO
Polega ona na przetransformowaniu układu lokalnego (układu współrzędnych modelu) do układu współrzędnych terenowych. Początkiem lokalnego układu współrzędnych jest środek rzutów lewego zdjęcia a oś celowa lewego zdjęcia pokrywa się z osią układu współrzędnych. Zależność między tymi dwoma układami opisana jest wektorami. Wektor x0 opisuje odległość wektorową między układem współrzędnych geodezyjnych a środkiem rzutów układu współrzędnych modelu; wektor xS opisuje położenie punktu w układzie współrzędnych geodezyjnych, a wektor x - w układzie modelu.
Sposób zapisu wcięcia w przód: xS=x0+mRx
Otrzymujemy tu zespół równań z 7 parametrami transformacji x0, y0, z0 (składowe przesunięcia wektora translacji) elementy kątowe φ, ω, χ macierzy obrotu oraz współrzędne zmiany skali m. Może być tak, że współczynnik zmiany skali wzdłuż każdej osi jest inny (mx, my, mz) i wtedy mamy 9 niewiadomych. Aby obliczyć 7 parametrów w sposób ścisły trzeba mieć min 7 obserwacji ??????????????.
Jednak najczęściej stosuje się 3 pełne fotopunkty, z czego można ułożyć 9 równań. Układ poprawek rozwiązujemy metodą najmniejszych kwadratów i w konsekwencji otrzymujemy parametry transformacji przestrzennej. Parametry te otrzymujemy w procesie iteracyjnym. Teraz korzystając z tych równań obliczamy x, y, z, każdego punktu, który nie jest w danym modelu fotopunktem.
65
66. BUDOWA MODELU METODĄ WIĄZEK.
Pomiar wykonuje się w układzie poziomej bazy. Jest to metoda jednoczesnego wyznaczenia wszystkich niewiadomych. Muszą być znane współrzędne punktów. Im dokładniej są wyznaczone tym maleje liczba iteracji. Wyznaczamy tu elementy orientacji zewnętrznej x0, y0, z0, φ, ω, χ bazując na warunku kolinearności.
67. Technologiczne aspekty wyrównania aerotriangulacji dla bloku zdjęć - rozmieszczenie fotopunktów, wielkość i kształt bloku zdjęć, dokładność wyznaczenia współrzędnych punktów obiektu i elementów orientacji zdjęć.
Metoda Schmida - odpowiada matematycznej realizacji rzutu środkowego. Fotopunkty na obszarze bloku, (jeżeli para zdjęć to 3 fotop. tworzą trójkąt równoboczny).
Dokładność dla metody wiązek (gdy punkty obserwowane są punktami osnowy sygnalizowanej w terenie przed nalotem):
błąd wyanaczenia współrzędnych płaskich: σ'x,y =6um
σz' = 0,06 %o W-wysokość lotu (SK, WK)
σz' = 0,08 %o W (NSK)
zdjęcia w skali 1:5000
σx,y = 5000x6um
W = MzxCK 300 mm
Wielkość sygnalizowania zależy od
punkt o sygnalizacji: S-sztucznej, T-naturalnej
Dokładność dla punktów sygnalizowanych naturalnie:
Błąd długości odcinka w fotogrametrii nie zależu od długości odcinka: ![]()
Metoda niezależnych modeli
67. RODZAJE I ROZMIESZCZENIE PUNKTÓW W PROCESIE BUDOWY SZEREGU LUB BLOKU AEROTRIANGULACJI - FOTOPUNKTY, PUNKTY WIĄŻĄCE PUNKTY KONTROLNE.
Stereogram - para zdjęć umożliwia obserwacje stereoskopowe. Gdy zdjęcia są silnie zbieżne to nie można wykonywać obserwacji (kąt zbieżności > od 15˚)
Stereogram zdjęc lotniczych - położenie punktów standardowych
+3 +4
+1 +2
+5 +6
12 - baza
12=15=24=26=a' powinna być jak największa aby maksymalnie opisać obszar podwójnego pokrycia
Punkty okołostandardowe - są w obszarze (1 - 1,5 cm) wokół punktów standardowych.
Szereg zdjęć lotniczych
▲Punkty dowiązania (fotopunkty) sygnalizowane w terenie:
na obszarze lotu rozmieszczone co 2 bazy
1) Punkty wyszukiwane przed nalotem i przyjęte do geodezyjnego i fotogrametrycznego wyznaczenia (np. właz do kanału, trójmiedza, pojedynczy krzak, przecięcie dróg polnych)
punkty nawiązania - są o klasę wyżej niż punkty które wyznaczają (dla celów gospodarczych wyznaczamy osnowę III klasy wtedy punkty nawiązania są punktami II klasy)
Punkty wiążące - są w pasach potrójnego pokrycia (obszar wspólny dla 3 kolejnych zdjęć). Muszą być rozmieszczone ~ w środku, u góry i na dole pasa potrójnego pokrycia.
Punkt nowo-wyznaczany - punkty dla których wyznaczane są współrzędne X, Y, Z na drodze fotogrametrycznej ( punkty nowowyznaczanej osnowy III klasy i pomiarowej, punkty katastralne - narożniki działek, punkty sytuacyjne i wysokościowe)
Punkty masowe - były to kiedyś punkty nowowyznaczane.
Punkty kontrolne - punkty, które w procesie rozwiązania i wyrównania areotriangulacji pełnią rolę punktu kontrolnego, są traktowane jako punkty nowo wyznaczane Xgeod - Xfotogr = ∆X (Y analogicznie). Powinny być w najsłabszych miejscach bloku aerotriangulacji (2-3 daleko położone, 1-2 blisko) na obrzeżach lub w środku bloku.
Punkty pomiarowe - wszystkie punkty mierzone w bloku zdjęć fotogrametrycznych.
Punkty standardowe - do numerycznej orientacji wzajemnej pojedynczego modelu.
Technologiczne aspekty wyrównania aerotriangulacji dla bloku zdjęć - rozmieszczenie fotopunktów, wielkość i kształt bloku zdjęć, dokładność wyznaczenia współrzędnych punktów obiektu i elementów orientacji zdjęć.
Metoda Schmida - odpowiada matematycznej realizacji rzutu środkowego. Fotopunkty na obszarze bloku, (jeżeli para zdjęć to 3 fotop. tworzą trójkąt równoboczny).
Dokładność dla metody wiązek (gdy punkty obserwowane są punktami osnowy sygnalizowanej w terenie przed nalotem):
błąd wyanaczenia współrzędnych płaskich:
σ'x,y =6um
σz' = 0,06 %o W-wysokość lotu (SK, WK)
σz' = 0,08 %o W (NSK)
zdjęcia w skali 1:5000
σx,y = 5000x6um
W = MzxCK 300 mm
Wielkość sygnalizowania zależy od
- kąta rozwarcia kamery fotogrametrycznej
Dokładność dla punktów sygnalizowanych naturalnie:
- najdokładniejsze są pokrywy kanałów studzienki /4-6 cm(x,y), 1-3 cm(z)/,
- mniej dokładne są narożniki budynku, płoty /x,y - 7-12 cm, z - 8-15 cm/,
- tereny rolne- narożniki pól /x,y- 20-100 cm, z- 10-20 cm/,
- pojedyncze krzaki, drzewa / x,y- 20-100 cm, z- 20-100 cm/
Błąd długości odcinka w fotogrametrii nie zależu od długości odcinka: ![]()
Metoda niezależnych modeli
- modele są przesunięte, odwrócone i zniekształcone,
- modelem matematycznym rozwiązania jest przestrzenna trassformacja,
- dokładności gorsze niż w metodzie wiązek (plus: jest to metoda etapowa /sekwencyjna/ - 1. orientacja wzajemna, 2. budowa pojedynczego modelu, 3. orientacja bezwzględna; umożliwia rozłączenie wyrównania sieci płaskiej i wysokościowej; minus: występuje problem dołączenia kolejnych modeli).
68. PRZYGOTOWANIE DANYCH FOTOGRAMETRYCZNYCH I GEODEZYJNYCH ORAZ PRZEBIEG ROZWIĄZANIA SZEREGU AEROTRIANGULACJI METODĄ WIĄZEK - NA PRZYKŁADZIE WYRÓWNANIA PROGRAMU AEROSYS.
AeroSys służy do rozwiązania i wyrównania aerotriangulacji metodą wiązek rozwiązanie met. DLT, możliwość samokalibracji, różnych transformacji.
Parametry wejściowe to: współrzędne tłowe w układzie stereokomparatora precyzyjnie zredukowane do punktu głównego; współrzędne fotopunktów i ich dokładności; CK i poprawki kamery dotyczące dystorsji itp; współrzędne znaczków tłowych.
Na początku przygotowujemy pliki: 1. bezename.txt - ze współrzędnymi tłowymi w układzie stereokomparatora. Średnie z wielokrotnego pomiaru, 2. bezename.cal - są tu informacje o: liczbie znaczków tłowych, CK, skalibrowane współrzędne punktu głównego, współrzęne dla określenia dystorsji radialnej, 3. bezename.bdl - plik dzięki któremu program odnajdzie plik tekstowy. Zawiera on: liczbę zdjęć w szeregu, ilość kamer, CK, ilośc znaczków tłowych, 4. bezename.ctl - współrzędne fotopunktów oraz ich dokładności.
Możemy aerotriangulacje obliczyć tu automatycznie lub w sposób etapowy z podglądem. Wynikiem aerotriangulacji są: współrzędne geodezyjne wyrównane nowowyznaczanych punktów; oceny dokładnośći wyznaczenia tych punktów; EOZ; poprawki do obserwacji; wartości średnie dla x, y, z z wyłączeniem lub z włączeniem punktów nawiązania (fotopunktów).
69. AEROTRIANGULACJA METODĄ WIĄZEK
Warunki redukcji do aerotriangulacji:
- w bloku zdjęć odpowiednie punkty dowiązania (fotopunkty). Dla jakości rozwiązania warunkiem koniecznym jest posiadanie punktów nawiązania w narożnikach bloku,
- warunek pokrycia podłużnego szeregu zdjęć (ok 60%), pokrycie poprzeczne 20-30%,
- położenie punktów wiążących (3 pary punktów wiążących w strefak okołostandardowych)
Punkty nowowyznaczane:
punkty wiążące (mogą być to punkty posiłkowe i punkty zagęszczenia osnowy III klasy),
punkty sytuacyjne i wysokościowe numerycznego modelu rzeźby terenu (wyznaczenie punktów osnowy III klasy i punktów osnowy pomiarowej),
punkty sytuacyjne i wysokościowe składające się na mapę numeryczną,
punkty graniczne i punkty załamania granic i punkty określające położenie użytków.
Aerotriangulacja - służy do wyznaczenia współrzędnych przestrzennych punktów (x, y, z) na drodze analitycznej lub analityczno - numerycznej na podstawie pomierzonych na zdjęciu współrzędnych tłowych. Punkty te będą punktami zagęszczenia osnowy III klasy lub osnowy pomiarowej. Jednocześnie służy do wyznaczenia punktów dowiązania w procesie orientacji bezwzględnej modelu.
Punkty nowowyznaczane po rozwiązaniu aerotriangulacji stają się fotopunktami wykorzystywanymi w procesie opracowania zdjęć na autografach.
Na podstawie pojedynczego zdjęcia:
Cechy metody wiązek:
Minusy:
- problem nieliniowości (trzeba linearyzować równania poprawek)
- wymaga pracochłonnych metod obliczeń wartości przybliżonych dla wszystkich niewiadomych,
- jest to metoda o dużym nakładzie obliczeń,
- stanowi rozwiązanie przestrzenne, a więc nie jest możliwe rozdzielenie wyrównania sytuacyjnego i wysokościowego.
Plusy:
70. METODA WIĄZEK Z DODATKOWYMI OBSERWACJAMI I GPS
Obserwacjami dodatkowymi mogą być kąty zenitalne, azymuty, odcinki, kąty poziome, obserwacje fikcyjne, proste pionowe, poziome, dowolnie zorientowane. Można dodatkowo też ułożyć równania poprawek do liniowych i kątowych EOZ i EOW.
Równania błędów do tych obserwacji można zapisać w postaci macierzowej i dołączyć do wyrównania metodą najmniejszych kwadratów (pośredniczącą).
Można też dołączyć obserwacje GPS -> współrzędne środków rzutów zdjęć. Jednak nie są one bezbłędne, gdyż w związku z ruchem samolotu są niewielkie rozbieżności pomiędzy rzeczywistymi a rejestrowanymi współrzędnymi GPS. W związku z tym również podlegają one wyrównaniu.
Zarówno obserwacje geodezyjne jak i fotogrametryczne i GPS otrzymują odpowiednie wagi w procesie wyrównania. Obserwacje GPS do nawigacji kamery (samolotu), wyznacają środek rzutów ?????????????????
Obserwacje dodatkowe to dołączenie obserwacji z GPS
I - obserwacje fotogrametryczne - z warunku kolinearności mamy wielkości bezpośrednio obserwowane czyli 2 współrzędne tłowe każdego punktu pomiarowego.
II - obserwacje geodezyjne - obserwacje fotopunktów, pomierzone odcinki między punktami, azymuty, wysokości
71. Strategia samokalibracji - rozwiązanie aerotriangulacji metodą wiązek z dodatkowymi parametrami opisującymi błędy systematyczne.
Przy wyrównaniu aerotriangulacji metodą wiązek możemy dołączyć wektor dodatkowy parametrów opisujących EOW oraz parametry opisujące deformacje systematyczne na zdjęciu (dystorsje radialną, tangencjalną, spiralną, ∆x', ∆y', ∆CK).
Dokładność wyznaczenia współrzędnych z samokalibracją:
m'x,y = ± 3um m'z = ± 0,03 %o W(sk, wk) ± 0,04 %o W(NSK)
Bez zastosowania samokalibracji wyniki są 2x gorsze.
Technika samokalibracji w wyrównaniu bloku zdjęć.
Stosowanie samokalibracji do zdjęć lotniczych pozwala poprawić dokładność opracowania. Potrzeba tu sieci fotopunktów o dużej gęstości i dokładności. Fotopunkty muszą występować na krawędziach bloku, jak i w środku, preferowane jest duże pokrycie poprzeczne, przez co zwiększa się liczba obserwacji nadliczbowych. Jeśli wprowadzimy wielomiany n-tego rzędu ze zbyt dużą liczbą parametrów, to możemy prze parametryzować układ i wówczas spadnie dokładność. Dla każdego fotopunktu możemy otrzymać dodatkowe równanie, mierząc odległości między punktami, kąty, azymuty, obserwacje GPS.
72. AUTOGRAFY ANALITYCZNE - BUDOWA I ZASADA DZIAŁANIA.
Autografy analityczne - autografy precyzyjne, brak ograniczeń spowodowanych paramertami technicznymi instrumentu, realizowana jest projekcja numeryczna.
Budowa:
Systemy obserwacji modelu: binokularny optyczny system obserwacji przestrzennej, 2 rzeczywiste (1 przestrzenny znaczek pomiarowy).
System pomiarowy:
- wprowadzenie danych x: korby ręczne, tarcza nożna, mysz,
- A/D przetwornik (JGR, koder liniowy, tablet
73,74,75,76,77,78- brak
79. NUMERYCZNY MODEL TERENU NMT - PRZEDMIOT I ZAKRES OPRACOWANIA.
NMT - zbiór współrzędnych obrazujących powierzchnię terenu z określoną metodyką obliczeń niezbędną do przetworzenia tych danych. Zbiór wszystkich informacji tworzących NMT przechowuje się w pamięci maszyny lub na odpowiednich nośniku informacji pozwalających na wprowadzenie ich do pamięci.
Punkty, które służą do odtworzenia terenu rozmieszczone są w wybranych punktach charakterystycznych terenu albo leżą na charakterystycznych liniach terenowych (warstwicach, największego spadku, skarpach, itp.) lub też mogą znajdować się w węzłach regularnych siatek.
Na podstawie NMT można rozwiązywać następujące zadania pomiarowe:
- obliczenie wysokości z punktu o zadanym położeniu (x,y),
- obliczenie współrzędnych punktów przekrojów,
- obliczenie objętości bryły ograniczonej powierzchnią terenu i płaszczyznami o danych równaniach,
- obliczenie współrzędnych punktów przebicia powierzchni terenu przez prostą o danym równaniu,
- odliczenie współrzędnych X, Y położenia punktów na warstwicy i określać warstwice
Wyróżniamy NMT rzeźby terenu i NMT sytuacji.
80. NMT - METODA ANALITYCZNA.
Metoda pomiaru:
- regularna siatka kwadratów (oczka rostra zależą od deniwelacji terenu),
- przekroje (x lub y stałe).
Pomiar statyczny rastra i profili (np. wzdłuż określonego azymutu).
Pomiar dynamiczny: np. warstwic, profilowanie dynamiczne.
Zamierzone współrzędne poddano wyrównaniu metodą wiązek.
Interpolacja warstwic i wykreowanie NMT sytuacji dla punktów sygnalizowanych:
σ'x,y =6um
σz' = 0,06 %o W-wysokość lotu (SK, WK)
σz' = 0,08 %o W (NSK)
dochodzi błąd identyfikacji:
łącznie ![]()
![]()
szacunkowe:
pomiar dynamiczny: σz = ±0,25%o W
pomiar statyczny: σz = 0,1 - 0,15 %o W
Fotopumkty - na obrzezach lotu powinny być rozmieszczone co dwie bazy czyli co 2 szeregi. Stosuje się zasade lokalizacji ich w gniazdach. Fotopunkty zawsze zaznaczone na lewym zdjeciu. Sa to punkty osnowy drugiej klasy o znanych wsp. Geodezyjnych (x,y,z)F , P(x,y), Z
Punkty wiazace - min. 3 w pasie potrojnego pokrycia czyli min. 9 procz 1, 2, n-1, n zdjecia w szeregu. Sluzy do powiazania poszczegolnych ukladow.
Punkty nowo wyznaczane - musi być wizura miedzy nimi oraz zachowane odleglosci. Punkty osnowy geod. Widziane z gory na min. 2 kolejnych zdjeciach. Wyznaczamy tu wspol x,y,z metoda fotogrametryczna.
Punkty kontrolne - fotopunkty traktowane jako punkty nowo wyznaczane umieszcz się je w tych miejscach gdzie spodziewamy się najwiekdzych bledow, na obrzezach lub w srodku bloku
Punkty masowe - często się z nich rezygnuje i dopiero w procesie obserwacji tworzy się je wcieciami. Sa to punkty szczegolow
13
P
L
L
P
L
P
Wyszukiwarka
Podobne podstrony:
spr 2, Geodezja, rok 3, Fotogrametria i teledetekcja, sprawko nr 6 aerosys
sprawko nr5, Geodezja, rok 3, Fotogrametria i teledetekcja, sprawko nr 5 ddps
Temat4 formularz, Geodezja, semestr V, Fotogrametria i teledetekcja, Temat 2
sprawozdanie nr 8, Geodezja i szacowanie nieruchomości niestacjonarne Olszyn, RoK III, sem.IV, sem.V
Zestaw pyta˝ na egzamin z geodezji III i Fotogrametrii, Geodezja i Kartografia, III rok, Geodezja in
Opracowane pytania na koło 3 7 11 15, Budownictwo UTP, III rok, DUL stare roczniki, GEODEZJA, geodez
FOTOGRAMETRI ŚCIĄGA NA KOLOS, Fotogrametria i teledetekcja
okladnka na zeszyt, Studia-Geodezja, Rok 1, rysunek techniczny
PYTANIA NA PRiL, geodezja, rok III, Podstawy Rolnictwa i Leśnictwa
Pytania na 1 koło z PRiLu, geodezja, rok III, Podstawy Rolnictwa i Leśnictwa
praca na ryek, geodezja, rok III, Gospodarka Nieruchomościami
okładka na teczke, Studia-Geodezja, Rok 1, rysunek techniczny
na 1 koło, Geodezja, rok 3, Kartografia
zadania na ćwiczenia2, geodezja, rok I, kreska (grafika inżynierska)
pytanka na komunikacyjne www.przeklej.pl, geodezja, rok III, Geodezja inżynieryjna
2 pytania na kolo, Studia Geodezja i szacowanie nieruchomości, rok III, GI
więcej podobnych podstron