dr inż. Krzysztof Chodnikiewicz Rok akademicki: 2009 - 2010

2. Dobór silnika elektrycznego

2.1. Uwagi wstępne

2.2. Czynniki ograniczające moc silnika

2.3. Metody doboru silnika

2.1. Uwagi wstępne.

Dobór silnika powinien być poprzedzony zebraniem informacji na temat maszyny roboczej oraz warunków, w których ma być ona zainstalowana.

Informacje dotyczące maszyny dotyczą:

- rodzaju maszyny (pompa, prasa hydrauliczna, obrabiarka, itd.),

- charakteru pracy maszyny (praca ciągła, przerywana, dorywcza; definicje podano w punkcie 2.3),

- cyklu pracy (jeżeli maszyna pracuje cyklicznie),

- wymaganych obrotów silnika i ewentualnie zakresu ich zmienności,

- potrzebnej mocy silnika napędowego,

- potrzebnego momentu rozruchowego,

- potrzebnego momentu maksymalnego,

- zależności momentu oporowego od prędkości kątowej

- spodziewanego przeciążenia silnika w stosunku do warunków znamionowych,

- szczególnych wymagań związanych z pracą maszyny (np. dopuszczalny czas rozruchu)

- szczególnych wymagań, które ma spełniać silnik (np. pyłoszczelność, rodzaj zakończenia wału, wał

jednostronny, dwustronny, itp.),

- danych dotyczących silników stosowanych w istniejących maszynach takiego samego, lub

podobnego typu.

Informacje dotyczące warunków, w których maszyna ma być zainstalowana, dotyczą:

- napięcia zasilania i częstotliwości tego napięcia,

- rodzaju sieci zasilającej (jednofazowa, trójfazowa),

- warunków klimatycznych (temperatura, wilgotność),

- otoczenia (hala fabryczna, otwarta przestrzeń, kopalnia, statek, itp.).

Dobór silnika polega na określeniu typu silnika (prądu przemiennego, prądu stałego, itp.), rodzaju budowy (otwarta, zamknięta), obrotów, mocy (ewentualnie momentu), odmiany wykonania (mocowanie na łapach, mocowanie kołnierzowe), końców wału (jednostronny, dwustronny). Jeżeli silnik ma mieć zmienną prędkość obrotową, to wraz z silnikiem należy dobrać urządzenia przetwarzające i sterujące.

Trudno jest jednoznacznie odpowiedzieć na pytanie jaki typ silnika (prądu stałego lub przemiennego) należy zastosować do napędu danej maszyny lub urządzenia. Kilkadziesiąt lat temu sytuacja była klarowniejsza, gdyż jeżeli prędkość obrotowa maszyny miała być zmienna, to wybierano silnik prądu stałego. Obecnie, do maszyn o zmiennej prędkości obrotowej stosowane są zarówno silniki prądu stałego jak i przemiennego. Niekiedy o wyborze typu silnika decydują czynniki inne niż czysto techniczne, takie jak, przykładowo, tradycja i doświadczenie danej firmy. Można jednak z całą odpowiedzialnością stwierdzić, że jeżeli maszyna ma pracować ze stałą prędkością obrotową, to zastosowanie silnika prądu stałego nie ma sensu.

2.2. Czynniki ograniczające moc silnika

Moc, którą można pobrać z silnika elektrycznego ograniczają czynniki 1) mechaniczne, 2) elektromagnetyczne i 3) termiczne. Ograniczenia mechaniczne związane są z wytrzymałością elementów silnika. Pierwsze ograniczenie wytrzymałościowe dotyczy wału silnika. Jego konstruktor musi tak zwymiarować wał, aby maksymalny moment silnika powodował naprężenia skręcające wał mniejsze lub równe dopuszczalnym. Drugie ograniczenie mechaniczne jest ważne z punktu widzenia użytkownika i dotyczy siły działającej na wał silnika, prostopadłej do jego osi. Wartość tej siły jest ograniczona, gdyż powoduje ona ugięcie wału silnika, a więc zmianę szczeliny powietrznej pomiędzy wirnikiem i statorem. Zmiana tej szczeliny nie może być zbyt duża. Dopuszczalna siła obciążająca wał jest zazwyczaj podawana w katalogach silnika.

Ograniczenia elektromagnetyczne dotyczą maksymalnego momentu rozwijanego przez silnik. Można przyjąć, że maksymalny moment elektromagnetyczny silnika (zarówno prądu stałego jak i przemiennego) jest w warunkach powolnego wzrostu obciążenia 2 do 3 razy większy od momentu znamionowego. Jeżeli natomiast wzrost obciążenia trwałby bardzo krótko, to silnik może - dzięki momentowi dynamicznemu - pokonać moment obciążający większy od maksymalnego momentu elektromagnetycznego.

Na moc silnika najbardziej wpływają ograniczenia termiczne i dlatego warto poświecić im szczególną uwagę. Zacznijmy od parametrów silnika, które określa się przymiotnikiem „znamionowy”. Jest to synonim słowa „nominalny”. W przypadku urządzeń mechanicznych mówimy o nominalnym udźwigu (np. dźwigi, haki), o nominalnym nacisku (np. prasy), o nominalnym ciśnieniu (np. zbiorniki), itp. Pojęcia te wiążą się z naprężeniami, które konstruktor danego urządzenia uznał za dopuszczalne i które odpowiadają stosownym przepisom polskim i międzynarodowym. Przepisy te dotyczą w szczególności urządzeń, których działanie wiąże się z bezpieczeństwem (np. wspomniane dźwigi i haki) i określają minimalny współczynnik bezpieczeństwa tychże urządzeń.

W przypadku silników, słowo „znamionowy” (moment, moc, obroty, sprawność) określa takie warunki pracy, w których - przy temperaturze otoczenia 40⁰C - temperatura uzwojeń osiąga (lecz nie przekracza) temperaturę dopuszczalną, która zależy od klasy izolacji uzwojenia, przy czym:

- klasa izolacji B odpowiada dopuszczalnej temperaturze 130⁰C,

- klasa izolacji F - temperaturze 155⁰C,

- klasa izolacji H - temperaturze 180⁰C.

Uzwojenia silnika nagrzewają się w wyniku strat mocy (rys.2.2.1). Straty w miedzi wynikają z nagrzewania się uzwojeń i są wprost proporcjonalne do kwadratu prądu silnika. Straty w żelazie spowodowane są pętlą histerezy oraz prądami wirowymi i występują podczas magnesowania i rozmagnesowywania rdzenia prądem przemiennym. Przy częstotliwości 50 Hz rdzeń silnika jest magnesowany i rozmagnesowywany 100 razy na sekundę co, wobec pętli histerezy, powoduje zużycie energii. Prądy wirowe, też powodujące straty, są indukowane w rdzeniu przez zmienne pole magnetyczne. Zmniejszenie tych strat osiąga się wykonując rdzeń z cienkich blach. W przypadku silników zasilanych z przekształtników, straty wynikają także z niedoskonałego przebiegu napięcia w czasie: niedokładnie stałego lub niedokładnie sinusoidalnego. Niedokładność tę określa tzw. współczynnik kształtu, FF (od angielskiej nazwy form factor) definiowany jest jako stosunek wartości skutecznej do wartości średniej (półokresowej) danego przebiegu. Dla napięcia idealnie stałego FF=1, dla idealnego napięcia sinusoidalnego FF ≈ 1,11. Czym większa wartość FF, tym większe odstępstwo napięcia od idealnie stałego. Sprawność silnika wyraża się wzorem

Symbole użyte w powyższym wzorze są wyjaśnione na rys.2.2.1. Sprawność znamionowa zależy od mocy znamionowej silnika (rys.2.2.2a), a przy danej mocy znamionowej - od jego obciążenia (rys.2.2.2b). Dolny wykres na pierwszy rzut oka wygląda dziwnie, ponieważ linia osiąga poziom 100%. Prawidłowa interpretacja wykresu wymaga właściwego zrozumienia określenia Percent Full

Load Efficiency, który oznacza wyrażony w procentach stosunek sprawności przy danym obciążeniu do sprawności przy obciążeniu znamionowym.

W poniższej tablicy podano fragment katalogu z podstawowymi danymi technicznymi dotyczącymi znamionowych parametrów silników indukcyjnych.

Typ silnika	Moc		Obroty	Prąd przy		Sprawność	Współczynnik mocy	Krotność prądu rozruchowego	Krotność momentu rozruchowego	Przeciążalność	Masa
													220V	380V	η
		[kW]	[KM]	[min^-1]	[A]		[%]	[cos ]	I r /I n	M r /M n	Mmax/Mn	[kg]
2p=2 Obroty synchroniczne 3000 min^-1, 50Hz
STg 80-2i	0.55	0.75	2750	2.78	1.61	68	0.78	3.60	2.20	2.30	8.40
STg 80-2A	0.75	1.00	2800	3.39	1.96	68	0.86	4.30	2.30	2.50	9.10
STg 80-2B	1.10	1.50	2800	4.44	2.57	75	0.86	4.20	2.80	3.00	11.20
STg 90-2C	1.50	2.00	2800	6.49	3.76	73	0.83	4.50	3.40	3.70	13.90
STg 90-2D	2.20	3.00	2800	8.36	4.84	82	0.84	5.50	2.90	3.00	15.00
STg 90-2F	3.00	4.00	2800	11.60	6.70	85	0.79	5.50	3.50	3.50	18.00

Przejdźmy do zjawisk zachodzących w silniku. Ciepło, dzięki któremu w czasie dt nagrzewa się silnik, wynosi

Z doświadczenia wiadomo, że zarówno nagrzanie jak i wystudzenie dowolnego ciała wymaga określonego czasu. Charakter zmienności temperatury silnika w czasie można wyznaczyć na podstawie modelu, w którym uzwojenia silnika są zastąpione jednorodną bryłą o masie m i o małym oporze przewodzenia ciepła, do której w czasie dt zostaje doprowadzone ciepło określone zależnością podana powyzej. Cześć tego ciepła, dQ_S, pozostaje w bryle, zaś pozostała cześć, dQ₀, zostaje odprowadzona do otoczenia (rys.2.2.3), przy czym

gdzie:

c_p - ciepło właściwe w
,

- nadwyżka temperatury bryły nad temperaturą otoczenia w K,

A - powierzchnia bryły przez którą odprowadzane jest ciepło w m²,

- współczynnik przejmowania ciepła w
.

Z zasady zachowania energii wynika

czyli

(#)

Jest to równanie różniczkowe liniowe, zwyczajne o stałych współczynnikach. Rozwiązanie takiego równania jest sumą rozwiązania pełnego równania uproszczonego (jednorodnego) i rozwiązania szczególnego równania pełnego.

Równanie uproszczone

(*)

Przewidywanym rozwiązaniem tego równania jest

(**)

gdzie C jest stałą. Różniczkując otrzymuje się

(***)

Podstawiając (**) i (***) do (*) i przekształcając, można obliczyć

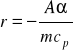
a więc rozwiązanie pełne równania uproszczonego ma postać

Łatwo sprawdzić, że rozwiązaniem szczególnym równania (#) jest

czyli pełne rozwiązanie równania (#) ma postać

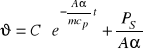
Przyjmując, że w chwili t=0 jest
uzyskuje się

i następnie

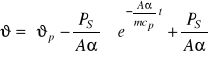
Ilorazy występujące w powyższej zależności wydają się być dość złożone. Maja one jednak prostą interpretację fizyczną. Zinterpretujmy iloraz
zakładając, że osiągnięta została ustalona nadwyżka temperatury
, czyli, że
. Z równania (#) wynika, że

czyli ostatecznie

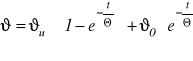
Przy czym symbolem Θ oznaczono cieplną stałą czasowa równa

Dla małych silników Θ jest rzędu kilkunastu minut, dla dużych - kilku godzin. Z ostatecznego rozwiązania wynika, że temperatura w modelowej bryle, a więc w przybliżeniu i w uzwojeniach silnika, zmienia się wykładniczo.

Polecenie

Naszkicować zależność nadwyżki temperatury
od czasu.

Polecenie

Podać interpretację fizyczna cieplnej stałej czasowej
.

Można zauważyć, że ustalona nadwyżka temperatury jest wprost proporcjonalna do mocy strat P_S. Największy udział w mocy strat przypada na straty w miedzi (rys.2.2.1), a te, jak już wiadomo, są wprost proporcjonalne do kwadratu prądu I. Z kolei, prąd jest w przybliżeniu wprost proporcjonalny do momentu silnika, M, i - dalej z coraz gorszym przybliżeniem - do mocy silnika P. Dlatego dla ustalonej nadwyżki temperatury,
, można napisać

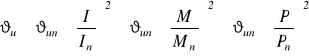
gdzie dolny indeks n oznacza znamionowe warunki pracy silnika. Z powyższych stwierdzeń wynikają metody doboru mocy silnika. Najdokładniejszą jest metoda średnich strat. Innymi metodami są: metoda prądu zastępczego, metoda momentu zastępczego i metoda mocy zastępczej.

Pytanie

Jak dla typowych silników zmienia się prąd w funkcji obciążenia?

Pytanie

Silnik jest zainstalowany na zewnątrz budynku. Czy w zimie, przy temperaturze -10⁰C. można z tego silnika uzyskac moc a) taką samą, b) większą, c) mniejszą niż w lecie?

2.3. Dobór mocy silnika

Najłatwiej jest dobrać silnik do maszyny lub urządzenia, które pracuje przez długi okres czasu przy stałym obciążeniu. Niektórzy producenci urządzeń napędzanych silnikami elektrycznymi podają w katalogach albo wprost wymaganą moc silnika, albo wymagany moment obrotowy. Na rys.2.3.1 pokazano przykładowy wykres wymaganego momentu obrotowego (napędowego) dla grupy pomp hydraulicznych. Symbole literowo-cyfrowe oznaczają typ pompy, symbole cyfrowe przy liniach - tzw. wielkość znamionową pompy. Producent informuje, że wykresy zostały wykonane dla lepkości kinetycznej 41 mm²/s i temperatury 50 ⁰C.

.

Rys.2.3.1

Pozostałe dane techniczne pomp wybrane z katalogu jako istotne z punktu widzenia doboru silnika są następujące:

Wielkość znamionowa pompy	Strumień przepływu w l/min przy 1500obr/min	Ciśnienie maksymalne w barach	Obroty minimalne obr/min	Obroty maksymalne obr/min
040	100	210	600	2500
045	89
055	80
060	66
068	59

Jeżeli osoba dobierająca silnik nie ma do dyspozycji takich informacji jak w powyższym przykładzie, to musi nie tylko dobrze znać budowę i działanie urządzenia do napędu którego dobiera silnik, ale także zachodzące w tym urządzeniu zjawiska fizyczne.

Rozróżnia się następujące rodzaje pracy silnika:

1. praca ciągła (symbol S1) - silnik pracuje pod stałym obciążeniem i osiąga ustalony przyrost (nadwyżkę) temperatury;

2. praca dorywcza (symbol S2) - silnik pracuje krócej niż to potrzebne do uzyskania ustalonej nadwyżki temperatury, a następnie zostaje wyłączony i stygnie aż do temperatury otoczenia;

3. praca przerywana (symbol S3) - silnik pracuje z przerwami, przy czym podczas pracy nie zostaje osiągnięta ustalona nadwyżka temperatury, a w okresie wyłączenia nie zostaje osiągnięta temperatura otoczenia.

Pozostałe rodzaje pracy (S4 do S8) związane są ze sposobem hamowania i rozruchu oraz biegiem jałowym, natomiast rodzaje S7 i S8 dotyczą dużej liczby załączeń.

Jak to wspomniano na zakończenie punktu 2.2, w przypadku pracy ciągłej silnik można dobrać jedna z czterech metod (średnich strat, prądu zastępczego, momentu zastępczego i mocy zastępczej).

Rozpatrzmy rys.2.3.2, na którym przedstawiono przykładowe, zmieniające się w czasie, zapotrzebowanie mocy przez maszynę. Ze wzoru definiującego sprawność wynika, że straty mocy w silniku wynoszą

czyli jeżeli silnik przekazuje maszynie moc P₁, to w tym czasie moc tracona wynosi

i podobnie dla ΔP₂ , ΔP₃ , itp.

Należy w tym miejscu zauważyć przydatność wykresów obrazujących zależność współczynnika sprawności od obciążenia takich jak pokazane na rys.2.2.2a. Wykresu te pozwalają obliczać straty mocy przy uwzględnieniu sprawności charakterystycznej dla danego obciążenia silnika. Średnie straty mocy w cyklu pracy są równe

Silnik uznaje się za dobrany prawidłowo jeżeli spełniona jest nierówność

(a)

gdzie symbol
oznacza straty w silniku obciążonym znamionowo.

Jeżeli w czasie cyklu pracy silnika występują hamowania, postoje i rozruchy, to odpowiadające im czasy występujące w mianowniku wzoru analogicznego do powyższego, należy pomnożyć przez współczynniki mniejsze od jedności, bowiem w tych okresach chłodzenie silnika pogarsza się. Jest więc

gdzie dolne indeksy R, H oraz P oznaczają odpowiednio rozruch, hamowanie i postój. Współczynniki α i β występujące w mianowniku są w przybliżeniu równe

Metoda prądu zastępczego polega na wyznaczeniu prądu I_Z , który powodowałby takie samo nagrzanie silnika jak prądy zmieniające się w cyklu pracy. Prąd zastępczy określony jest wzorem

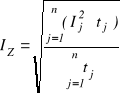
(b)

Dobór silnika uważa się za prawidłowy jeżeli spełniony jest warunek

(c)

gdzie I_n oznacza znamionowy prąd silnika.

Analogiczne do (b) wzory określają moment zastępczy i moc zastępczą, zaś nierówności analogiczne do (c) - warunki doboru silnika metodą momentu zastępczego i mocy zastępczej.

Dobór mocy silnika do pracy dorywczej i przerywanej jest nieco bardziej złożony, lecz jego istotą, tak jak w przypadku pracy ciągłej, jest analiza zjawiska nagrzewania i chłodzenia silnika.

Jeżeli dobieramy silnik do typowej maszyny, to powinniśmy znać parametry silnika zastosowanego w istniejących maszynach takiego samego lub podobnego typu.

2.4. Dobór parametrów układu silnik - kolo zamachowe

Niektóre maszyny technologiczne wykonują pracę użyteczną tylko w części cyklu roboczego. Typowym przykładem jest prasa korbowa stosowana do obróbki plastycznej metali, której suwak jest napędzany mechanizmem korbowo-wodzikowym (rys.2.4.1a). Zetknięcie stempla z obrabianym

plastycznie materiałem następuje wtedy, gdy oś A-A wykorbienia wału korbowego mija punkt Z (rys.2.4.1b). Kontakt stempla z materiałem ustaje w pobliżu dolnego zwrotnego położenia suwaka prasy. W zależności od rodzaju operacji obróbki plastycznej dzieje się to przed dojściem osi A-A do punktu K, lub też po minięciu tego punktu. Istotne jest to, że kąt α _r jest wielokrotnie mniejszy od 360⁰. Pokonanie siły reakcji kształtowanego materiału wymaga przyłożenia do wału korbowego momentu obrotowego M_k , który w przedziale odpowiadającym kątowi α _r ma dużą wartość (rys.2.4.1c). Moment obrotowy potrzebny do obrotu nieobciążonego wału korbowego, czyli poza kątem α _r , jest znacznie mniejszy. Tak obciążane maszyny korzystnie jest wyposażać w koło zamachowe (rys.2.4.1d), dzięki któremu powstaje moment dynamiczny
. (Symbolem J oznaczono moment bezwładności obracających się części układu napędowego prasy zredukowany do osi silnika, zaś symbolem ω - prędkość kątową silnika.) Gdyby koła zamachowego nie było, silnik musiałby dysponować momentem równym maksymalnej wartości momentu M_k . W czasie, w którym następuje odkształcenie plastyczne materiału, prędkość ω zmniejsza się. Następnie silnik rozpędza obracające się części układu napędowego prasy do prędkości, którą te części miały na początku odkształcania. Zmienność prędkości kątowej ω w funkcji czasu pokazano w sposób jakościowy na rys.2.4.2.

Poniżej podana będzie metoda doboru parametrów układu silnik - kolo zamachowe prasy korbowej. Schemat układu napędowego tej prasy pokazano na rys.2.4.1d. Koło zamachowe 6, ułożyskowane na wale korbowym, jest napędzane silnikiem 4 poprzez przekładnię pasową 5. Po włączeniu silnika, koło zamachowe obraca się w sposób ciągły. Włączenie sprzęgła 7 powoduje połączenie koła

zamachowego z wałem korbowym i ruch suwaka prasy, a nadto wyłączenie hamulca 8. I odwrotnie: wyłączeniu sprzęgła towarzyszy włączenie hamulca. Często od wału korbowego napędzane są urządzenia automatyzujące. W wielu prasach pomiędzy silnikiem i wałem korbowym znajduje się jeszcze jeden wał, zwany pośrednim, który napędza wał korbowy poprzez przekładnię zębatą. W prezentowanej poniżej metodzie doboru silnika i koła zamachowego liczba wałów i przekładni nie ma znaczenia, gdyż operuje się momentami zredukowanymi. Metoda może być łatwo zaadoptowana do innej prasy niż korbowa.

Warunki prawidłowego doboru parametrów układu silnik - koło zamachowe można sformułować następująco:

(a) Pomiędzy kolejnymi ruchami roboczymi suwaka silnik powinien dostarczyć energię, która umożliwi wykonanie zarówno operacji technologicznej jak i pokrycie wszystkich strat energetycznych. Straty te związane są przekazywaniem mocy przez przekładnie, biegiem luzem koła zamachowego i suwaka oraz tarciem w mechanizmach prasy podczas wykonywania operacji obróbki plastycznej. W przypadku prasy pracującej ruchem ciągłym, czas upływający pomiędzy kolejnymi ruchami roboczymi suwaka wynika z szybkobieżności prasy (porównaj rys.2.4.2).

(b) Silnik nie może być przeciążony cieplnie.

Warunki te łatwo jest sformułować słownie, trudniej wyrazić zależnościami analitycznymi. Aby te ostatnie były możliwie proste, konieczne jest wprowadzenie szeregu uproszczeń, które wynikają z dwóch przyczyn. Pierwszą jest dążenie do możliwie najprostszej formy zależności analitycznych. Przyczyna drugą, znacznie istotniejszą, jest ograniczona znajomość wielkości, które należy uwzględnić w równaniu ruchu.

Omówienie warunku (a)

W przedstawionej dalej metodzie przyjmuje się, że układ napędowy prasy może być przedstawiony schematycznie jak na rys.2.4.3, a więc opisany równaniem
- M₀ = 0

w którym symbole J i ω były już wyjaśniane, M₀ jest momentem oporowym zredukowanym do wału silnika, M_e - momentem rozwijanym przez silnik. Zakłada się, co jest uproszczeniem, że J = const oraz M₀ = const.

Rozwiązanie powyższego równania będzie dotyczyło tylko okresu rozpędzania koła zamachowego, czyli czasu pomiędzy chwilami K_t i Z_t (rys.2.4.2). Czas wyrażony odcinkiem Z_tK_t , w którym w którym materiał jest odkształcany, jest znacznie krótszy od czasu rozpędzania układu i zostanie uwzględniony w inny sposób. Dzięki temu unika się obliczeniowych komplikacji, które by wystąpiły gdyby uwzględnić skomplikowane zależności określające moment na wale korbowym potrzebny do wykonania operacji obróbki plastycznej.

W celu efektywnego rozwiązania omawianego równania należy wprowadzić do niego zależność pomiędzy momentem obrotowym M_e i prędkością kątową ω silnika. Prezentowana metoda dotyczy silnika indukcyjnego zasilanego przetwornicą częstotliwości, które to rozwiązanie umożliwia zmianę szybkobieżności prasy. Zależność M_e(ω) zależy zarówno od silnika jak i od jego sterownika (rys.2.4.4). Najczęściej naturalna charakterystyka silnika jest ograniczana linią prostą M_e = k M_n gdzie M_n jest znamionowym momentem silnika, zaś k - stałym współczynnikiem (rys.2.4.4). Wartość tego współczynnika może być programowo wybierana, najczęściej w przedziale (1,0; 2,0), przy czym fabrycznym ustawieniem jest zazwyczaj k = 1,5.

Uproszczenie dotyczące charakterystyk pokazanych na rys.2.4.4 polega na założeniu, że dla każdej częstotliwości zasilania, charakterystyka silnika składa się z dwóch prostoliniowych odcinków (rys.2.4.5). Na odcinku SC, na którym ω_C < ω < ω_S , moment silnika zmienia się liniowo zgodnie z zależnością

M_e = M_n (ω_S - ω) / (ω_S - ω_n) (*)

gdzie ω_S jest kątową prędkością synchroniczną, a ω_n kątowa prędkością znamionową, zaś dla odcinka, CD

M_e = k M_n.

Z powyższych zależności można obliczyć prędkość ω_C pisząc

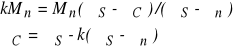
Kolejnym zadaniem na drodze do rozwiązania równania ruchu jest określenie momentu M₀. Moment ten musi uwzględniać straty energetyczne zachodzące w prasie. Straty te były już wymienione, lecz liczbowo ich nie oszacowano. Wobec braku dokładnych informacji można w tym celu wykorzystać wykres (rys.2.4.6a) zaczerpnięty z książki „Prasy mechaniczne. Konstrukcja, eksploatacja, modernizacja”, WNT, 1970r. Na rys.2.4.6b przedstawiono modyfikację wykresu źródłowego

pomijając straty w silniku oraz straty związane z działaniem sprzęgła i hamulca. Pominięcie strat w silniku wynika stąd, że w metodzie chodzi tylko o straty w prasie. Pominięcie strat związanych z działaniem sprzęgła i hamulca wynika natomiast z tego, ze metoda odnosi się do prasy automatycznej pracującej ruchem ciągłym. Jest zrozumiałe, że w przypadku przerywanego ruchu prasy, straty te powinny być uwzględnione. Zauważmy, że praca użyteczna, przy pominięciu strat w silniku oraz strat związanych z działaniem sprzęgła i hamulca, stanowi

energii dostarczonej przez silnik. Zauważmy też, że jeżeli znana jest wartość pracy użytecznej A_U, to na podstawie wykresu 2.4.6b można oszacować straty związane z biegiem luzem suwaka, koła zamachowego oraz straty w przekładni

W celu obliczenia momentu M₀ = const należy sumę
podzielić przez kąt obrotu silnika odpowiadający jednemu skokowi suwaka. Kąt ten wynosi
, gdzie symbol n_n jest znamionową liczba obrotów silnika, a n_prasy oznacza liczbę skoków suwaka prasy na minutę. Tak więc

Podstawiając M₀ do podanej na poprzedniej stronie zależności (*) uzyskuje się prędkość silnika podczas biegu luzem

ω_bl = ω_S - (M₀ / M_n)
(ω_S - ω_n)

Wykonanie operacji odkształcenia plastycznego wymaga wykonania pracy A_U + A_t. Obliczenie prędkości kątowej ω_min po wykonaniu operacji opiera się na założeniu, że praca ta wykonana zostaje tylko kosztem zmniejszenia energii kinetycznej elementów układu napędowego. Można więc napisać

-

Przekształcając, otrzymuje się

-
.

Mogą zajść dwa przypadki. W przypadku pierwszym ω_min < ω_C , w drugim ω_min > ω_C . Rozpatrzmy przypadek pierwszy. Na odcinku CD charakterystyki silnika równanie ruchu ma postać

- M₀ = 0

przy czym przyjmuje się, że w chwili t = 0 jest ω = ω_min. Rozwiązaniem tego równania jest

Rozwiązanie to obowiązuje aż do osiągnięcia przez układ prędkości ω = ω_C . Następuje to w chwili

Następnie układ „wchodzi” na odcinek CS charakterystyki, na którym równanie ruchu ma postać

To równanie można napisać jak niżej

Jego rozwiązaniem przy warunku początkowym, dla t = 0 ω = ω_C , jest

gdzie

Zauważmy, że czas liczymy „od nowa”. Jest to całkowicie dopuszczalne, należy tylko pamiętać, że wprowadziliśmy taką umowę. Czas rozpędzania układu na odcinku CS charakterystyki wynosi

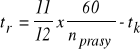
Wzór ten wynika z założenia, że czas rozpędzania na obydwu odcinkach charakterystyki wynosi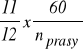
, czyli z założenia, że kąt obrotu, na którym następuje rozpędzanie równa się 330⁰ . Warto tu przypomnieć, że zgodnie z rys.2.4.2 rozpędzaniu odpowiada czas odpowiadający odcinkowi K_tZ_t .

Omówienie warunku (b)

Drugi warunek prawidłowego doboru układu silnik - koło zamachowe zastał na początku niniejszego punktu sformułowany bardzo zwięźle: silnik nie może być przeciążony cieplnie. Z punktu 2.2 wiadomo, że nadwyżka
temperatury ponad temperaturę otoczenia jest wprost proporcjonalna do kwadratu momentu rozwijanego przez silnik, czyli w naszym przypadku

(**)

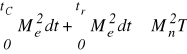
W wyrażeniu tym pierwsza całka jest wprost proporcjonalna do nadwyżki temperatury silnika powstałej na skutek pracy silnika na odcinku CD charakterystyki, zaś druga całka jest wprost proporcjonalna do nadwyżki temperatury silnika powstałej na skutek pracy silnika na odcinku CS. Wyrażenie występujące po prawej stronie jest natomiast wprost proporcjonalne do nadwyżki temperatury silnika występującej w warunkach nominalnego obciążenia, która to nadwyżka ponad temperaturę otoczenia jest całkowicie dopuszczalna. Można więc stwierdzić, że nadwyżka temperatury silnika podczas jego pracy na obydwu odcinkach charakterystyki nie może być większa od tej, która zaistniałaby gdyby silnik pracował przy obciążeniu nominalnym.

Z uwagi na to, że dla czasu t_C moment silnika jest równy kM_n , pierwsza całka wyraża się prostą zależnością

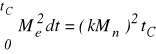
Obliczenie drugiej całki jest dość żmudne. Dociekliwy czytelnik może sprawdzić, że

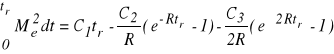
gdzie

Przytoczone zależności pozwalają sprawdzić warunek (**) i ocenić dobór parametrów układu silnik - koło zamachowe. Po ocenie można zmienić parametry i przeprowadzić ocenę jeszcze raz aż do osiągnięcia sytuacji, w której prawa strona nierówności (**) będzie tylko niewiele większa od strony lewej. Załącznikiem do kończonego już wykładu jest program napisany w Excelu, który ułatwia wykonanie zaprezentowanych wyżej obliczeń.

Zadanie:

Wyspecyfikować wszystkie uproszczenia przedstawionej wyżej metody i je krytycznie omówić.

Załącznik:

Program p.t. Załącznik do Wykładu 2009-2010 na temat doboru parametrów układu silnik-koło zamachowe

14

10

P_S - MOC STRAT:

- w miedzi,

- w żelazie (tylko silniki prądu

przemiennego)

- wentylatorowe,

- tarcia.

P_U - MOC UŻYTECZNA

MOC DOSTARCZONA

DO SILNIKA

Rys.2.2.1

Rys.2.2.2

(a)

(b)

dQ

dQ_S

dQ₀

Rys.2.2.3

0

moc P

t₁

t₂

t₃

t₄

Cykl pracy

Następny cykl

P₁

P₂

P₃

P₄

P₁

Rys.2.3.2

czas

m

9

8

7

6

5

(b)

2

(a)

α_r

1

Rys.2.4.1. (a) Mechanizm korbowo-wodzikowy: 1 - wał korbowy, 2 - korbowód, 3 - suwak; (pokazano tylko jedną prowadnicę).

(b) Tor osi A-A pokazanej na rys.(a) i kąt α _r . Jeżeli wykorbienie wału znajduje się w granicach tego kąta, to stempel styka się z odkształcanym materiałem. Kąt ten z reguły nie jest większy od 30⁰ - 40⁰.

(c) Pokazana schematycznie zmiana momentu M_k na wale korbowym prasy w funkcji czasu w przypadku pracy ciągłej. Moment M_k warunkuje pokonanie siły reakcji kształtowanego materiału; T - czas odpowiadający jednemu obrotowi wału korbowego.

(d) Schemat prasy korbowej: 1 - 3 jak na rys.(a), 4 - silnik elektryczny, 5 - przekładnia pasowa, 6 - koło zamachowe, 7 - sprzęgło, 8 - hamulec, 9 - podajnik tasmy, 10 - przyrząd.

3

4

(d)

A

A

Tor A-A

K_t

Z_t K_t

t

(c)©©

ω

K

Z

Z_t K_t

Rys.2.4.2. Zmienność prędkości kątowej silnika i koła zamachowego prasy korbowej pracującej ruchem ciągłym. Punktom Z_t odpowiada punkt Z na rys.2.4.1b,

punktom K_t - punkt K.

M_n

Czas 1 cyklu

Rys.2.4.3. Układ zastępczy zastosowany w omawianej metodzie doboru parametrów układu silnik - koło zamachowe.

(W istocie, jest to powtórzenie rys.1.2.2)

+ω +dω/dt

M_e M₀ J·dω/dt

J

S

k M_n

Prędkość kątowa ω

Moment M_e

Rys.2.4.4. Wykresy obrazujące zależność momentu silnika M_e od prędkości kątowej ω dla różnych napięć U i częstotliwości zasilania silnika f . Spełniony jest warunek U / f = const.

Moment M_e

0

0

n [obr/min]

n_n n_S

k M_n

M_n

ω [rad/s]

0

ω_C ω_n ω_S

C

Rys.2.4.5. Uproszczone charakterystyki silnika dla częstotliwości f, f₁, f₂ zastosowane w omawianej metodzie doboru parametrów układu silnik - koło zamachowe; f > f₁ > f₂.

f > f₁ > f₂

f

f₁

f₂

D

(b)

(a)

Rys.2.4.6. Bilans energetyczny typowej prasy korbowej. Na rys. (a) z uwzględnieniem strat w silniku oraz straty związane z działaniem sprzęgła i hamulca. Na rys.(b) bez uwzględnienia tych strat.

---