22. W pomiarach grawimetrycznych wykorzystuje sie różne zjawiska fizyczne, które zalezą od siły ciężkości. W zależności od sposobu pomiaru wyznacza sie:

1. Absolutna wartość przysp. siły ciężkości - pomiary bezwzględne (zawsze stosowane sa tu metody dynamiczne)

2. Różnice przysp siły ciężkości - pomiary względne (różnicowe) (zwykle stosuje sie tu metody statyczne, rzadziej metody dynamiczne).

Do metod dynamicznych pomiaru wykorzystujących ruch w polu siły ciężkości zalicza sie:

* Met. balistyczne - wyk. zależność drogi i czasu ciała spadającego w próżni z przyspieszeniem.

*Met. wahadłowe - wyk. związek okresu wahań wahadła z wartością przyspieszenia i długością ramienia

wahadła;

*Met. wykorzystujące drgania poprzeczne struny obciążonej - wyk. zależność częstotliwości drgań

struny o określonej długości i masie od wartości przysp.

W metodach statycznych sile ciężkości przeciwstawia sie sile wzorcowa (np. sprężystości gazu, sprężyny, pola magnetycznego etc.), która dazy do zachowania określonego stanu statycznego.

23. Astatyzacja polega na zwiększeniu czułości układu mierżącego poprzez wprowadzenie go w stan równowagi prawie chwiejnej ale jeszcze trwałej za pomocą przeciwdziałającej sprężyny. O wielkości wychylenia wskaźnika decyduje różnica momentów siły ciężkości i siły sprężyny pomiarowej. Czułość układu jest tym większa im mniejsza jest stabilność układu.

Grawimetry astatyzowane można rozpoznać po długim okresie drgań własnych (5-10s); nieastatyzowane maja o rząd krótszy okres drgań własnych (0.5-1s).

24. Cechowanie grawimetru (inaczej kalibracja, skalowanie lub komparacja) -czynności pomiarowo obliczeniowe, które maja na celu powiązanie wskazan grawimetru (w działkach) z jednostka przyspieszenia siły ciężkości (zwykle mGal). W wyniku cechowania otrzymuje się współczynniki równania grawimetru

Metody:

*Cechowanie na bazach graw.: do cechowania graw. statycznych zakłada się bazy:(Składające się z punktów, na których wyznaczono wartość przyspieszenia metodami absolutnymi, Poziome o przebiegu południkowym, pionowe (wykorzystujące wysokie budynki; w Polsce w PKiN))

Ponadto należy pamiętać, ze: grawimetr należy cechować przed rozpoczęciem i po zakończeniu

prac terenowych i zawsze wtedy, gdy podejrzewamy nieprawidłowa prace grawimetru.

*Grawimetry astatyzowane, w których odczytywanie odbywa się metoda zerowania mogą być cechowane przez nachylanie. Efekt wywołany nachyleniem systemu mierzącego można zapisać:

Pochylanie grawimetru zmniejsza wartość przyspieszenia, czyli daje podobny efekt jak pomiar na bazie pionowej .

25. Metodyka pomiarów grawimetrami: zależy głównie od oczekiwanej dokładności i wyróżni się 2 główne metody:

*Met. łańcuchowa: A B A B C B C D … Z Y Z (stos. w pom. o najwyższej dokładności, gdy zachodzi potrzeba

częstej kontroli dryftu grawimetru i jego uwzględnienia; zwykle w sieciach grawimetrycznych)

*Metoda profilowa: A 1 2 … n A lub B(stosowana tam gdzie odległości pomiędzy punktami pomiarowymi sa niewielkie) Odległości pomiędzy punktami bazowymi AB, BC, … nazywamy przęsłami grawimet., a odległości pomiędzy punktami pomiarowymi 1,2,… krokami pomiarowymi.

Dryftem nazywamy przesuwanie się punktu zerowego grawimetru z upływem czasu. Tzn, ze kolejne odczyty

grawimetru wykonywane na tym samym punkcie będą coraz bardziej różnic się od odczytu wyjściowego - będą

zmieniać się w czasie. Wyróżnia się dwa rodzaje dryftu: długookresowy (wynikający głównie ze starzenia się

systemu pomiarowego) i krótkookresowy (zależny od

czynników zewnętrznych). Dla wyznaczenia dryftu niezbędny jest powtórny pomiar na tym samym punkcie lub pomiar na punktach o znanej wartości przysp. Dryft wyraża średnia prędkość zmian wskazań grawimetru na jednostkę czasu).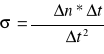

26. Redukcje grawimetryczne to pewne zabiegi rachunkowe, w których chodzi o taka zmiane wartosci przyspieszenia siły ciężkości pomierzonego na powierzchni Ziemi, aby odpowiadała ona innemu punktowi połozonemu na linii pionu stanowiska pomiarowego.

W zagadnieniach zwiazanych z teoria Stokesa (wyznaczaniem wysokosci geoidy i odchylen pionu) potrzebna jest taka wartość przyspieszenia na geoidzie, aby mozna uwazac, ze:

• masy zostały tak `przemieszczone', ze wszystkie znajduja się wewnatrz geoidy (zadne masy nie `wystaja' ponad geoide)

• całkowita masa geoidy po redukcji pozostaje równa całkowitej masie Ziemi przed redukcja

Redukcje grawimetryczne moga powodowac rózne efekty w rozmieszczeniu mas. Redukcje moga „odbywac sie”:

• z przemieszczeniem mas (np. dla celów wyznaczenia figury Ziemi)

• bez przemieszczenia mas (np. dla obliczenia wysokosci punktu w systemie wysokosci ortometrycznych)

• usunieciem mas (np. geofizyce poszukiwawczej)

Redukcje grawimetryczne obejmuja zwykle dwa podstawowe składniki (elementy):

• wpływ gradientu pionowego przyspieszenia siły ciezkosci

• wpływ (uwzględnienie) przyciągania mas o znanej lub domniemanej gęstości i rozmieszczeniu przestrzennym.

27. Poprawka terenowa w punkcie pomiarowym to wartość składowej pionowej siły ciężkości (wzieta z przeciwnym znakiem) generowanej przez otaczające go masy tworzące rzeźbę terenu. Poprawka terenowa to inaczej „rachunkowe wyrównanie” terenu wokół punktu tak, aby wartość pomierzona odnosiła sie do terenu płaskiego. Czasem stosuje sie tez redukcje topograficzna, która poza wyrównaniem terenu obejmuje również usuniecie płyty o grubości równej wysokości punktu i nieskończonym promieniu oraz przy uwzględnieniu sferycznego kształtu Ziemi.

Poprawka terenowa zawsze zwiększa wartość przyspieszenia na stanowisku pom.; zarówno usuniecie nadmiaru mas ponad stanowiskiem, jak i uzupełnienie poniżej stanowiska powoduje wzrost składowej pionowej przyspieszenia.

Z uwagi na zwykle złożona rzeźbę terenu i zróżnicowana gęstość mas wokół punktu, poprawke terenowa liczy sie sumujac niewielkie segmenty (metoda Hammera) korzystając z zależności:

Poprawkę terenowa oblicza sie uwzględniając ukształtowanie terenu wokół stanowiska w promieniu od kilkuset metrów do nawet 30 km Poprawka terenowa może osiagac znaczne wartości, szczególnie w terenach podgórskich i górzystych (np. dla szczytu Mt. Blanc wynosi +123mGal, a dla Śnieżki +24mGal).

28. Redukcja wolnopowietrzna nazywamy redukcje, która polega jedynie na usunięciu wpływu wysokości stanowiska pomiarowego ponad geoide na wartość przyspieszenia siły ciężkości.

Znak redukcji jest taki sam jak znak wysokości. Geoida w wyniku redukcji wolnopowietrznej zostanie zregularyzowna, czyli wszystkie masy znajda sie poniżej geoidy (wcześniej jednak musi być wprowadzona poprawka terenowa). Zniekształcenie geoidy w wyniku redukcji rzadko przekraczają 1 m. Redukcja wolnopowietrzna wywołuje efekt „wtłoczenia” mas pod powierzchnie geoidy, a wiec tak jakby w obszarze podpowiadającym kształtem tym masom poniżej geoidy zwiększyć gęstość.

Pewna odmiana redukcji wolnopowietrznej jest redukcja Brunsa, w której chodzi o zredukowanie zmierzonej wartosci przyspieszenia na elipsoidę ekwipotencjalna lub sferoidę normalna.

N we wzorze to wysokość geoidy względem elipsoidy ekwipotencjalnej.

Redukcja Bouguera (ze względu na płytę) nazywamy redukcje, która polega na usunięciu wpływu przyciągania płyty płasko-równoległej o stałej

gęstości σ. Zwykle przez redukcje Bouguera rozumie sie sumę poprawek topograficznej i Bouguera oraz redukcji wolnopowietrznej postaci:

Poprawka za płytę nie zmienia położenia punktu pomiarowego, a jedynie eliminuje wpływ płyty na wartosc przyspieszenia w punkcie (podobnie jak poprawka terenowa). Redukcja Bouguera regularyzuje geoide, bowiem żadne masy nie „wystają” ponad geoidę. Jednak zmniejsza całkowita masę geoidy i mocno ja deformuje.

Redukcja ta, wykorzystywana w geofizyce do poszukiwań złóż kopalin użytecznych. Wykorzystywana do interpolacji anomalii Faye'a ze względu na stosunkowo mała zależność od wysokości.

29. Redukcja Poincarego-Preya nie regularyzuje geoidy, ale tez nie zmienia jej masy. Ma na celu wyznaczenie wartości przyspieszenia siły ciężkości na geoidzie tak, aby rozkład przestrzenny mas ponad geoida nie został zmieniony. W wyniku redukcji powinniśmy otrzymać taka wartość przyspieszenia na geoidzie (lub w innym punkcie na linii pionu), jaka byśmy otrzymali z pomiaru bezpośredniego na geoidzie.

Redukcja P-P wykorzystywana jest do wyznaczenia wysokości ortometrycznych, do redukcji pomiarów wykonanych w szybach wiertniczych, czy pod powierzchnia mórz i oceanów.

Redukcja P-P mozna podzielic na 5 etapów:

1. Wprowadzenie dodatniej poprawki terenowej (+) -> uformowanie płyty

Bouguera

2. Usuniecie płyty Bouguera (-) -> wprowadzenie poprawki B.

3. Wprowadzenie redukcji wp (+) -> „zejscie” z wartością przyspieszenia na geoide

4. Przywrócenie płyty B (-) -> wprowadzeni poprawki B

5. Przywrócenie topografii terenu wokół punktu (+) -> odtworzenie przestrzennego rozkładu mas wokół punktu

31. Wys.dynamiczne. Jezeli przyjmiemy dla całej Ziemi jedna wartosc przysp. Siły ciezkosci obliczona ze wzoru na przyspieszenie normalne dla szerokosSi 45°

to otrzymamy Wzor na roznice wysokości dynamicznych 2 punktow A i B.:

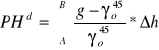
*Wys. i poprawki dynam. wyznaczane są ściśle jedynie na podstawie pomierzonych różnic wys. i przysp. siły

ciężkości. Dlatego poprawki dyn. Wyk. sa do wyrazania popr. w innych systemach wys.

*g to średnie przyspieszenie na punktach A i B.

*Punkty leżące na tej samej powierzchni ekwipot. maja taka sama wysokosc dyn.

*Wysokości dynam. nie maja żadnej interpretacji geometrycznej.

*Wys. Dyn. nie nadają sie do rozwiązywania zagadnień związanych z wyznaczaniem figury Ziemi wg koncepcji Stokesa.

32. Wys. Ortomet. to odległości punktów fizycznej powierzchni Ziemi od geoidy mierzone wzdłuz linii pionu.

Problem wyznaczenia wartości przeciętnej przyspieszenia - pewne rozw podał Niethammer…Do obliczenia wartości przeciętnych przyspieszenia Niethammer zaproponował wykorzystanie redukcji PoinSarego-Preya obliczona

dla połowy wysokości:
. Jeżeli różnice wysokości zapiszemy w postaci
, to poprawkę ortom. (Niethammera) można zapisać: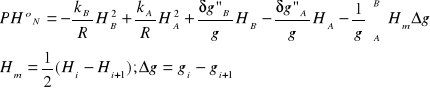

Jest ona rzadko stosowana ze względu na konieczność znajomości rozkładu gęstości i topografii terenu…

33. Przybliżone wys.ortom.

-podejście Helmerta. W terenach płaskich H. zaproponował rezygnacje z poprawek terenowych, co upraszcza wzór na poprawkę ortometryczną do postaci:

Przyjmując ponadto, ze na niewielkim obszarze gęstość skorupy jest taka sama k=ka=KB, a wiec dostaniemy:

Poprawka ta nazywana jest przybliżona poprawka ort. (Helmerta), wysokości przybliz wys.

Ort. Helmerta.

Podsumowanie:

*Wys. ort maja jasna interpretacje geom. Wyrażają one odległości punktu na fizycznej powierzchni Ziemi od

geoidy mierzona wzdłuż linii pionu.

*Punkty leżące na tej samej pow. Ekip. maja zatem rózne wys. Ort.

*Wysokości i poprawki ortometryczne wyznaczane sa z dokładnością zależna od dokładności wyznaczenia przeciętnej wartości przysp. siły ciezosci, która to dokładnosc zalezy głównie od precyzji okreslenia gęstości wierzchnich warstw skorupy ziemskiej i topografii terenu.

*Wys. Ort. dobrze nadają sie do rozwiązywania zagadnień związanych z niwelacja satelitarna (wyznaczaniem geoidy).

34. Pomijając błędy pomiarowe (wspólne dla wszystkich syst wys), na dokładnosc wyznacz. Wys. Ortom. ma wpływ głównie błąd wyznaczenie gęstości powierzchniowych warstw skorupy ziemskiej. Rócnczkujac wzór opisujacy wysokość ortometryczną mamy:

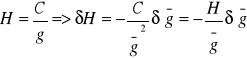
Zaniedbując znak oraz przyjmując g=1000 Gal możemy zapisać:

Co oznacza, ze dla H=1km błąd wyznaczenia wysokości w [mm] wynosi tyle ile błąd wyznaczenia wart przeciętnej przyspieszenia w [mGal].

Redukcje P-P można zapisać w postaci:

Różniczkując względem gęstości dostaniemy:

Z ostatniej zależności wynika:

Dla H=1km =>

35. Popr.ort za pomocą popr.dynam.

36.Wzajemne relacje pomiędzy systemami wysokości:

Wykorzystując zależność.

można otrzymać można szereg równań wiążących różne systemy między sobą.

Np. między wysokością normalną i geopotencjalną istnieje zależność

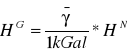
związując zaś wysokość ortometryczną z normalną

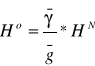
i wreszcie dla wysokości dynamicznej i normalnej

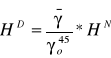
Wysokość normalna określa wzniesienie punktu ponad quasigeoidę mierzone po normalnej linii pionu

1.Zagadnienia brzegowe teorii potencjału:

*nie sa znane bezpośrednie zależności

*poszukiwanie wartości stałych całkowania lub wartości granicznych w teorii równań różniczkowych

*w geod. fizycznej do wyznaczania zagadnień brzegowych stosowana jest metoda rozdzielania zmiennych.

III zagadnienie brzegowe-gdy na gładkiej powierzchni S znana jest kombinacja liniowa potencjalu V i jego pochodnej w kierunku normalnej zewnętrznej do powierzchni S w postaci hV+k(dv/dh) (k i h pewne stale).

III zagadnienie brz.ma szczególne zastosowanie w geod.fizycznej bowiem stanowi model wyznaczenia geoidy z anomalii grawimetrycznych. Dlatego 3 zag.teor.brzegowej nazywamy Zagadnieniem brzegowym geod.fizycznej.

2.Potencjal pływowy-potencjal związany ze zjawiskami pływowymi czyli powodowanymi zmiennym przyciąganiem Księżyca i Słońca.

Potencjał deformacyjny-nasza planeta jest ciałem elastycznym wiec jej reakcja na działanie sil pływowych charakteryzuje się cechami właściwymi ciałom elastycznym. Wynikiem sil pływowych sa pływowe deformacje skorupy ziemskiej (zwane pływami skorupy ziemskiej) oraz przypływy i odpływy mórz i oceanów). Naprężenia pływowe powodują zmiany kształtu Ziemi, te zmiany można traktować jako zmiany przestrzennego rozkładu mas Ziemi. A te zmiany powoduje zmianę potencjału grawitacyjnego Ziemi. Właśnie zmiane potencjału graw. Nazywamy potencjałem deformacyjnym.

Rys. Czarnecki s.140

3.(z zad 2). Liczby Lov'a(wskaźniki związane z elastyczna reakcja Ziemi na naprężenia pływowe)

*1sza liczba Love'a- stosunek rzeczywistego przemieszczenia radialnego elementu masy „Ziemi rzeczywistej” do podobnego przemieszczenia odpowiedniego elementu masy pewnego modelu „Ziemi plynnej”

h-1sza liczba Love'a, h=0 dla Ziemi sztywnej, h=1 dla Ziemi plynnej, 0<h<1 - dla Ziemi rzeczywistej.

*2ga liczba lova => k=(Vd/Vp)(pot.deform/pot.plywowy)

*Liczba Shidy (l)-stosunek elastycznego poziomego przemieszczenia elementu masy Ziemi rzeczywistej do analogicznego przemieszczenia masy hipotetycznej Ziemi płynnej, przy założeniu jednorodności modelu Ziemi a także izotropii warstw poziomych. Liczba Shidy zmienia się tylko wraz z głębokością. Można ja także wiązać z rzędem harmonicznych sferycznych i dla n=2, l=0,08.

4.harmoniczne sferyczne:

Równanie Laplace'a we wspl. Prost. Ma postac:

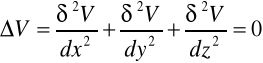
Funkcje spełniające te równanie to f.harmoniczne. Po przekształceniu:

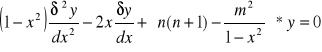
*harmoniczne strefowe: zależne tylko od Ф lub szerokości ρ.

M=0, n=3, n-m=3. Gdy m=0 miejsca zerowe funkcji będą znajdować się na „n” równoleżniku

*H.sektorowe-gdy m=n miejsca funkcji będą znajdować się na 2m południkach. Funkcje zależne tylko od długości lambda.

*harmoniczne tesseralne-gdy m nie równe n - miejsca zerowe będą znajdować się na m-n równoleżnikach i 2m południkach. Te funkcje zależne od szerokości fi i długości lambda.

6.Elip.obrotowa jako modelowa pow.ekwip. potencialu sily ciężkości-

Główne zalodzenia:

*Rozmiary elipsoidy (a,f) - dobranetak aby powierzchnia elipsoidy możliwie najlepiej aproksymowala geoide globalna.

*masa elipsoidy M rowna masie Ziemi,

*Prędkość wirowania elipsoidy w ->równa prędkości kątowej Ziemi

*Powierzchnia elipsoidy jest powierzchnia ekwipotencjalna potencjału siły ciężkości (z def). Uo=Wo=const.

Została zaproponowana przez Somigliane w 1930r ( ta sama powierzchnia odniesienia dla pomiarów geodezyjnych grawimetrycznych)

16.Potencjal zakłócający T(rp)-jest to różnica potencjału rzeczywistego siły ciężkości W(rp) i potencjału normalnego U(rp)

T(rp)=W(rp)-U(rp). Potencjał zakłócający w punkcie P, podobnie jak potencjały rzeczywisty i normalny, jest funkcja położenia punktu w przestrzeni (wektora rp). Zarówno po. rzeczywisty jak i normalny zawierają ten sam „po.odsrodkowy”, w związku z tym z ich różnicy zostaje on wyeliminowany. A Zatem potencjał zakloajacu T jest potencjałem grawitacyjnym i w przestrzeni zewnętrznej jest on funkcja harmoniczna, bowiem spełnią równanie Laplace'a->∆T(rp)=0

17. Anomalia grawimetryczna- różnica modułów wektorów przyspieszenia go=abs(go) na geoidzie i normalnego ye=abs(ye) na elipsoidzie. ∆g=go-ye

Zakłócenie grawimetryczne-pochodna potencjału zakłócającego w kierunku normalnej d powierzchni ekwipotencjalnej W=const.

Różnica dg przyśpieszeń rzeczywistego i normalnego, obu wziętych w tym samym punkcie, na geoidzie.

Odchylenie pionu w 1 wert i południku (rys. Czarnecki stron 180)

18. Podstawowe równanie geodezji fizycznej:

.Równanie to wiąże anomalie grawimetryczne z zakłóceniami grawimetrycznymi oraz z wysokościami geoidy względem elipsoidy. !szy wyraz - wyraz Brunsa, 2gi wyraz-wyraz rzędu spłaszczenia elipsoidy.

Przybliżenie sferyczne tego równania-polega ono na zastąpieniu powierzchni elipsoidy ekwipotencjalnej powierzchnia kuli o takiej samej objętości. Porównując wzory wyrażające objętości elipsoidy i kuli mamy:

Zaniedbując wyrazy rzedu spłaszczenia elipsoidy otrzymamy:

Uwzględniając to kownianie z przybliżeniem sferycznym przyjmie postac:

19.Wzor Stokesa:

, S(Y)-funkcja Stokesa. Trzeba dobrać układ współ. Aby był dogodny do całkowania anomalii graw. Odległość elementu powierzchni sfery jednostkowej dσ od punktu P, w którym wyznaczamy wysokość geoidy N, będziemy Mierzyc wielkością kata odległości sferycznej ψ<0,pi>. Kierunek luku ψ względem południka punktu P określimy za pomoca azymutu alfa<0,2pi>. Element powierzchni sfery jednostkowej w nowym układzie wyrazi się jako: dσ=sin ψd ψdα. Wzór stokesa przyjmie teraz następująca postać:

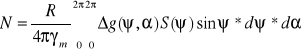
Analizując rysunek: (taki tam rysuneczek z Czarneckiego s.187)

Mamy ze funkcja S(ψ) w punkcie { osiąga wartość nieksończoną. Uniemożliwia to praktyczne stosowanie wzoru Stokesa. Pozbędziemy się wymienionej wady tej funkcji zastępując ja inna funkcja. F(ψ)=0,5*S(ψ)sin ψ, wzór Stokesa będzie wiec:

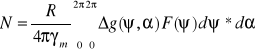
20. Wyznaczanie grawimetrycznych odchyleń pionu. Stokes a Vening-Meinesz.W koncepcji V-M została wykorzystana prosta zależność geometryczna pomiędzy różnica wysokości geoidy wyrażona wzorem Stokesa a nachyleniem geoidy względem elipsoidy geopotencjalnej.
Rys.: Czarnecki s.189

Odchylenie pionu 0 jest to kat pomiędzy normalna do geoidy a odpowiednia normalna do elipsoidy ekwipotencjalnej

42.Niwelacja satelitarna na małych obszarach-Jeżeli na pewnym obszarze objętym siecią punktów GPS, znajdują się takie punkto GPS, które maja określone wysokości ortometryczne lub jeśli niektóre punkty GPS zostały dowiązane wysokościowo do punktów niwelacyjnych w systemie wysokości ortometrycznych to można wyznaczyć przybliżony przebieg geoidy a tym obszarze: 1.nalezy obliczyć odstępy geoidy od elipsoidy (N=Hgeom-Hort). Musi to być na obszarze nizinnym o jednolitej budowie geologicznej i gdy punkty o wyznaczonych wysokościach sa rozmieszczone równomiernie na całym obszarze.

---