Temat: Dalmierze elektromagnetyczne - zasada działania i klasyfikacja

A w nim: Klasyfikacja dalmierzy elektromagnetycznych. Zasada działania dalmierzy impulsowych i fazowych.

Klasyfikacja dalmierzy może być dokonywana przy założeniu rozmaitych kryteriów. Zazwyczaj przyjmuje się dwa:

• ze względu na rodzaj fali (jej długości) przenoszącej sygnały pomiarowe
  Dzielimy je na:

a) elektromagnetyczne
b) ultradźwiękowe

• ze względu na formę sygnałów pomiarowych, która warunkuje sposób pomiaru czasu i rozchodzenia się mierzonej odległości tam i z powrotem. Dzielimy je na:

a) impulsowe, których fala pomiarowa jest w formie pojedynczych impulsów
b) fazowe, których sygnał pomiarowy jest ciągłą falą harmoniczną.

Coraz częściej stosuje się dalmierze, które łączą cechy dalmierzy impulsowych i fazowych. Dzieje się tak dlatego, gdyż dalmierze impulsowe pozwalają na bezlustrowy pomiar a fazowe są dokładniejsze. Dalmierzem fazowym nie można pomierzyć odległości przy stosowaniu jednej częstotliwości fali.

Zasada działania dalmierzy:

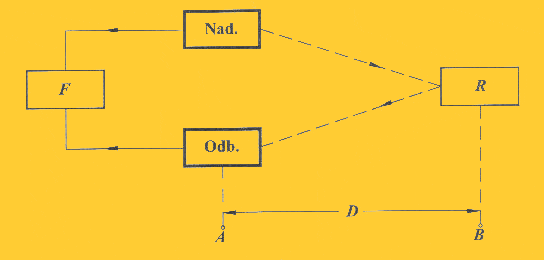
Pomiar odległości D sprowadza się do pomiaru czasu
, w ciągu którego sygnał pomiarowy emitowany z punktu A przebywa drogę 2D równą 2AB

Można, zatem napisać:

Rys.1 Prosty schemat zasady działania dalmierza geodezyjnego

Zasada działania dalmierza impulsowego:

W dalmierzach impulsowych mierzony jest czas od momentu wyjścia konkretnego impulsu do jego powrotu. Czas ten jest mierzony bezpośrednio w precyzyjnych zegarach znajdujących się w dalmierzu.

Po przyjęciu, że prędkość fali elektromagnetycznej jest równa v=300000 km/s i założeniu błędu pomiaru długości 1 mm, otrzymamy, że zegar dalmierza powinien mierzyć czas z częstotliwością:

Schemat blokowy działania dalmierza impulsowego

Rys.2 Schemat blokowy działania dalmierza impulsowego

Dalmierze fazowe

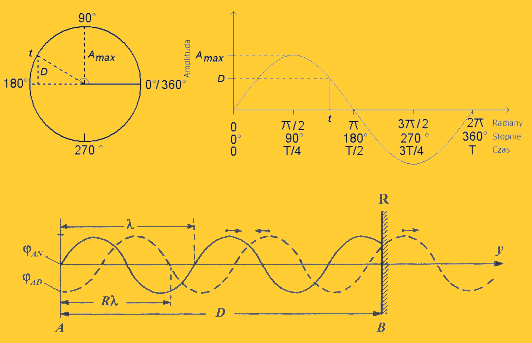
Rys.3 Rozchodzenie się sygnału w przypadku dalmierza fazowego

Równanie fali sinusoidalnej wygląda następująco:

Fala emitowan i odbita różnią się przesunięciem fazowym
związanym z czasem t-


- czas przejścia fali tam i z powrotem

Znając odległość D to możemy wyznaczyć:

gdzie:
o-fala wyjściowa (u nas
o=0)

Przy założeniu, że:

Zatem różnice faz można zapisać jako:

Po przekształceniu otrymujemy:

Mierzona odległość D jest funkcją prędkości rozchodzenia się fali, różnicy faz i częstości kołowej

- odległość D można określić mając długość wzorcową fali

W dalmierzach fazowych nie możemy obliczyć całkowitej ilości odłożeń fali wzorcowej. Jest to problem dalmierzy fazowych, który rozwiązuje się poprzez pomiar na różnych częstotliwościach wzorcowych.

Ostatecznie otrzymujemy:

A wzór na różnice faz sygnału wyjściowego i odebranego wygląda następująco:

Schemat działania dalmierza fazowego

Rys.4 Schemat blokowy działania dalmierza fazowego

Temat: Dokładność pomiaru odległości dalmierzami elektrooptycznymi. Wpływ warunków meteorologicznych

A w nim: Analiza dokładności pomiaru odległości dalmierzami impulsowymi i fazowymi. Ocena wpływu warunków meteorologicznych na otrzymane wyniki.

Dalmierze impulsowe

Po zróżniczkowaniu wzoru na obliczenie odległości dalmierzem impulsowym obliczyć możemy dokładność takiego pomiaru:

gdzie:c - prędkość rozchodzenia się światła w próżni
n - współczynnik załamania ośrodka

- czas mierzony od wyjścia do powrotu impulsu

Składnik
można pominąć, bo wyznaczany jest z błędem:

gdzie, za prędkość fali elektromagnetycznej przyjmujemy:

Z tego wynika, że na dokładność pomiaru dalmierzem impulsowym wpływa dokładność określenia współczynnika załamania n oraz dokładność określenia czasu przebiegu impulsu.

Dalmierze fazowe

Analogiczną analizę można przeprowadzić dla dalmierzy fazowych.
Mierzona odległość przy ich użyciu wyznaczana jest ze wzoru:

gdzie:
-długość fali wzorcowej
Wzór przypomina ten, z którego wyznaczamy długość mierzoną taśmą, czyli jako sumę ilości odłożeń i reszty.

, ponieważ liczba odłożeń jest określana bezbłędnie

Po uproszczeniu dostajemy postać wzoru na błąd standardowy dalmierza:

Współczynnik B zależy od dokładności fazomierza oraz dokładności określenia stałej dalmierza. Wartość współczynnika A jest funkcją stałości częstotliwości wzorcowej.

Wpływ warunków meteorologicznych w dalmierzach

Prędkość rozchodzenia się fali elektromagnetycznej w powietrzu zależy od współczynnika załamania „n” ośrodka, który obejmuje obszar między punktami A i B mierzonej odległości.

Rys.1 Warstwowy model atmosfery wypełniający przestrzeń między punktami A i B

n(x) -nieznana jest postać tej funkcji, dlatego obieramy jej wartość przybliżoną ze wzoru:

 

przy czym ni jest wyliczane dla (ti, pi, ei,
i). Jest to funkcja punktowa, a nie ciągła. Przy odpowiednim zagęszczeniu pomiarów (ti, pi, ei oraz
i) możemy otrzymać wartość porównywalną z n(x).

W praktyce temperaturę, ciśnienie i prężność pary wodnej mierzymy:

• przy bardzo precyzyjnych pomiarach - na początku, w środku i na końcu mierzonego odcinka. Wtedy współczynnik załamania obliczamy ze wzoru:
  

• w średnio dokładnych pomiarach - wyznaczamy średnią z pomiarów (t, p,
  ) na początku i na końcu odcinka.
  
  

• w mniej dokładnych pomiarach - temperaturę mierzymy tylko na stanowisku dalmierza.

W praktyce przy krótszych odległościach stosuje się dalsze uproszczenie, gdzie współczynnik „n” wyznacza się ze średnich wartości pomierzonej temperatury, ciśnienia i prężności pary wodnej

Wzory empiryczne na współczynnik załamania fal elektromagnetycznych w powietrzu:

a) do mikrofal stosuje się wzór Essena-Froome'a:

gdzie:T-temperatura w [K]
p,e - wyrażone w [mm Hg]

Po zróżniczkowaniu powyższego wzoru ze względu na temperaturę, ciśnienie i prężność pary wodnej dla
u>1 otrzymamy:

Wynika z tego, żę:

• Zmiana (błąd pomiaru) temperatury o 1 stopień Celsjusza da nam wartość 1mm/km

• Zmiana (błąd pomiaru) ciśnienia o 1 mm Hg daje błąd pomiaru 0,4 mm/km

• Zmiana (błąd pomiaru) prężności pary wodnej o 1 mm Hg daje błąd pomiaru długości 6,6 mm/km

Stwierdzić można, więc, że decydujący wpływ na błąd pomiaru długości ma wartość wyznaczenia prężności pary wodnej

Wzór Essena-Froome'a jest zalecany przez MUGG do przeprowadzania obliczeń

Wzory na współczynnik załamania dla fal optycznych

Wzór Kohlrauscha:

Gdzie:
-współczynnik rozszerzalności termicznej powietrza. Zwykle przyjmuje się, że wynosi on ?=0,003661
t - temperatura w stopniach Celsjusza
p,e - określone w mm Hg

Wzór Barrella i Sears'a:

-długość fali nośnej (optycznej)

Kolejność obliczeń przy tych dalmierzach jest następująca. Najpierw stosujemy wzór Barella i Sears'a wstawiając do niego długość fali nośnej podawanej przez producenta. Następnie obliczamy ng wstawiając średnie wartości temperatury ciśnienia i prężności pary wodnej oraz obliczamy ng0

Po zróżniczkowaniu podanych wzorów ze względu na występujące zmienne otrzymamy wartości:

Dla fal optycznych zmiana wartości prężności pary wodnej jest wielkością bardzo małą, którą można pominąć.
Ciśnienie zmienia się o 1 mm Hg na 10 metrów wzrostu wysokości, czyli dla wysokości 300 metrów będzie się różnić o 15 mm Hg. Jeżeli tej różnicy nie uwzględnimy to popełnimy błąd 6 mm/km.

Podane wzory w nowoczesnych tachimetrach elektronicznych są „zaszyte” w pamięci procesorów. Po wprowadzeniu pomierzonych (uśrednionych) wartości temperatury i ciśnienia w czasie pomiarów przemnażają one pomierzoną przez dalmierz odległość.

Do pewnej grupy dalmierzy należy wprowadzić do procesora wartości współczynników skali (przeliczeniowych) odczytanych z tabel lub nomogramów na podstawie określonej temperatury i ciśnienia.

Temat: Komparacja dalmierzy elektromagnetycznych

A w nim: Błędy związane z pomiarem długości dalmierzem elektromagnetycznym. Wyznaczenie poprawki stałej dodawania k, poprawki ze względu na zmianę częstotliwości wzorcowej oraz poprawki z tytułu wystąpienia błędu cyklicznego.

Komparacja dalmierzy elektromagnetycznych
Stosując w pomiarach odległości dalmierze elektromagnetyczne musimy uwzględniać wpływy błędów przypadkowych i systematycznych, które obciążają wyniki tych pomiarów. Ogólnie można powiedzieć, że błędy te związane są z samym dalmierzem oraz z wpływem środowiska na sygnał pomiarowy. Te ostatnie zostały omówione na poprzednim wykładzie.

Wyróżnić można następujące błędy instrumentalne:

• Błąd przypadkowy

• Błąd systematyczny niezależny od odległości

• Błąd systematyczny zależny liniowo od odległości

• Błąd systematyczny zależny nieliniowo od odległości

• Błąd cykliczny

• Błąd zależny od temperatury

• Błąd zależny od czasu

• Błąd zależny od napięcia zasilania

Charakterystyka błędów przypadkowych i systematycznych niezwiązanych z instrumentem:

• Błędy centrowania instrumentu i reflektora nad lub pod znakami pomiarowymi

• Błąd poziomowania dalmierza i lustra

• Błąd wycelowania:
  a) dalmierza na lustro
  b) lustra w kierunku dalmierza

• Błąd popełniany przy pomiarach nasadką dalmierczą

• Błąd pomiaru temperatury, ciśnienia i wilgotności na drodze sygnału pomiarowego

• Błąd pomiaru lub zaniechania wprowadzenia którejś z poprawek do długości

• Błędy wynikające z odbicia sygnałów pomiarowych od obiektów będących w tle reflektora

• Błędy wywołane turbulencją atmosferyczną

• Błąd zależny od czasu pomiaru i związany z różną ilością pomiarów przejść fazowych

Celem komparacji jest wyznaczenie błędów systematycznych pochodzenia instrumentalnego, które mogą być wyeliminowane z pomiarów poprzez wprowadzenie do nich poprawek wyznaczonych w procesie komparacji.

W praktyce wyznacza się trzy rodzaje poprawek:
1. Poprawkę stałej dodawania k
2. Poprawkę ze względu na zmianę częstotliwości wzorcowej od jej wartości nominalnej
3. Poprawkę ze względu na błąd cykliczny, która może występować tylko w dalmierzach fazowych

Ad.1 Poprawka stałej dodawania k
Ogólny wzór na obliczenie odległości pomierzonej dalmierzem wygląda następująco:

Stała k łączy ze sobą wpływ różnicy między centrem mechanicznym dalmierza, a jego centrem elektronicznym. Najczęściej wartość stałej k wyznacza się na krótkim odcinku poprzez porównanie odległości pomierzonej i długości wyznaczonej inną metodą, zazwyczaj o rząd dokładniejszą. Odcinek, na którym wykonywane są pomiary powinien mieć około 5-10 metrów. Wartość stałej dodawania obliczamy wówczas ze wzoru:

Pewniejszym sposobem wyznaczenia stałej k jest pomiar odległości 2-3 odcinków o długościach różniących się o 1-2 metry. Najlepiej, jeżeli są to np. odcinki odpowiednio w odległości 10,12 i 15 metrów od instrumentu.

Jeżeli nie znamy długości odcinka z dokładnością o rząd wyższą możemy zastosować inną metodę wyznaczania stałej k. Polega ona na pomiarze długości odcinka AB, na który wtycza się dodatkowo punkt C. Przedstawione to zostało na rysunku obok.

Rys.1 Sposób wykonania bazy pomiarowej

Mierzymy w dwóch kierunkach odcinki AC, CB i AB. Możemy wówczas zapisać prostą zależność łączącą wyniki pomiarów i stałą k dalmierza:

(AC+k)+(CB+k)=AB+k

Z czego po uproszczeniu otrzymujemy wzór na stałą dodawania k:

k=AB-(AC+CB)

Ad.2 Wyznaczenie błędu cyklicznego

Błąd cykliczny wynika z tzw. sprzężeń pasożytniczych występujących między częścią nadawczą a częścią odbiorczą dalmierza. Na sygnał powracający nałożony jest niejako sygnał zakłócający o tej samej częstotliwości. Błąd cykliczny pojawia się także w elektrycznym przesuwniku fazy.
Wartość błędu cyklicznego określamy w następujący sposób. Tworzymy bazę AB, na którą wtyczamy punkt C. Odcinek CB powinien być równy lub trochę dłuższy od połowy długości „przymiaru” podstawowego ? dalmierza. Odcinek ten należy podzielić na dziesięć równych części, których długość równa jest
Pomiary dalmiercze na tej bazie wykonujemy tylko na podstawowej częstotliwości wzorcowej. Obliczamy odchyłki długości pomierzonych od ich nominalnych wartości określonych z o rząd większą dokładnością. Jeżeli odchyłki te dla wszystkich długości są podobne to wartość ta jest stałą dodawania k dalmierza a błąd cykliczny nie występuje. Wówczas, gdy odchyłki są różne rysujemy wykres, na którym przedstawiamy zmiany. Na poniższym rysunku znajduje się przykład takiego wykresu. Służy on do określania poprawek długości dla różnych długości z tytułu błędu cyklicznego.

Rys.3 Wykres będący wynikiem wyznaczenia poprawek z tytułu błędu cyklicznego

 

  Ad.3 Błąd zmiany częstotliwości

Pod wpływem różnych czynników, głównie jednak na skutek starzenia się kwarcu, częstotliwość wzorcowa dalmierza ulega zmianie. Powoduje to zmianę skali mierzonych nim długości. Możemy to zapisać następująco:

gdzie:
-zmiana częstotliwości wzorcowej

-częstotliwość wzorcowa nominalna(znana jest z metryki)

-częstotliwość wzorcowa w czasie pomiaru

W procesie komparacji chodzi zatem o wyznaczenie wartości df. Wykonuje się to poprzez porównanie aktualnej częstotliwości wzorcowej dalmierza fwp z częstotliwością wytwarzaną przez odpowiedni generator. Tego rodzaju bezpośredni pomiar wykonuje się w laboratoriach odpowiednich instytucji. Komparację częstotliwości można realizować także w warunkach polowych przez porównanie aktualnej jej wartości z tzw. krajowym wzorcem częstotliwości fal radiowych emitowanych regularnie przez niektóre radiostacje. Poprawkę z tytułu zmian częstotliwości podaje Polskie Radio codziennie o 12:00.

Obowiązujące przepisy nakładają na użytkowników dalmierzy obowiązek ich okresowej kontroli. W jej wyniku dalmierz uzyskuje tzw. Metrykę. Do wykonywania kontroli, którą nazywamy komparacją dalmierza zostały upoważnione w Polsce Instytut Geodezji i Kartografii w Warszawie oraz kilka instytucji, które założyły i utrymują tzw. Komparatory polowe. Komparatory polowe są to zbiory punktów zestabilizowanych w terenie w linii prostej w postaci postumentów betonowych., których trzon osadzony jest poniżej poziomu zamarzania gruntu. Długości baz takich komparatorów osiągają wartość 1,5 kilometra, a długości odcinków zawarte w tym zakresie wahają się od kilku do kilkunastu metrów. Odcinki komparatorów są wyznaczane i znane z dokładnością o rząd większą niż posiadają badane na nich instrumenty.

Temat: Elektroniczne systemy pomiaru kątów

A w nim: Charakterystyka elektronicznych systemów pomiaru kątów - kodowego, impuslowego i dynamicznego.

Dotychczasowe systemy pomiaru kątów lub kierunków wykorzystywały optyczne urządzenia, które pozycjonowały położenie osi celowej lunety na kręgu poziomym. Wykonanie odczytu w danym systemie optycznym określało kierunek osi celowej względem zera kręgu poziomego. Kąt określony był z różnicy odczytów dwóch kierunków. Dążąc jednak do jak największej automatyzacji pomiarów niezbędne okazało się zastosowanie elektronicznych systemów pomiaru kątów. Pozwoliły one na wykluczenie odczytu kierunku przez obserwatora zwiększając w ten sposób wydajność pomiarów. Dodatkowo umożliwiły one rejestracje oraz automatyczne opracowanie wyników pomiarów. Elektroniczne system pomiaru kierunków wymagają zastosowania przetworników zamieniających mierzony kierunek na odpowiednie sygnały elektroniczne. Sygnały elektroniczne powinny zostać przetworzone w taki sposób, aby uzyskać wielkości dogodne do obliczania, wyświetlania i rejestracji kierunków.

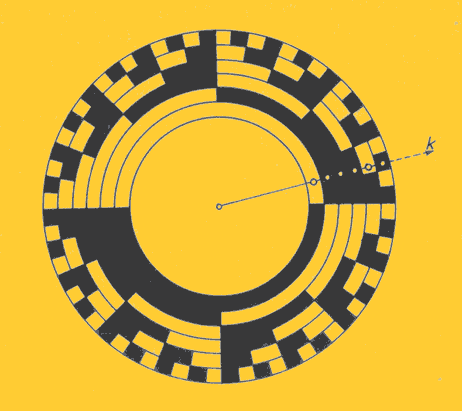
Rys. 1 Tarcza kodowa

W istniejących i stosowanych aktualnie systemach elektronicznych można wyróżnić dwa rodzaje przetworników typu kąt-napięcie (natężenie):
Grupa I - przetworniki położenia, każdemu położeniu lunety teodolitu odpowiada jednoznacznie określony stan napięcia. Należą do tej grupy przetworniki kodowe.
Grupa II - przetworniki kąta, odpowiednim zmianom położenia lunety odpowiada ściśle określona liczba impulsów - przetworniki impulsowe.

Systemy kodowe pomiaru kierunków
W jednoznaczny sposób wyświetlają położenie osi lunety do położenia zerowego(system bezwzględny). Najistotniejszym elementem systemu jest tarcza kodowa zastępująca krąg poziomy w teodolicie(patrz rys.1). Sprężona jest z alidadą teodolitu, na której jest luneta. Na tarczy kodowej znajduje się wiele koncentrycznych ścieżek o różnych średnicach, przy czym na każdej z tych ścieżek znajduje się na przemian ległe pola jasne i ciemne. Uzyskanie odpowiedniej dokładności odczytu kierunku wymaga zastosowania tarczy kodowej z odpowiednią liczbą ścieżek, z których ostatnia musi być podzielona na pola o bardzo małych odstępach. Na przykład chcąc uzyskać dokładność 1cc ilość ścieżek musiałaby wynosić 222. Przy średnicy koła 13 cm szerokość ścieżki musiałaby być równa 0,097µm. Wykonanie tak drobnego podziału jest niemożliwe. W praktyce uzyskano najwyżej 12 ścieżek, co daje dokładność 10c pomiaru kierunku. Istnieje, więc bariera technologiczna, która powoduje, że ten system jest stosowany w wielu teodolitach najwyżej do pomiaru zgrubnego.

Zasada działania
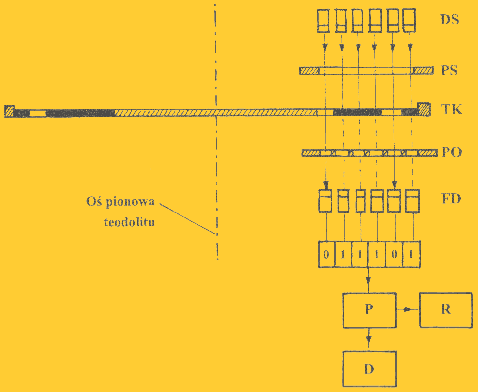
W nieruchomej części teodolitu znajduje się czytnik w postaci matrycy fotoelektrod i fotodiód, które oświetlają fotodetektory równoległą wiązką optyczną (rys.2).

Rys. 2 Zasada funkcjonowania czytnika fotodiodowego

Wiązka przepuszczana przez pola przeźroczyste kręgu wzbudza w odpowiedniej diodzie sygnał elektryczny (napięcie). Sygnał nie powstanie, gdy na drodze wiązki znajdzie się pole nieprzeźroczyste. W każdym fotodetektorze powstać mogą, więc dwa stany kodu dwójkowego. Gdy połączymy wszystkie odczyty z matrycy fotodetektorów otrzymamy odczyt kierunku w kodzie dwójkowym.

Systemy impulsowe pomiaru kierunków
W odróżnieniu od systemu kodowego zastosowano w nim tarcze z jedną ścieżką zawierającą N równych interwałów oraz czytnik impulsów, generowanych w trakcie obrotu tarczy. Tarcza i czytnik tworzą tzw. impulsowy przetwornik kąta. Przetwornik taki może działać na zasadzie galwanicznej, magnetycznej lub optycznej. W przyrządach geodezyjnych stosowane są tylko przetworniki optyczne ze względu na swoją najwyższą dokładność.
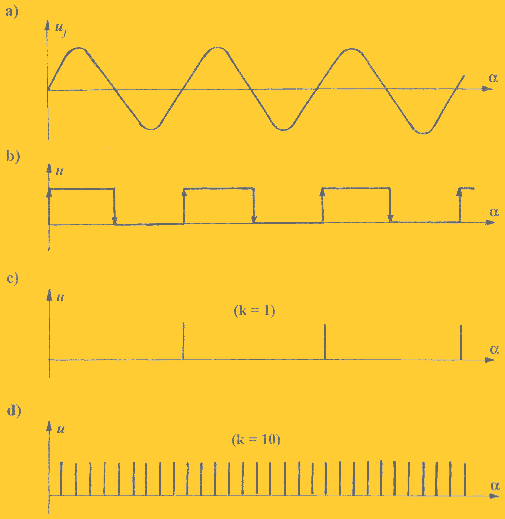
W przetworniku ścieżka kręgu podziałowego zawiera N pól przeźroczystych oddzielonych od siebie polami nieprzeźroczystymi. Przy czym podstawową działką systemu jest tak zwany inkrement o szerokości 2N (pole przeźroczyste i nieprzeźroczyste). Wartość kątowa takiego inkrementu równa się 400g/N. Sygnał elektryczny, który powstaje w fotodiodzie, jest najpierw wzmacniany a następnie przekształcany w przebieg prostokątny. Ten po zróżniczkowaniu zamieniany jest na przebieg impulsowy (Rys. 3).

Rys. 3 Przebieg obróbki sygnału elektrycznego z fotodiody

Ilość impulsów zliczana jest przez licznik. Na jej podstawie wyznacza się wartość kąta na podstawie zależności:
.
Współczesne teodolity elektroniczne zawierają do 100 rysek na 1 milimetr obwodu tarczy, co daje ok. 20 000 rysek na średnicy tarczy ok. 636 mm. Jedno pole pomiarowe jest równe 2c Dokładność takiego pomiaru zwiększa pomiar reszty d. Tą resztę dopełniającą wartość zgrubną kąta wyznacza się drogą interpolacji np. w jednym z rozwiązań może być zagęszczanie impulsów szpilkowych impulsami o większej rozdzielczości. Wtedy stosując n-krotne jej zwiększanie kąt wyznaczamy ze wzoru:

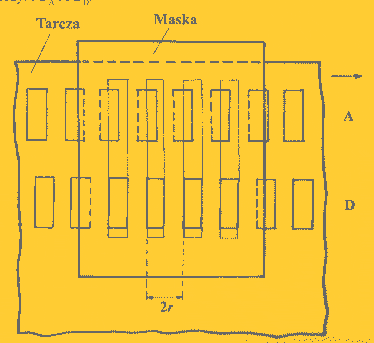
Opisany powyżej sposób pomiaru nie pozwala na określenie kierunku ruchu tarczy. Gdy zmienilibyśmy ten kierunek na przeciwny impulsy zliczane były by w dalszym ciągu powiększając wynik, co nie byłoby zgodne z prawdą. Dlatego przy impulsowym pomiarze kierunków niezbędne jest zastosowanie rozwiązania konstrukcyjnego pozwalającego na wykrycie kierunku ruchu oraz uwzględnienie go w wynikach. Przykładem może być zastosowanie tarczy z dwoma identycznymi ścieżkami rysek impulsowych - zasadniczej A i pomocniczej D (Rys.4).

Rys. 4 Schemat zastosowania tarczy z dwoma identycznymi ścieżkami rysek impulsowych

Interwały ścieżki pomocniczej D przesunięte są względem A o 1 ich długości 2r. Dzięki temu po przekształceniach sygnałów z obu ścieżek uzyskuje się różny przebieg dla różnych kierunków ruchu alidady. Zastosowanie tego rozwiązania pozwala dodatkowo na czterokrotne zwiększenie rozdzielczości.

Dynamiczny system pomiaru kątów
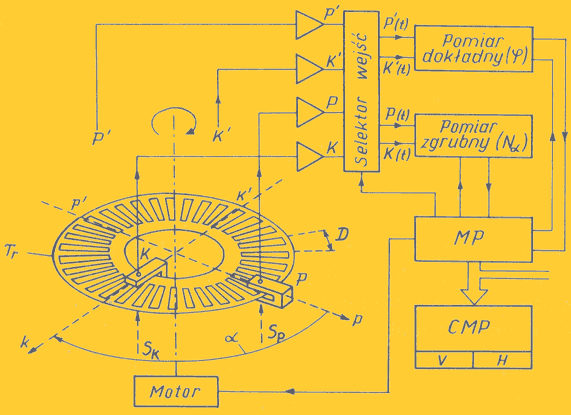
System ten jest systemem impulsowym, składającym się z wirującej tarczy z naniesionymi polami przeźroczystymi i nieprzeźroczystymi oraz dwóch czytników fotoelektrycznych określających bezwzględne położenie obydwu ramion mierzonego kąta (Rys.5).
Pomiar kąta składa się z pomiaru zgrubnego i dokładnego. Do pomiaru zgrubnego na tarczy umieszczony jest dodatkowy element, który uruchamia system w momencie przejścia przez pierwszy czytnik i zamyka przy przejściu przez drugi. Zliczane są przy tym całkowite ilości interwałów pomiarowych. Pomiar precyzyjny jest w zasadzie pomiarem różnicy czasów między sinusoidalnymi sygnałami pomiarowymi powstającymi w obu czytnikach - jednym nieruchomym związanym ze spodarką i drugim ruchomym związanym z lunetą. Różnica czasów określona jest pośrednio jako różnica kątów fazowych jak w fazomierzach cyfrowych dalmierzy elektronicznych. Dzięki temu, że różnica faz jest uśredniana z kilku tysięcy okresów to dokładność tego systemu jest w zasadzie większa od klasycznych systemów impulsowych.

Rys. 4 Schemat zastosowania tarczy z dwoma identycznymi ścieżkami rysek impulsowych

Nie trzeba przy tym stosować zwiększonej rozdzielczości przez zwiększenie częstotliwości zliczania impulsów. Jest to układ prosty. W systemie tym określone jest położenie kierunkowe osi celowej względem czytnika nieruchomego, które odpowiada jak gdyby położeniu kręgu poziomego w optycznych teodolitach.

Cechy światła laserowego

Z samego zjawiska emisji wymuszonej wynikają następujące, podstawowe cechy światła laserowego:

1.Monochromatyczność - ciąg falowy ma tę samą długość fali

2.Równoległość promieniowania

3.Uporządkowanie czasowo-przestrzenne emitowanej fali, które nazywamy koherencją lub spójnością
Rozróżniamy spójność przestrzenną i czasową. Światło spójne jest skłonne do interferencji tzn. ,że dwa ciągi falowe wyodrębnione z wiązki takiego światła interferują ze sobą. Jeśli interferują dwa ciągi falowe emitowane z różnych punktów lasera to mówimy o spójności przestrzennej. Jeśli interferują ciągi falowe emitowane z tego samego punktu lasera ale w różnym czasie, to mówimy o spójności czasowej. Eksperyment, którym możemy sprawdzić czy laser emituje promieniowanie spójne (spójność przestrzenna) jest doświadczenie z oświetleniem wiązką laserową dwóch szczelin.

Rys.5 Interferometr Michelsona

Natężenie światła w punkcie P:

gdzie:
I - natężenie w punkcie P pochodzące od wiązki 1 i 2
Ip - natężenie całkowite w punkcie P

- współczynnik koherencji prążków interferencyjnych

- różnica faz między promieniami r 1 i r 2

Spójność czasową można wykazać poprzez przeprowadzenie eksperymentu z interferometrem Michelsona.

Rys.6 Interferometr Michelsona

Klasyfikacja funkcji i zastosowania laserów w geodezji

Funkcje

1.Wizualizacja w przestrzeni linii, płaszczyzn i punktów pomiarowych

a) poziomych

• niwelatory laserowe

• niwelatory optyczne z laserami lub nasadkami laserowymi

b) pionowych

• pionowniki laserowe

• pionowniki optyczne z laserami

c) dowolnie nachylone

• teodolity laserowe

• teodolity optyczne z laserami

• rzutniki, projektory laserowe

• aliniometry laserowe

• inne

2. Źródła fali nośnej i pomiarowej w dalmierzach optoelektrycznych

• elektrooptyczne dalmierze laserowe

• interferometry laserowe

3.Sterowanie położeniem, kierunkiem i pracą maszyn

8

---