1998/99	LABORATORIUM Z FIZYKI
Ćwiczenie nr 63	PROCESY FIZYCZNE W LAMPACH ELEKTRONOWYCH
ELEKTRONIKA gr. 1.2	Paweł Wojdaszko
Data wykonania:			Ocena	Podpis
1999.05.16	TT
	S

Zasada pomiaru:

Celem ćwiczenia jest zbadanie zależności natężenia prądu emisji termoelektrycznej od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu metodą prostych Richardsona.

Gęstość prądu nasycenia jn - wielkość wyrażająca prąd termoelektryczny z jednostki powierzchni katody - wzrasta ze wzrostem jej temperatury. Wartość jn wyraża wzór Richardsona - Duchmana:

jn - gęstość prądu nasycenia; T - temperatura; Ww - praca wyjścia; k - stała Boltzmana

W interesujących nas zakresach temperatur, decydujący wpływ na wartość prądu nasycenia ma wykładnik potęgowy. Logarytmując wzór zamieszczony wyżej otrzymujemy:

Wykresem tej zależności w układzie współrzędnych (lnjn, 1/T) jest prosta Richardsona:

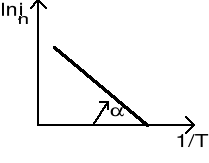
Wyrażenie
jest współczynnikiem kierunkowym prostej. Z wykresu i w oparciu o wzór na ln j_n można więc wyznaczyć pracę wyjścia Ww:

Ww = k tg

Temperaturę katody można wyznaczyć w oparciu o prawo Stefana - Boltzmana. Moc wypromieniowywana przez jednostkę powierzchni katody o temperaturze T (i jednocześnie moc żarzenia na jednostkę powierzchni katody - zużywana przez katodę na promieniowanie) wynosi:

= 5,67*10-12 W/cm2K4

ε = 0,5 (emisyjność całkowita lampy)

Stąd temperatura wynosi:

Układ pomiarowy: (1) I_N; (2) U_Ż; (3) I_Ż

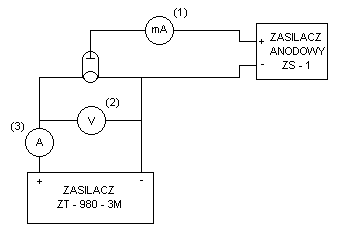
Ocena dokładności pojedynczych pomiarów:

amperomierz (Iż) - miernik uniwersalny METEX:

- zakres: 2 A

- sposób obliczania błędów pomiarowych:

0,8% wartości wskazywanej + wartość ostatniej cyfry

miliamperomierz (In):

- klasa dokładności: 0,5

- zakresy: 7,5 mA; 30 mA

woltomierz (Uż):

- klasa dokładności: 0,5

- zakres: 3,0

Tabele wyników:

1. tabela pomiarowa:

Lp.	Ua = 150 [V]
		IŻ + ΔIŻ	UŻ + ΔUŻ	IN + ΔIN
		[A]	[V]	[mA]
1.	0,54 ± 0,01	1,20 ± 0,04	0,15 ± 0,04
2.	0,56 ± 0,01	1,30 ± 0,04	0,35 ± 0,04
3.	0,58 ± 0,01	1,35 ± 0,04	0,70 ± 0,04
4.	0,60 ± 0,01	1,45 ± 0,04	1,20 ± 0,04
5.	0,62 ± 0,01	1,55 ± 0,04	2,20 ± 0,04
6.	0,64 ± 0,01	1,65 ± 0,04	3,60 ± 0,04
7.	0,66 ±0,01	1,70 ± 0,04	5,40 ± 0,04
8.	0,68 ± 0,01	1,85 ± 0,04	8,50 ± 0,08
9.	0,70 ± 0,01	1,95 ± 0,04	11,75 ± 0,08
10.	0,72 ± 0,01	2,05 ± 0,04	18,50 ± 0,15
11.	0,74 ± 0,01	2,15 ± 0,04	26,50 ± 0,15

b) tabela wyników obliczeń:

Lp.	PŻ ± ΔPŻ	T	T^-1 ± ΔT^-1	jN	ln jN
		[W]	[K]	[K^-1]*0.001		[mA/cm^2]
1.	0,59 ± 0,034	692	1,48 ± 0,10	0,05	- 2,98
2.	0,67 ± 0,041	612	1,43 ± 0,10	0,30	- 1,23
3.	0,75 ± 0,037	725	1,39 ± 0,10	0,60	- 0,52
4.	0,84 ± 0,039	745	1,36 ± 0,10	1,10	0,09
5.	0,92 ± 0,041	764	1,32 ± 0,10	1,95	0,66
6.	1,02 ± 0,043	782	1,29 ± 0,11	3,41	1,22
7.	1,10 ± 0,044	794	1,27 ± 0,11	5,50	1,70
8.	1,20 ± 0,046	817	1,24 ± 0,11	9,60	2,26
9.	1,30 ± 0,048	833	1,21 ± 0,11	14,60	2,68
10.	1,40 ± 0,050	850	1,19 ± 0,11	21,00	3,04

Wartość tgα została wyznaczona na podstawie regresji liniowej za pomoca programu Exel

Wykres zaleznosci Lnjn=f(1/T) przyjal rownanie: y= -19,512x + 26,435

Tangens kata nachylania wykresu do osi ukladu wynosi : tgα=0,98 K

Za pomoca wzoru W_w = k*tgα

Gdzie:

k-stala Boltzmana (k=1,38 * 10^-23 J/K)

stad : W_w = 1,38 * 10^-23 J/K * 0,98 K = 1,26 * 10^-23 eV

wiedzac ze 1 eV=6,24 * 10^-18 eV stad W_w =1,94356 eV = 1,94 eV

W_w = 1,94 eV

Przykładowe obliczenia: (pomiar 6)

Iż = 0,64 A

Iż= [(0,8%*0,64)+0,001] A = 0,006 A 0,01 A

Iż = (0,64 0,01) A

Uż : (zakres: 7,5 V)

Uż = 1,65 V

Uż: (klasa przyrządu: 0,5)

Uż= [(0,5*7,5)/100] V = 0,0375 V 0,04 V

Uż = (1,65 0,04 ) V

In: (zakres: 7,5 mA)

In = 3,60 mA

In: (klasa przyrządu: 0,5)

In= [(0,5*7,5)/100] mA = 0,038 mA 0,04 mA

In = (3,60 0,04 ) mA

Sk=1 cm2

Pz= 1,65*0,64/1 = 1,056 W

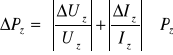
= (0,04/1,65+0,01/0,64) * 1,056 = 0,0421 0,043

Pż= (1,056 0,043) W

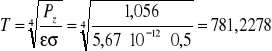
T=281 K

1/T = 0,001278 /K → 0,002 /K

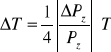
=[(0,25*0,041)*782] K = 8,0155; /T → 0,12575 → 0,126 /K

1/T = (0,002 0,12) /K

= (3,60/1) mA/cm2 = 3,60 mA/cm2

lnjn= 1,28093 → 1,281

lnjn=(In/In)*lnjn= 0,04/3,60 * 1,28 = 0,015 mA/cm2

lnjn=(1,28 0,015) mA/cm2

Dyskusja błędów:

Błędy zastosowanych przyrządów pomiarowych podane są w punkcie o dokładności pojedyńczych pomiarów oraz w punkcie, gdzie pokazane były przykładowe obliczenia. Błędy wielkości złożonych zostały obliczone metodą różniczki logarytmicznej, gdyż wszystkie one są wielkościami iloczynowymi:

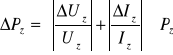
( i - stałe)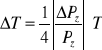

(Sk - stała)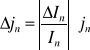

Zestawienie wyników pomiarów:

Wszystkie wyniki pomiarów jak i obliczeń zawiera punkt tabele pomiarowe.

Wnioski i uwagi:

Przeprowadzane doświadczenie miało na celu wyznaczenie pracy wyjścia elektronów metodą prostych Richardsona dla wolframu.

Wynik jest porównywalny z wartościami pracy wyjścia różnych metali, podawanymi w tabelach - od 1,8 eV dla litu do 4,7 eV dla srebra. Wartość średnia pracy wyjścia elektronu z katody badanej lampy, obliczona na podstawie dołączonego do sprawozdania wykresu, wyniosła ok. 1,3 eV. Przy czym niedokładność (błąd) pomiaru tej wielkości wahała się w granicach ±0,24.

Praca wyjścia elektronu z katody badanej lampy wynosi:

Ww = 1,94 eV

Na niedokładność pomiarów wpływ mogła mieć niestabilna wartość wielkości mierzonych wynikająca z dużej czułości elementu użytego w doświadczeniu.

Na wartość błędu wielkości mierzonych wpływ mógł mieć ewentualny błąd popełniony przez obserwatora. Nawiew chłodnego powietrza (otwarte okno) powodował trudności z ustaleniem się temperatury katody. Konsekwencją tego mógł być błąd w odczytywaniu oraz idące za tym pomiary wpisywane do tabeli. Dodatkowo możliwy był również błąd pomiaru natężenia, mógł on wynikać z lekko wygiętej wskazówki amperomierza.

---