WŁASNOŚCI ROZRWORÓW ROZCIEŃCZONYCH : WIELKOŚCI KOLIGATYWNE
Omówimy teraz własności roztworów rozcieńczonych, które są od siebie na pierwszy rzut oka bardzo odmienne, jednak mają pewien wspólny mianownik. Dlatego tez omawiamy je razem. Własności (wielkości) te noszą wspólną nazwę wielkości koligatywnych.
Wyróżniamy cztery wielkości koligatywne :
Obniżenie prężności pary rozpuszczalnika nad roztworem substancji nielotnej
Podwyższenie temperatury wrzenia roztworu substancji nielotnej w stosunku do czystego rozpuszczalnika
Obniżenie temperatury krzepnięcia roztworu, w którym rozpuszczalnik i substancja rozpuszczona tworzą układ eutektyczny, w stosunku do czystego rozpuszczalnika
Ciśnienie osmotyczne
Zanim przejdziemy do omówienia tych wielkości, przypomnijmy, w jaki sposób można wyrazić stężenie substancji rozpuszczonej.
Ułamek molowy 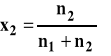
Ułamek wagowy (zwykle wyrażany w procentach) 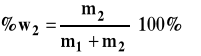
Stężenie wagowe (masowe) 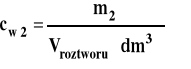
Stężenie molowe 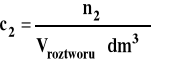
Stężenie molarne 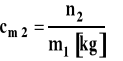
gdzie : n2 - liczba moli substancji rozpuszczonej n1 - liczba moli rozpuszczalnika m2 - masa substancji rozpuszczonej m1 - masa rozpuszczalnika
Sposoby przeliczania tych różnych sposobów wyrażania stężeń na wzajem na siebie powinni Państwo już umieć. Jeśli macie z tym problemy, należy sobie tę wiedzę przypomnieć.
Obniżenie prężności pary rozpuszczalnika nad roztworem substancji nielotnej
Rozpatrujemy roztwór doskonały substancji nielotnej w stałej temperaturze. Substancja nielotna ma praktycznie zerową prężność par w danej temperaturze.
![]()
Prężność par nad roztworem jest równa sumie prężności par obu składników, a ponieważ składnik rozpuszczony ma zerową prężność, to nad roztworem mamy tylko pary rozpuszczalnika.
![]()
Ułamek molowy rozpuszczalnika w roztworze możemy powiązać z ułamkiem molowym substancji rozpuszczonej :
![]()
Wobec tego :
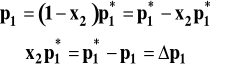
Ostatecznie możemy powiązać obniżenie prężności pary rozpuszczalnika nad roztworem substancji nielotnej z ułamkiem molowym substancji rozpuszczonej.
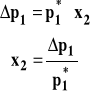
Pomiar prężności pary nad roztworem substancji nielotnej wykorzystywany jest do wyznaczania masy cząsteczkowej substancji rozpuszczonej w tak zwanej metodzie izopiestycznej, której omówienie tu pomijamy, natomiast poznacie ją na ćwiczeniach rachunkowych.
Podwyższenie temperatury wrzenia roztworu substancji nielotnej w stosunku do czystego rozpuszczalnika
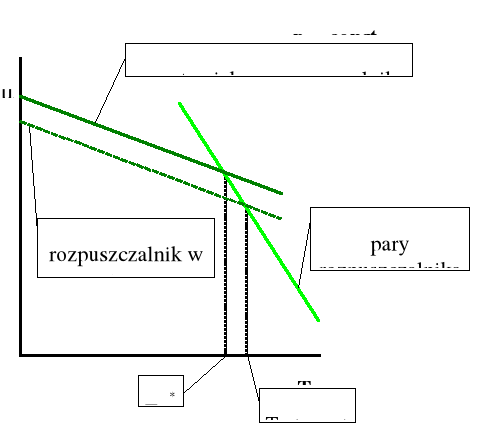
Rozpatrujemy teraz doskonały roztwór substancji nielotnej pod stałym ciśnieniem. Wiemy już, że dodatek nielotnej substancji powoduje obniżenie prężności pary nad roztworem. Jak wiemy, ciecz zaczyna wrzeć, gdy równowagowa prężność par nad nią staje się równa ciśnieniu zewnętrznemu (atmosferycznemu). Na rysunku 1 pokazano zależność prężności pary nad czystym rozpuszczalnikiem i nad roztworem w zależności od temperatury. Ponieważ ułamek molowy rozpuszczalnika w roztworze jest mniejszy od jedności, to krzywa dla roztworu leży pod krzywą dla czystego rozpuszczalnika.
Rysunek 1. Zależność prężności pary od temperatury nad czystym rozpuszczalnikiem i nad roztworem substancji nielotnej.
Na rysunku tym widać jasno, że temperatura wrzenia roztworu substancji nielotnej jest wyższa niż czystego rozpuszczalnika. Na rysunku 2 pokazano zależność potencjału chemicznego rozpuszczalnika w fazie ciekłej i gazowej od temperatury.
Rysunek 2. Zależność potencjału chemicznego rozpuszczalnika od temperatury w fazie ciekłej i gazowej.
Potencjał chemiczny rozpuszczalnika w roztworze można wyrazić jako (przy założeniu doskonałości roztworu) :
![]()
Ponieważ ułamek molowy rozpuszczalnika w roztworze jest mniejszy od jedności, to potencjał chemiczny rozpuszczalnika w roztworze jest zawsze niższy niż czystego rozpuszczalnika
![]()
W stanie równowagi potencjał chemiczny rozpuszczalnika w fazie ciekłe i fazie gazowej musi być taki sam. Ponieważ linia opisująca zależność potencjału chemicznego rozpuszczalnika w roztworze od temperatury leży poniżej linii dla czystego, ciekłego rozpuszczalnika, to jej punkt przecięcia z linią dla rozpuszczalnika w stanie gazowym leży przy wyższej temperaturze. Jeszcze raz widzimy, że roztwór substancji nielotnej ma wyższą temperaturę wrzenia niż czysty rozpuszczalnik pod tym samym ciśnieniem. Warunek równowagi dla roztworu i par rozpuszczalnika wygląda następująco :
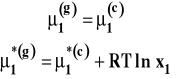
Z tego warunku można wyprowadzić wzór opisujący od czego zależy podwyższenie prężności pary nad roztworem substancji nielotnej (wyprowadzenie pomijamy).
Wzór ebulioskopowy (ebuliometryczny)
![]()
Podwyższenie temperatury wrzenia ![]()
Stała ebulioskopowa 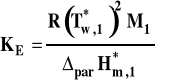
gdzie : cm2 - stężenie molarne substancji rozpuszczonej (w mol/kg) M1 - masa cząsteczkowa rozpuszczalnika parH*m,1 - molowa entalpia parowania rozpuszczalnika
Jednostką stałej ebulioskopowej jest kg·K/mol. Do pomiaru temperatury wrzenia wykorzystywane są urządzenia zwane ebuliometrami np. ebuliometr Świętosławskiego (rysunek 3). Podczas pomiaru temperatury wrzenia istotne jest, aby zaistniała rzeczywista równowaga pomiędzy parą a cieczą. Nie wystarczy włożyć termometr do naczynia z wrzącą cieczą, gdyż rzeczywista temperatura wrzenia jest zawsze nieco wyższa od temperatury równowagowej pod danym ciśnieniem, ze względu na tak zwane przegrzanie cieczy spowodowane koniecznością pokonania przez powstające pęcherzyki pary napięcia powierzchniowego cieczy. W ebuliometrze mierzona jest temperatura równowagi pomiędzy cienką warstwą cieczy na końcówce termometru a parą.
Rysunek 3. Ebuliometr Świętosławskiego.
Pomiar podwyższenia temperatury wrzenia roztworu jest wykorzystywany do wyznaczania masy cząsteczkowej substancji rozpuszczonej. Co w tym celu należy zrobić ? Trzeba zmierzyć temperaturę wrzenia czystego rozpuszczalnika. Następnie trzeba zrobić roztwór substancji, rozpuszczając określoną jej ilość w znanej masie rozpuszczalnika i zmierzyć temperaturę wrzenia tego roztworu. Mając te wyniki, możemy obliczyć masę cząsteczkową substancji rozpuszczonej, przekształcając wzór ebuliometryczny.
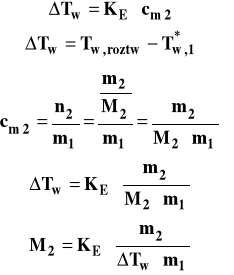
Należy pamiętać, aby masę rozpuszczalnika m1 podstawić wyrażoną w kilogramach. Metody ebuliometrycznej nie można stosować do pomiaru masy cząsteczkowej substancji, która jest lotna czyli ma mierzalną prężność par w warunkach pomiaru.
Obniżenie temperatury krzepnięcia roztworu substancji, która tworzy z rozpuszczalnikiem układ eutektyczny, w stosunku do czystego rozpuszczalnika
W przypadku układu eutektycznego, gdy zaczniemy ochładzać roztwór, zacznie z niego krystalizować czysty rozpuszczalnik. A więc w równowadze w temperaturze krzepnięcia będziemy mieć roztwór nasycony i czysty, stały rozpuszczalnik. Na rysunku 4 pokazano zależność potencjału chemicznego rozpuszczalnika od temperatury w stanie stałym i ciekłym (czystego i w roztworze).
Rysunek 4. Zależność potencjału chemicznego rozpuszczalnika od temperatury w fazie stałej i ciekłej.
Potencjał chemiczny rozpuszczalnika w roztworze jest zawsze niższy niż czystego, ciekłego rozpuszczalnika, gdyż zakładając doskonałe zachowanie roztworu, wyraża się on wzorem :
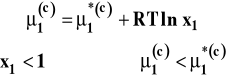
W stanie równowagi potencjał chemiczny rozpuszczalnika w obu fazach jest taki sam. Wobec tego punkty przecięcia krzywych opisujących zależność potencjału chemicznego od temperatury na rysunku 4 pokazują temperatury krzepnięcia czystego rozpuszczalnika i roztworu. Jak widać, temperatura krzepnięcia roztworu jest niższa niż czystego rozpuszczalnika. Z warunku równowagi pomiędzy fazą ciekła a stałą :
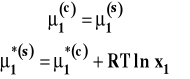
można wyprowadzić wzór opisujący obniżenie temperatury krzepnięcia roztworu względem czystego rozpuszczalnika (wyprowadzenie pomijamy). Należy jeszcze raz podkreślić, ze dotyczy to wyłącznie sytuacji, gdy rozpuszczalnik i substancja rozpuszczona tworzą układ eutektyczny.
Wzór kriometryczny
![]()
Obniżenie temperatury krzepnięcia ![]()
Stała krioskowa 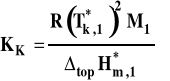
gdzie : cm2 - stężenie molarne substancji rozpuszczonej (w mol/kg) M1 - masa cząsteczkowa rozpuszczalnika topH*m,1 - molowa entalpia parowania rozpuszczalnika
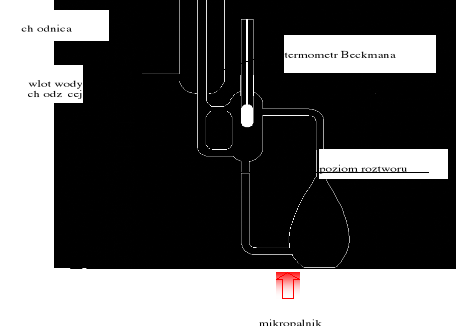
Jednostką stałej krioskopowej jest kg·K/mol. Do pomiaru temperatury topnienia służą urządzenia zwane kriometrami np. kriometr Beckmana (rysunek 5).
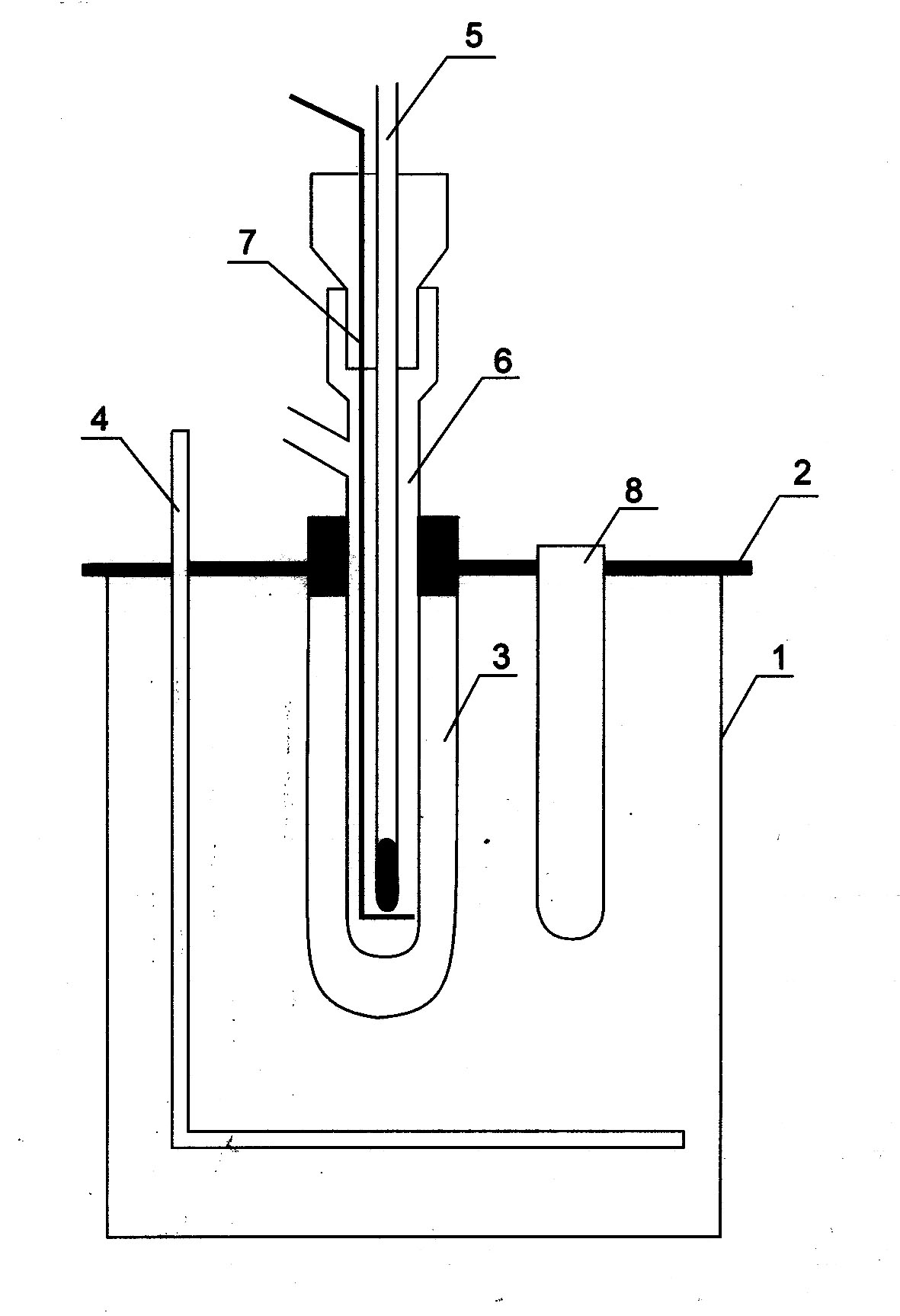
Rysunek 5. Kriometr Beckmana ; 1 - pojemnik z mieszaniną chłodzącą (NaCl + lód;) 2 - pokrywa; 3 - probówka ochronn;a 4 - mieszadło 5 - termometr Beckmana; 6 - naczyńko kriometryczne; 7 - mieszadło; 8 - probówka.
Pomiar obniżenia temperatury krzepnięcia roztworu jest wykorzystywany do wyznaczania masy cząsteczkowej substancji rozpuszczonej. Co w tym celu należy zrobić ? Trzeba zmierzyć temperaturę krzepnięcia czystego rozpuszczalnika. Następnie trzeba zrobić roztwór substancji, rozpuszczając określoną jej ilość w znanej masie rozpuszczalnika i zmierzyć temperaturę krzepnięcia tego roztworu. Mając te wyniki, możemy obliczyć masę cząsteczkową substancji rozpuszczonej, przekształcając wzór kriometryczny.
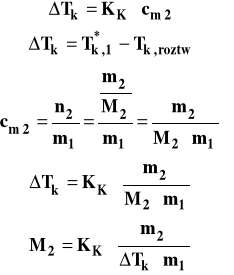
Należy pamiętać, aby masę rozpuszczalnika m1 podstawiać wyrażoną w kilogramach.
Porównanie metod kriometrycznej i ebuliometrycznej wyznaczania masy cząsteczkowej substancji rozpuszczonej
Mamy dwie bardzo podobne metody wyznaczania masy cząsteczkowej substancji rozpuszczonej. W obu trzeba zmierzyć temperaturę wrzenia/krzepnięcia czystego rozpuszczalnika i roztworu o znanym składzie (masowo). Która więc z nich jest lepsza ? Odpowiedź brzmi - zawsze kriometryczna. Przyczyn po temu jest wiele :
Stała krioskopowa dla każdego rozpuszczalnika jest większa niż ebulioskopowa, gdyż entalpia topnienia jest znacznie niższa niż parowania. Toteż dla tego samego roztworu obserwujemy wyraźnie większą różnicę temperatur krzepnięcia pomiędzy roztworem a czystym rozpuszczalnikiem.
Temperatura wrzenia zależy silnie od ciśnienia, a temperatura krzepnięcia praktycznie nie zależy. Wobec tego wyniki uzyskane w wyniku pomiaru temperatury krzepnięcia nie zależą od zmiany ciśnienia atmosferycznego w trakcie pomiarów.
Pomiar temperatury krzepnięcia jest dokładniejszy niż temperatury wrzenia i technicznie prostszy. W przypadku pomiarów temperatury wrzenia nie zawsze mamy z w pełni ustaloną równowagą ciecz - para.
Praca z wrzącymi rozpuszczalnikami organicznymi jest niebezpieczna, a przecież nie zawsze pracujemy z roztworami wodnymi.
Ciśnienie osmotyczne
Rozpatrujemy układ w stałej temperaturze składający się z czystego rozpuszczalnika i roztworu rozdzielonych membraną półprzepuszczalną, która może przepuszczać tylko cząsteczki rozpuszczalnika (rysunek 6).
Rysunek 6. Zjawisko osmozy i schemat działania osmometru.
Siłą napędową osmozy jest różnica potencjałów chemicznych rozpuszczalnika po obu stronach membrany. Po lewej stronie mamy czysty rozpuszczalnik, a więc jego potencjał chemiczny równy jest standardowemu. Po prawej stronie w roztworze, potencjał chemiczny rozpuszczalnika jest niższy, gdyż przy założeniu, że roztwór jest doskonały, wyraża się on wzorem :
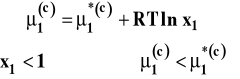
Wobec tego rozpuszczalnik będzie migrował przez membranę z lewa na prawo, aby wyrównać potencjały chemiczne po obu stronach. Jeśli po prawej stronie układu umieścimy cienką kapilarę, to w wyniku migracji rozpuszczalnika poziom cieczy w niej będzie się podnosił, tak długo aż ciśnienie hydrostatyczne słupa cieczy nie zahamuje procesu osmozy. Będzie to poszukiwane ciśnienie osmotyczne. Do pomiaru ciśnienia osmotycznego służą osmometry. Schemat ideowy osmometru jest pokazany na rysunku 6. Rzeczywiste konstrukcje są bardziej złożone. Pomiar ciśnienia osmotycznego musi być prowadzony w stałej temperaturze. Pomiary takie są długotrwałe, gdyż na ustalenie się równowagi osmotycznej trzeba czekać nawet kilka dni.
Proces osmozy będzie zachodził tak długo, aż potencjał chemiczny rozpuszczalnika przestanie się zmieniać.
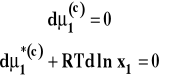
Na tej podstawie można wyprowadzić wzór opisujący ciśnienie osmotyczne (wyprowadzenie pomijamy) zwany wzorem van't Hoffa.
![]()
Stężenie c2 we wzorze to stężenie molowe wyrażone w mol/m3. Na podstawie pomiaru ciśnienia osmotycznego można wyznaczyć masę cząsteczkową substancji rozpuszczonej.
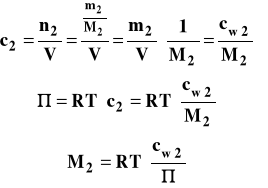
Z pośród metod wyznaczania masy cząsteczkowej przez pomiar wielkości koligatywnych tylko metoda osmometryczna nadaje się do wyznaczania mas cząsteczkowych substancji wielkocząsteczkowych - polimerów syntetycznych i naturalnych (białek, polisacharydów, itp.). Dlaczego tak jest, pozwoli nam wyjaśnić poniższy przykład.
Przykład
2 g polimeru o masie cząsteczkowej 200 000 g/mol rozpuszczono w 100 ml CCl4. Obliczyć obniżenie temperatury krzepnięcia roztworu oraz ciśnienie osmotyczne w temperaturze 25°C. Stała krioskopowa rozpuszczalnika 30 kg·K/mol, gęstość 1,63 g/cm3.
Rozwiązanie :
Aby obliczyć obniżenie temperatury krzepnięcia musimy najpierw obliczyć stężenie molarne roztworu polimeru.
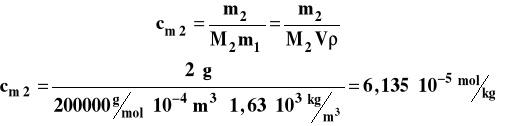
Obniżenie temperatury krzepnięcia wynosi więc :
![]()
Najlepsza dokładność termometrów wynosi zwykle ± 0,002 K, wobec tego zmiana temperatury, jaką mamy wyznaczyć, jest mniejsza od błędu pomiaru ! W takim układzie wyznaczenie masy cząsteczkowej jest praktycznie niemożliwe. Zauważmy, że w przykładzie mamy rozpuszczalnik o wyjątkowo dużej stałej krioskopowej. Zwykle jej wartość jest niższa, a więc i różnica temperatury krzepnięcia jest mniejsza.
Ciśnienie osmotyczne obliczymy następująco :
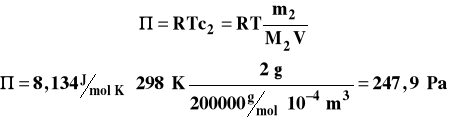
Po przeliczeniu na wysokość słupa cieczy, wyniesie ono :
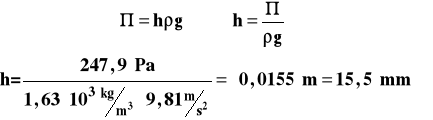
Taką wysokość słupa cieczy można już zmierzyć z zadowalającą dokładnością i błąd pomiaru będzie stosunkowo niewielki.
Wspólne cechy wielkości koligatywnych
Wielkość każdej z nich zależy tylko od ilości moli substancji rozpuszczonej wyrażonej jako stężenie w rozmaity sposób, a nie od rodzaju substancji rozpuszczonej.
Współczynnik proporcjonalności zależy tylko od własności rozpuszczalnika.
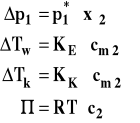
Wielkości koligatywne dla roztworów rzeczywistych
Wszystkie powyższe wzory zostały wyprowadzone przy założeniu doskonałości roztworów. Jeśli zmierzymy wielkości koligatywne dla roztworów rzeczywistych, to będą one miały zwykle inną wartość niż wynikałaby ona z powyższych wzorów. Jeśli weźmiemy na przykład NaCl czyli mocny elektrolit, to dysocjuje on w roztworze na dwa jony. W efekcie w roztworze jest dwa razy więcej indywiduów chemicznych (jonów) niż cząsteczek związku. W efekcie każda wielkość koligatywna będzie około dwa razy większa. Dlatego też do wzorów opisujących zachowanie roztworów rzeczywistych wprowadza się tak zwany współczynnik osmotyczny van't Hoffa (współczynnik izotoniczny) i.
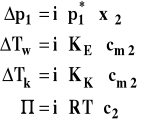
Można go zdefiniować jako stosunek doświadczalnie wyznaczonej wielkości koligatywnej do wartości obliczonej ze wzoru dla roztworu doskonałego.
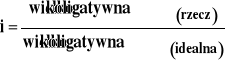
Na przykład :
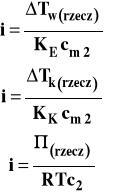
Można też współczynnik ten wyrazić jako stosunek masy cząsteczkowej formalnej (wynikającej z wzoru stechiometrycznego związku) do wyznaczonej doświadczalnie przez pomiar wielkości koligatywnych.
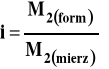
Wielkość współczynnika izotonicznego i zależy od :
stanu substancji rozpuszczonej w roztworze (jej dysocjacji jak w przypadku elektrolitów lub asocjacji)
od oddziaływań cząsteczek substancji rozpuszczonej z cząsteczkami rozpuszczalnika czyli odchyleń zachowania roztworu od doskonałości. Dla roztworów elektrolitów odchylenia od zachowania doskonałego są też spowodowane oddziaływaniami pomiędzy jonami.
Dla roztworów słabych elektrolitów (tylko i wyłącznie !) wyznaczenie współczynnika izotonicznego pozwala na obliczenie stopnia dysocjacji.
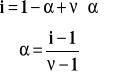
gdzie : - stopień dysocjacji - liczba jonów powstających w wyniku rozpadu jednej cząsteczki elektrolitu
Pomiar wielkości koligatywnych można wykorzystać do wielu celów. Można tu wymienić :
wyznaczanie masy cząsteczkowej substancji rozpuszczonej
wyznaczanie stopnia dysocjacji słabych elektrolitów lub też stopnia asocjacji substancji w roztworze, badanie równowag dysocjacji bądź asocjacji w roztworach
wyznaczanie współczynnika aktywności rozpuszczalnika
wyznaczanie współczynnika aktywności substancji rozpuszczonej
Sposoby wyznaczania masy cząsteczkowej i stopnia dysocjacji słabych elektrolitów zostały już omówione. W przypadku asocjacji związku w roztworze wielkość koligatywna będzie wyraźnie mniejsza niż dla roztworu doskonałego. Na podstawie obliczonej wartości współczynnika izotonicznego, można obliczyć wówczas stopień asocjacji. Ponadto poprzez pomiar obniżenia temperatury krzepnięcia lub podwyższenia temperatury wrzenia dla roztworu substancji o znanej masie cząsteczkowej można obliczyć stałe krioskopową bądź ebuliometryczną, a następnie wyznaczyć entalpię topnienia bądź parowania rozpuszczalnika.
Współczynnik aktywności rozpuszczalnika oblicza się ze wzoru :
![]()
Natomiast, aby obliczyć współczynnik aktywności substancji rozpuszczonej, należy zmierzyć wielkość koligatywną dla kilku różnych jej stężeń, poczynając od bardzo niskich (dążących do zera). Następnie trzeba dla każdego ze stężeń obliczyć współczynnik van't Hoffa i. Dla mocnych elektrolitów należy następnie obliczyć tak zwany współczynnik osmotyczny Bjerruma g :
![]()
Współczynnik aktywności znajduje się ze wzoru :
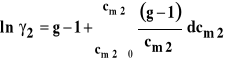
Dla roztworów nieelektrolitów oczywiście g = i. Potrzebną całkę wyznacza się zwykle w sposób graficzny (rysunek 7). Wartość poszukiwanej całki odpowiada polu pod krzywą na tym rysunku. Dla roztworów rozcieńczonych wartość całki w powyższym wzorze jest bardzo mała i może być pominięta. Współczynnik aktywności substancji rozpuszczonej można wówczas obliczyć w sposób przybliżony ze wzoru :
![]()
Rysunek 7. Wyznaczanie całki potrzebnej do obliczenia współczynnika aktywności substancji rozpuszczonej.
Własności (wielkości) koligatywne są to własności roztworów rozcieńczonych, których wartość zależy tylko od ilości (liczby moli, liczby cząsteczek) substancji rozpuszczonej przypadającej na określoną ilość rozpuszczalnika lub roztworu.
Względne obniżenie prężności pary rozpuszczalnika nad roztworem substancji nielotnej jest równe ułamkowi molowemu substancji rozpuszczonej w roztworze.
ciśnienie atmosferyczne
![]()
p
T
p1
![]()
Podwyższenie temperatury wrzenia roztworu substancji nielotnej w stosunku do czystego rozpuszczalnika jest wprost proporcjonalne do stężenia molarnego substancji rozpuszczonej, a współczynnik proporcjonalności (stała ebulioskopowa) zależy tylko od własności rozpuszczalnika.
![]()
Tt (roztwór)
Tt*
czysty stały rozpuszczalnik
rozpuszczalnik w roztworze
czysty ciekły rozpuszczalnik
p = const
T
Obniżenie temperatury krzepnięcia roztworu substancji tworzącej z rozpuszczalnikiem układ eutektyczny w stosunku do czystego rozpuszczalnika jest wprost proporcjonalne do stężenia molarnego substancji rozpuszczonej, a współczynnik proporcjonalności (stała krioskopowa) zależy tylko od własności rozpuszczalnika.
=p-po
p
po
kierunek migracji rozpuszczalnika
T = const
h
kapilara
membrana półprzepuszczalna (przepuszcza tylko cząsteczki rozpuszczalnika)
roztwór
czysty rozpuszczalnik
Osmoza to samorzutna migracja cząsteczek rozpuszczalnika od czystego rozpuszczalnika do roztworu przez membranę półprzepuszczalną w stałej temperaturze.
Ciśnienie osmotyczne, to ciśnienie, jakie należy przyłożyć do roztworu oddzielonego od rozpuszczalnika membraną półprzepuszczalną, aby zahamować całkowicie migrację rozpuszczalnika przez nią.
Ciśnienie osmotyczne roztworu jest wprost proporcjonalne do stężenia molowego roztworu, a współczynnik proporcjonalność zależy tylko od temperatury.
cm2
![]()
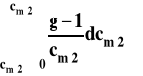
0