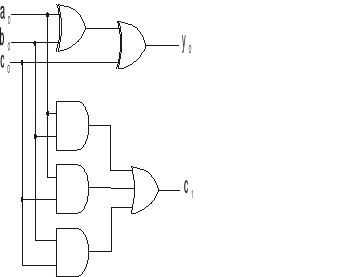
1. Układ głosujący 3 z 5

Warunkiem koniecznym i wystarczającym otrzymania „prawdy” (1) na wyjściu takiego układu jest wystąpienie trzech jedynek oraz dwóch zer w dowolnym ustawieniu.

Tablica prawdy dla takiego układu przyjmuje następującą postać

CDE AB	000	001	011	010	110	111	101	100
00	0	0	0	0	0	1	0	0
01	0	0	1	0	1	0	1	0
11	0	1	0	1	0	0	0	1
10	0	0	1	0	1	0	1	0

Z czego zapisujemy postać kanoniczną równania:

Y=

Dla uproszczenia wykonamy grupowanie wyrazów:

Y=

Korzystając z rozdzielności mnożenia względem dodawania oraz rozdzielności dodawania względem mnożenia otrzymujemy

następnie zgodnie z
(różnica symetryczna) oraz prawem DeMorgana
otrzymujemy

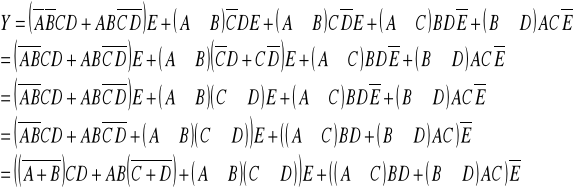
Schemat układu głosującego zrealizowany zgodnie z wyprowadzonym wzorem.

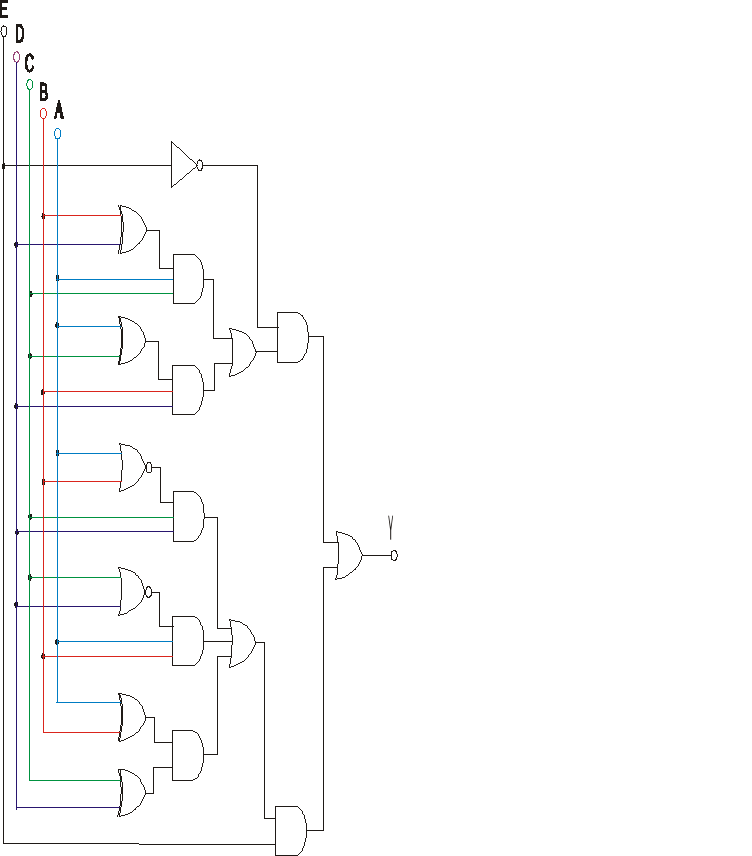
2. Sumator 2 bitowy

W układzie kombinacyjnym sumator 2 bitowy składa się z 2 sumatorów 1 bitowych.

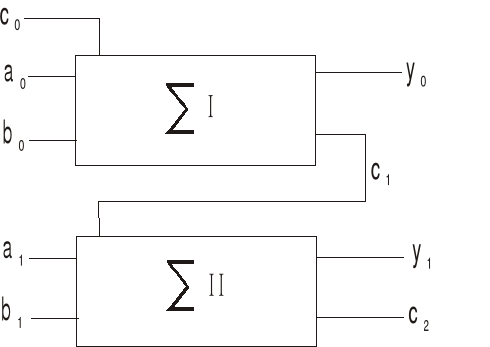
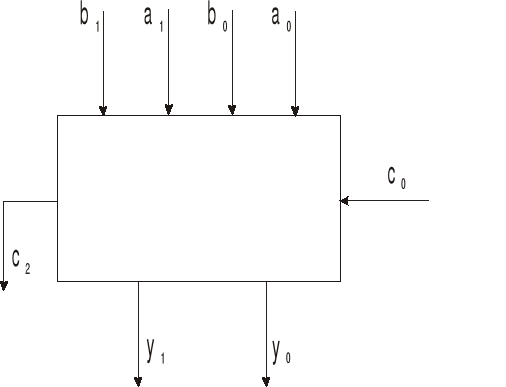
Zmienna y₀ reprezentuje rezultat operacji pierwszego sumatora, jej wartość jest sumą modulo 2 (exclusive OR) składników a₀, b₀ i c₀. Zmienna c₀ reprezentuje przeniesienie z pozycji młodszej sumatora wielopozycyjnego, c jest przeniesieniem do drugiego sumatora.

Zmienna y₁ reprezentuje rezultat operacji drugiego sumatora, jej wartość jest sumą modulo 2 składników a₁, b₁ i c₁, c₂ jest przeniesieniem do pozycji starszej sumatora wielopozycyjnego.

Tablice prawdy dla pierwszego sumatora 1 bitowego.

Tablica dla y₀

a0b0 c0	00	01	11	10
0	0	1	0	1
1	1	0	1	0

Z powyższej tablicy otrzymujemy wzór:

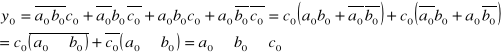
Tablica dla c₁

a0b0 c0	00	01	11	10
0	0	0	1	0
1	0	1	1	1

Z tablicy otrzymujemy zwór:

Schemat sumatora jednobitowego zbudowanego na podstawie równań.

Przekształcając powyższy wzór do postaci

można wyrazić w postaci: c_i+1= g_i+g_ic_i, gdzie: g_i=a_ib_i, t_i=a_i+b_i.
g - przeniesienie generowane w bloku,
t - sygnał warunkujący transmisję przeniesienia początkowego c₀.
Wyrażenie dla sumy y_i:

można przekształcić do postaci:

3. Zamek cyfrowy

Najprostszy zamek cyfrowy z jednym wejściem można stworzyć przy założeniu, że jeżeli na wejściu jest 1 to na wyjściu również otrzymujemy 1. Zastosowanie praktyczne takiego rozwiązanie jest jednak mało sensowne. Bardziej realnym rozwiązaniem jest stworzenie układu z większą ilością wejść, dającym na wyjściu 1 tylko przy jednej określonej kombinacji. Jeżeli jesteśmy
w stanie podać na wszystkie wejścia określone wartości zamek 4 wejściowy mógłby wyglądać następująco.

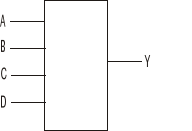
Załóżmy, że zamek otwiera się przy wartościach 1 na wejściach A i D, więc:

Z czego otrzymalibyśmy następujący układ.

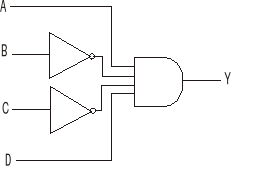
Stosunkowo prostym i skutecznym sposobem realizacji funkcji zamka jest zastosowanie dekodera z licznikiem. Znacznie zwiększa to ilość możliwych kombinacji, oraz pozwala na wprowadzenie sygnałów w określonej kolejności a nie jednocześnie (co byłoby szczególnie trudne w przypadku konieczności naciśnięcia jednoczenie kilku klawiszy). Dla podwyższenia skuteczności zamka można zastosować układ taktujący który wymusza wprowadzenie kolejnych cyfr w określonym czasie.

Założenia:

1. Zamek otwiera się po wprowadzeniu w odpowiedniej (jedynej możliwej) kolejności 6 określonych znaków

2. Znaki wprowadzane są w określonych odstępach czasów

3. Kod zamka jest ustawiany mechanicznie

4. Działanie zamka rozpoczyna się po naciśnięciu klawisz start.

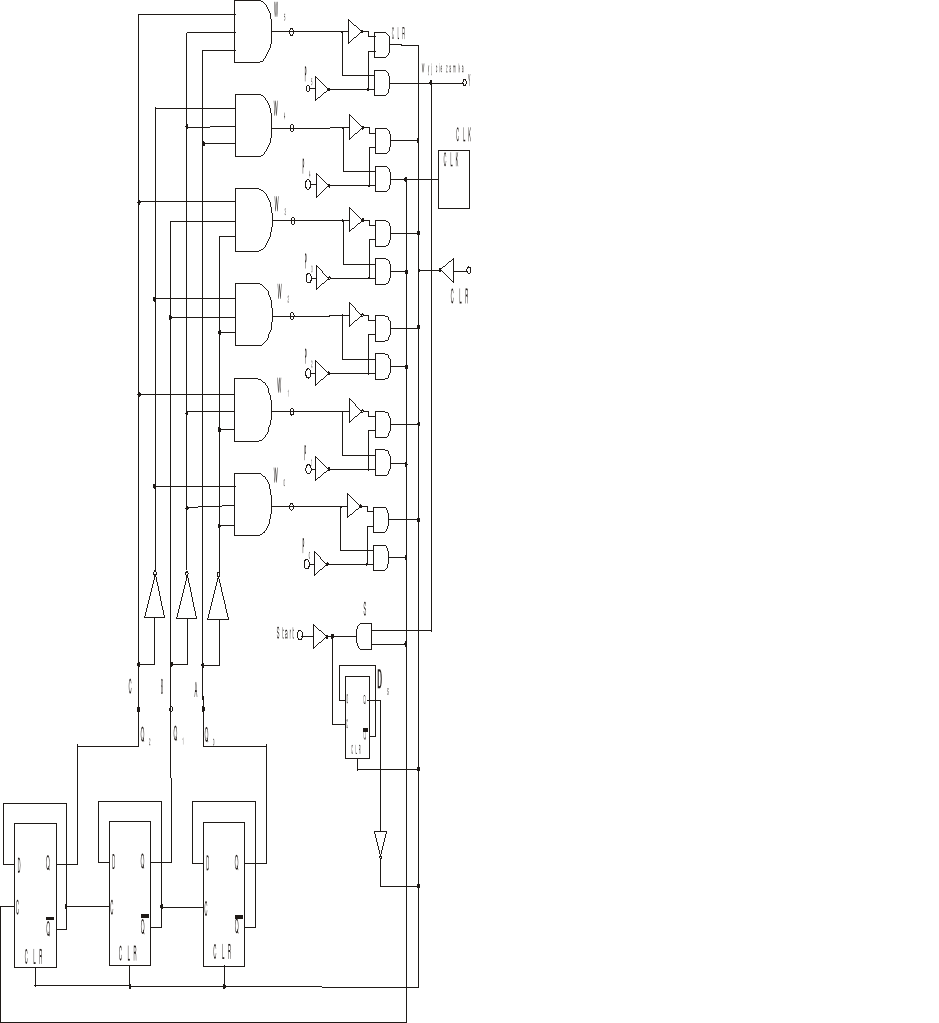
Do budowy zamka potrzebny będzie opis licznika oraz dekodera. Przy założeniu, że należy poprawnie wprowadzić 6 cyfr licznik musi być co najmniej modulo 6 (zliczający do 6).

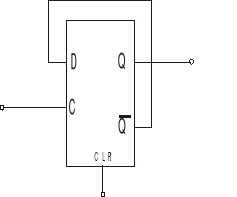
1. Licznik budujemy na dwójkach liczących realizowanych na przerzutnikach D

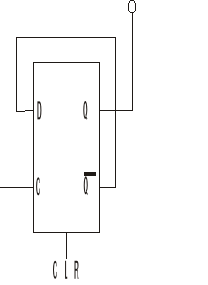
Ponieważ do wejścia D podłączone jest wyjście komplementarne Q przerzutnika, to przy każdym impulsie zegarowym stan wyjścia Q zmienia się na przeciwny.

CLR - zerowanie (reset).

Z dwójek liczących budujemy licznik modulo 6.

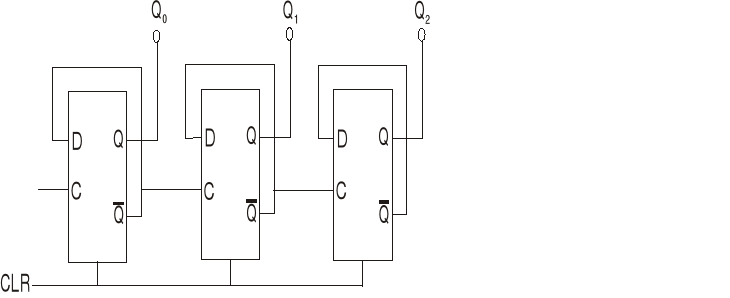
Stany licznika po opisuje tabela (n - kolejny takt, impuls wyzwalający)

n	Q2	Q1	Q0
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1

Z tabelki wyciągamy informację o tym, jaki stan powinien wystąpić na wejściu D każdego przerzutnika przed impulsem zegarowym, aby na wyjściach otrzymać stan następny. Możemy więc utworzyć tabelkę stanów wejść D w funkcji wyjść Q:

n	Q2	Q1	Q0	D2	D1	D0
0	0	0	0	0	0	1
1	0	0	1	0	1	0
2	0	1	0	0	1	1
3	0	1	1	1	0	0
4	1	0	0	1	0	1
5	1	0	1	0	0	0
6	0	0	0

Od impulsu 6 cykl się powtarza. Stany wejść D są funkcjami logicznymi stanów wyjść Q, co możemy zapisać następująco:

D₂ = d₂(Q₂, Q₁. Q₀)
D₁ = d₁(Q₂, Q₁. Q₀)
D₀ = d₀(Q₂, Q₁. Q₀)

Przy pomocy odpowiednich map Karnaugha utworzonych zgodnie z powyższą tabelką, znajdujemy postać ww. funkcji. Warto zauważyć że, stanu 111 licznik nigdy nie osiąga, więc można tam wpisać dowolną wartość. Wykorzystamy to, by uprościć maksymalnie funkcje przełączania przerzutników.

Q1Q0 Q2	00	01	11	10
0	1	0	0	1
1	1	0	0	1

D₀

czyli

Q1Q0 Q2	00	01	11	10
0	0	1	0	1
1	0	0	0	1

D₁

czyli

Q1Q0 Q2	00	01	11	10
0	0	0	1	0
1	1	0	1	1

D₂

czyli

Drugim elementem zamka jest dekoder. Układ wybierający na podstawie adresu. Dekoder musi mieć tyle wejść ilu bitowy jest adres (pośrednio: ile cyfr zaprojektowaliśmy). W naszym przypadku adres będzie 3 bitowy. Układ powinien działać wg. poniższej tabeli tzn. stan wysoki (1) otrzymujemy na określonym przez adres wyjściu, na pozostałych stan niski (0).

A	B	C	W0	W1	W2	W3	W4	W5
0	0	0	1	0	0	0	0	0
0	0	1	0	1	0	0	0	0
0	1	0	0	0	1	0	0	0
0	1	1	0	0	0	1	0	0
1	0	0	0	0	0	0	1	0
1	0	1	0	0	0	0	0	1

z tabeli otrzymujemy:

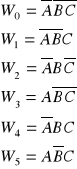
Dzięki jednoznacznemu określeniu wyjścia, które jako jedyne znajduje się wstanie wysokim możemy zbudować układ zamka, zgodnego z pierwotnymi założeniami. Po naciśnięciu klawisz start na klawiaturze następuje uruchomienie licznika, dla uproszczenia zakładamy kod 0,1,2,3,4,5, możliwa jest każda inna kombinacja po zmianie połączeń linii adresowych między licznikiem
i dekoderem), otrzymujemy sytuację:

• jeżeli następnym przyciskiem będzie 0 licznik zwiększ się o 1 i oczekuje na wciśnięcie następnej cyfry

• jeżeli znak nie był 0, układ się resetuje, bez monitowania (nie informuje wprowadzającego kod, o błędzie)

Sytuacja powtarza się do czasu wprowadzenia w odpowiedniej kolejności 6 znaków. W ytakiej sytuacji na ostatnim wyjściu dekodera otrzymujemy 1 czyli otwarcie zamka.

Układ dekodera adresowanego 3 bitami (ABC) z przedstawionego wcześniej licznika:

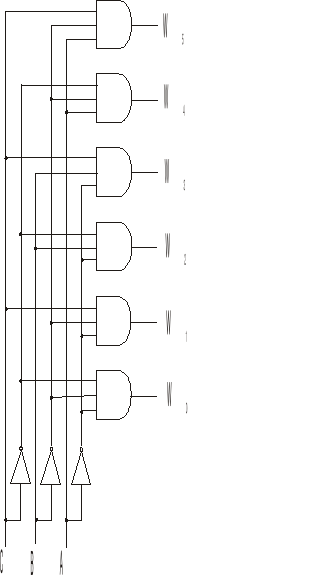
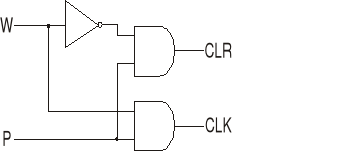
Ponieważ tylko jedno z wyjść jest w stanie wysokim w danym momencie należy sprawdzić czy wybrany przycisk odpowiada wyjściu licznika i jeżeli tak to zwiększyć jego wartość a jeżeli nie wyresetować zamek. P - przycisk (wciśnięty -1, wolny - 0), CLK - licznik (sygnał taktujący)

W	P	CLK	CLR
0	0	0	0
0	1	0	1
1	0	0	0
1	1	1	0

Z połączenia układów otrzymujemy:

Rozpoczęcie działania zamka następuje po naciśnięciu klawisza start. Wybieranie kolejnych cyfr następuje przy kolejnych zwarciach końcówek P do masy (zastosowany inwerter). W przypadku pomyłki można wyresetować układ przez zwarcie przycisku CLR do masy. Układ taktujący (CLK) wysyła impulsy co określony czas, jeżeli na jego wyjściu nie pojawił się stan wysoki spowodowany zwarciem odpowiedniej końcówki P do masy.

Jedyną możliwością przejścia licznika do ostatniego stanu (101) jest zwieranie w odpowiedniej kolejności końcówek P do masy, w wyniku czego na wyjściu Y pojawia się stan wysoki (może sterować ryglem zamka). Ponieważ układ taktujący cały czas pracuje po określonym czasie wyśle impuls, co spowoduje otwarcie bramki S i zmianę stanu licznika D_s. na niski, zresetowanie układu, na wyjściu Y pojawi się stan niski czyli zamek zostaje zamknięty.

Zmiany kodu otwierającego zamek można dokonać poprzez zmianę kolejności połączeń wyjść licznika i wejść adresowych dekodera oraz odpowiednią zmianę wyjścia Y zamka. Dołożenie większej ilości stopni licznika i dekodera zwiększa ilość kombinacji zamka.

4. Układ wykrywający nieparzystą ilość jedynek.

Układ powinien sprawdzać czy wprowadzona w ciągu liczba jedynek jest nieparzysta.

n - liczba jedynek

n	y
0	0
2n	0
2n-1	1

Skorzystamy z faktu, że jeżeli do wejścia zegarowego pojedyńczego licznika doprowadzimy jedynkę zmienia stan na przeciwny. Zakładając, że licznik na początku jest wyzerowany to jeżeli wyjście jest w stanie wysokim wystąpiła nieparzysta liczba jedynek, jeżeli jest w stanie niskim liczba jedynek byłą parzysta lub jedynek nie było.

Tablica prawdy dla przerzutnika dwójki liczącej

C	Qn
0	Qn
1	Qn-1

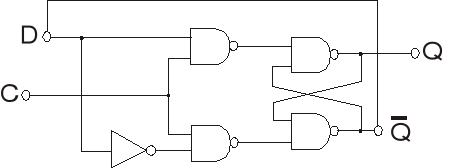
Tak zbudowany układ nazywany jest dwójką liczącą, symbol graficzny takiej dwójki przestawia rysunek:

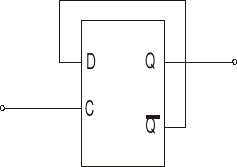
Aby mieć pewność jaki stan występował na początku zliczania należy użyć dwójki liczącej
z wejściem resetującym. Po zresetowaniu na wyjściu Q licznika pojawia się stan niski. Kolejne impulsy zegarowe podawane na wejście C, w naszym przypadku jedynki z wprowadzanego ciągu, zmieniają stan wyjścia licznika na przeciwny. Czyli zakładając, że na początku wyjście Q było
w stanie niskim nieparzysta liczba jedynek była wprowadzona jeżeli wyjście Q jest w stanie wysokim.

---