Łuk kołowy z niesymetrycznymi klotoidami.

Klotoida, czyli krzywa przejściowa stosowana jest, by siła odśrodkowa podczas wyjazdu z łuku kołowego była wyprowadzana wolniej. Dla każdego promienia R można określić minimalną długość L krzywej przejściowej zależnie od dopuszczalnej prędkości v, i następnie z równania L ⋅ R = a², znając w nim dwie wartości, określić trzecią, czyli parametr a klotoidy. Uogólniając można stwierdzić, że im większy promień R, tym mniejsza siła odśrodkowa i tym krótszą krzywą przejściową można stosować, a dla bardzo dużych promieni nawet zupełnie ją pominąć.

Ze względu na ukształtowanie terenu w niektórych przypadkach konieczne jest zastosowania 2 różnych klotoid przy danym łuku kołowym. Mamy wtedy do czynienia z łukiem kołowym z niesymetrycznym klotoidami.

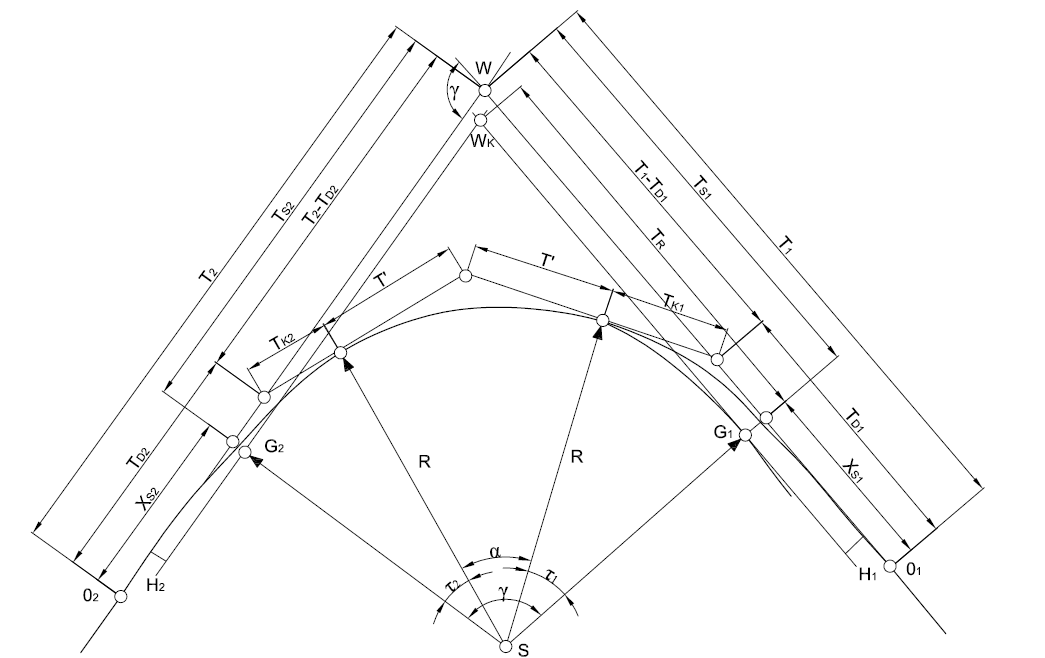
Związki geometryczne w łuku kołowym z dwiema niesymetrycznymi klotoidami. Rys.1

WYZNACZENIE PUNKTÓW GŁÓWNYCH ŁUKU KOŁOWEGO Z NIESYMETRYCZNYMI KLOTOIDAMI.

Punkty główne klotoidy są to punkty styczności z prostą z jednej strony i z łukiem kołowym z drugiej. Wyznaczenie ich w terenie jest wykonywane, podobnie jak dla łuku kołowego, na podstawie znajomości położenia punktu wierzchołkowego oraz kierunków głównych trasy.

Przystępując do obliczeń, kąt γ dzielimy na 3 części:

Dane:

Korzystając ze wzorów:
można zapisać
, patrząc na rys.2 można więc uznać, że:

, jeżeli
to:

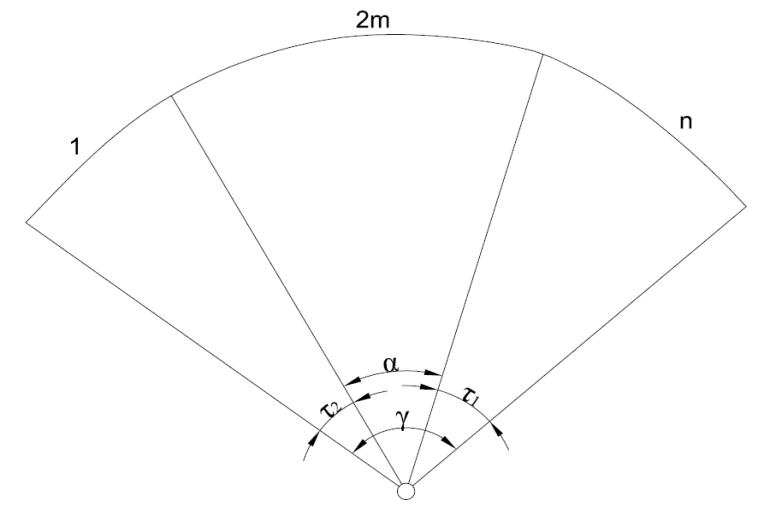
Postępując analogicznie otrzymamy:

rys.2

Jeżeli

,
,
, a więc:

Po rozdzieleniu kąta γ na 3 części, z wielkości R i τ₁ wyznaczamy parametr pierwszej klotoidy, a z wielkości R i τ₂ - parametr drugiej klotoidy.

Na podstawie τ₁ wyznaczamy elementy jednostkowe klotoidy pierwszej l₁, x₁, y₁ itd. Parametr a₁ obliczamy z zależności a₁=Rl₁ i mnożąc przez niego elementy jednostkowe otrzymujemy L₁, X, Y, X_s, H,… Podobnie znajdujemy wszystkie dane potrzebne do wyznaczenia drugiej klotoidy.

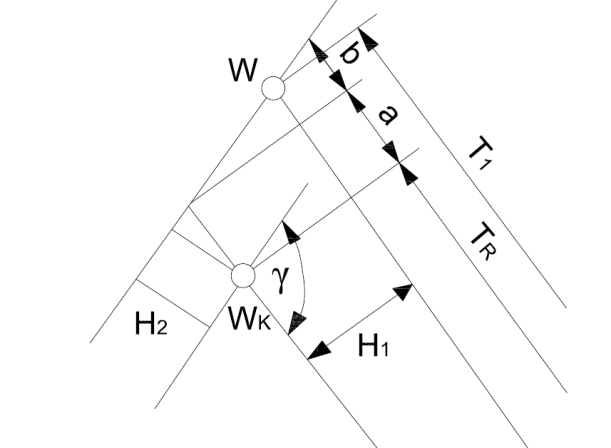
Wyznaczenie T₁ i T₂.

Z rys.1 wynika że:

Patrząc na rys3. możemy napisać: rys.3

czyli

Ostatecznie otrzymujemy:

---