1

A.Jednoróg – SPC

ZBIERANIE DANYCH

SPC

Adam Jednoróg

A.Jednoróg – SPC

2

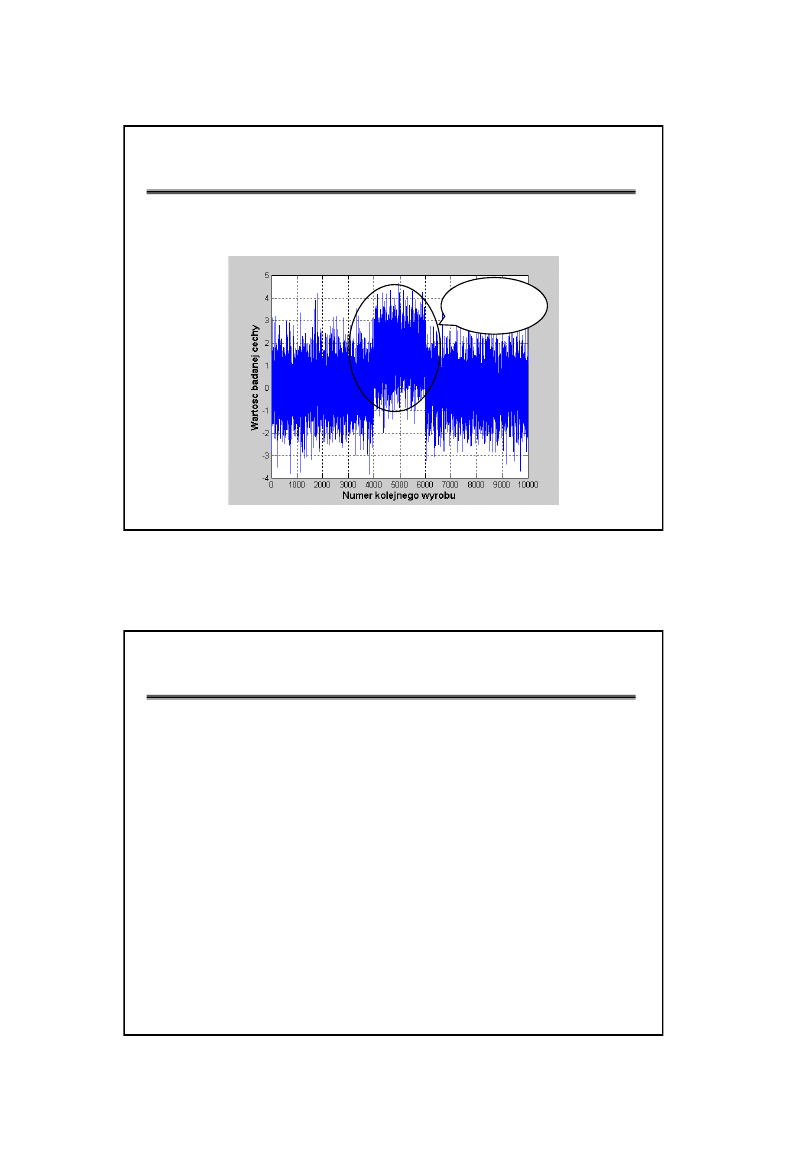
STANY PROCESU

• Stan statystycznie stabilny (uregulowany)

– zmienność własna procesu (naturalna, szum)

2

A.Jednoróg – SPC

3

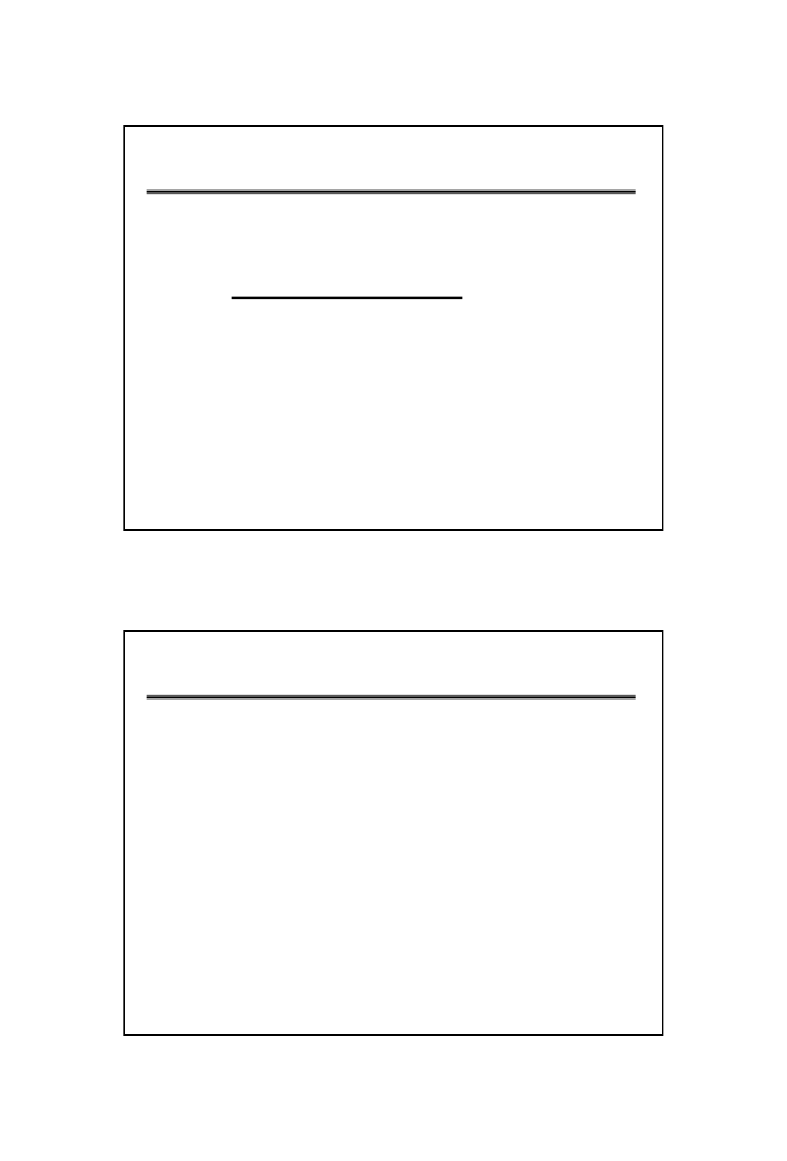
STANY PROCESU

• Stan statystycznie niestabilny (nieuregulowany)

– zmienność całkowita procesu

Działanie

przyczyn

specjalnych

A.Jednoróg – SPC

4

W zależności od tego jakie zmienności występują w procesie, można mówić o:
•

Stanie statystycznie uregulowanym (ang. state of statistical control)

– jest to stan, w którym

zmienność między obserwowanymi wynikami badania próbki może być przypisana zespołowi

przyczyn losowych i który nie ulega zmianom w czasie. Taki zespół przyczyn losowych

odzwierciedlany jest przez wyniki otrzymane z próbek losowych prostych pobranych z populacji.

•

Stanie statystycznie nieuregulowanym, w stanie niestabilnym (ang. state out of statistical
control)

– jest to stan, w którym obok przyczyn losowych występują również przyczyny specjalne

[PN-ISO 3534-2:1994]

Proces, w którym każda z miar jakości (np. wartość średnia i rozrzut lub frakcja jednostek niezgodnych

lub liczba niezgodności wyrobu) jest w stanie statystycznie uregulowanym nazywany jest proces
uregulowanym lub procesem stabilnym (ang. proces in control, stable proces).

Gdy proces znajduje się w stanie statystycznie uregulowanym, to jego zmienność lub zmienność

wytwarzanych przez niego wyrobów określana jest jako zmienność własna procesu (ang.

inherent process variability). Zmienność własna procesu określana na podstawie procesu

jednostkowego (jedno urządzenie lub linia produkcyjna, jedna grupa operatorów, jedna partia

materiału) jest zwykle mniejsza od tej zmienności określanej dla procesu ogólnego (wiele

urządzeń lub linii produkcyjnych, grup operatorów i partii materiału).

Do określenia zmienności własnej stosowane jest też pojęcia zmienności naturalnej czy białego

szumu.

Zmienność procesu obejmująca zmienność własną i zmienność spowodowaną przez inne czynniki

prowadzące do zmian, takie jak błędy operatora, źle uregulowane lub uszkodzone urządzenia,

użycie materiału niezgodnego ze specyfikacją, błędy systematyczne lub inne dające się określić
przyczyny, nazywana jest

całkowitą zmiennością procesu (ang. total process variability)

3

A.Jednoróg – SPC

5

KARTY KONTROLNE SHEWHARTA

• CEL:

– Porównać stan bieżący stan procesu

ze

zmiennością własną procesu, a

NIE TYLKO ZE SPECYFIKACJAMI!

– Odróżnić to co losowe w procesie

od tego co jest specjalne

– Jak najszybciej wykryć nienaturalne

zmienności procesu

A.Jednoróg – SPC

6

KARTY KONTROLNE SHEWHARTA

Pomagają:
1.

Wstępnie ocenić stan procesu.

2.

Wykryć stany niestabilności procesu i
wyeliminować ich przyczyny.

3.

Ustabilizować proces.

4.

Utrzymać proces w stanie statystycznie
stabilnym (zapewnić status quo)

5.

Redukować zmienność procesu.

4

A.Jednoróg – SPC

7

Karta kontrolna (ang. control chart) jako metoda graficzna o zasadniczym znaczeniu dla sterowania produkcją została

zaproponowana przez dr Waltera Shewharta w 1924 r. Jest to graficzna metoda prezentowania i porównywania

informacji pochodzących z ciągu próbek reprezentujących bieżący stan procesu z granicami wynikającymi z

uwzględnienia jego zmienności własnej.

Karta kontrolna (ang. control chart)

– wykres z zaznaczoną górną i/lub dolną granicą kontrolną, na którym rejestrowane

są wartości pewnej miary statystycznej, uzyskane z serii próbek lub podzbiorów, zwykle w porządku ich

występowania w czasie lub w porządku numerów próbki. Często na karcie występuje linia centralna, która ułatwia

śledzenie trendu, jaki wykazują rejestrowane wartości względem granic kontrolnych. [PN-ISO 3534-2:1994]

Zasadniczym celem kart kontrolnych jest jak najszybsze wykrywanie nienaturalnych zmienności w danych

otrzymywanych z powtarzalnych procesów. Karty kontrolne dostarczają kryteria dla wykrywania braku

statystycznego uregulowania procesu. Mogą one być również stosowane do szacowania parametrów procesu

produkcyjnego i przez to, do określania zdolności procesu (ang. process capability).

Granice kontrolne, to granice pomiędzy którymi z bardzo dużym prawdopodobieństwem znajduje się wartość

rozpatrywanego parametru statystycznego, jeżeli proces znajduje się w stanie statystycznie uregulowanym.

Shewhart zaproponował, by granice kontrolne były ustalane na poziomie +/- 3 po każdej stronie linii centralnej, co

odpowiada wartości współczynnika k=3. Przy granicach +/- 3 , około 99,73 % wartości z próbek znajdzie się w

granicach kontrolnych, przy założeniu, że proces jest statystycznie uregulowany. W takim przypadku ryzyko

popełnienia błędu I rodzaju wynosi 0,27 %, czyli w średnio 3 punkty na tysiąc mogą znaleźć się poza granicami
kontrolnymi, gdy proces jest stabilny.

Shewhart zdawał sobie sprawę z faktu, że w praktyce popełnia się oba rodzaje błędów i należy dążyć do osiągnięcia

minimalnych strat wynikających z tych błędów. Zaproponowane przez niego granice na poziomie +/- 3 dają, w

szerokim zakresie nieznanych warunków, racjonalną i ekonomiczną wskazówkę do osiągnięcia minimalnych strat

wynikających z obu rodzajów błędów.

A.Jednoróg – SPC

8

Ogólny model kart kontrolnych

• Niech:

w

– statystyka testowa określająca badany parametr

jakościowy (np. wartość średnia)

k

– odległość granic kontrolnych od linii centralnej

wyrażona w odchyleniach standardowych

• Granice kontrolne:

UCL =

w

+ k

W

CL =

w

LCL =

w

- k

W

5

A.Jednoróg – SPC

9

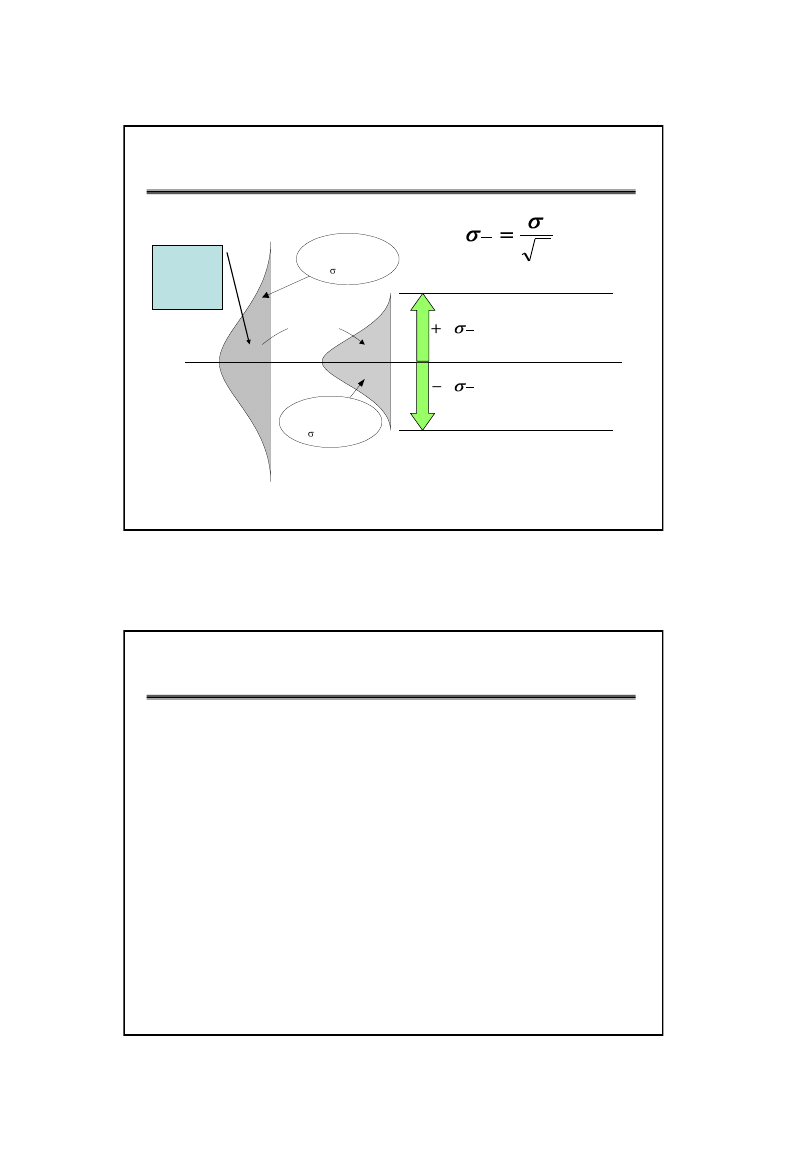
Karta wartości średnich

Górna granica kontrolna UCL

Dolna granica kontrolna LCL

Linia centralna CL

Rozkład wartości

indywidualnych

= 0.01

Rozkład wartości

srednich z próbek

= 0.0045

Próbka n=5

Badany

parametr:

wartość

średnia

n

X

X

3

X

3

A.Jednoróg – SPC

10

Karta z wartościami normatywnymi

• Wartości normatywne mogą być określane na

podstawie:

– obserwacji i dotychczasowego doświadczenia z

nadzorowania procesu

– określonych wartości normatywnych (np. wartość

zadana, tolerancje)

– przesłanek ekonomicznych (np. kosztów zgodności i

kosztów niezgodności)

• Zaleca się, aby wartości normatywne były

zgodne z naturalną zmiennością procesu

W przeciwnym razie może dojść do zjawiska

PRZEREGULOWANIA PROCESU

6

A.Jednoróg – SPC

11

Karta X-R

• Założenia:

– Zmienność podlega rozkładowi normalnemu
– Badana jest jedna właściwość (cecha)
– Granice kontrolne powinny być wyznaczone

na podstawie przebiegu procesu, który jest w
stanie statystycznie stabilnym

– Kolejne wyniki pomiarów muszą być

niezależne (brak autokorelacji)

A.Jednoróg – SPC

12

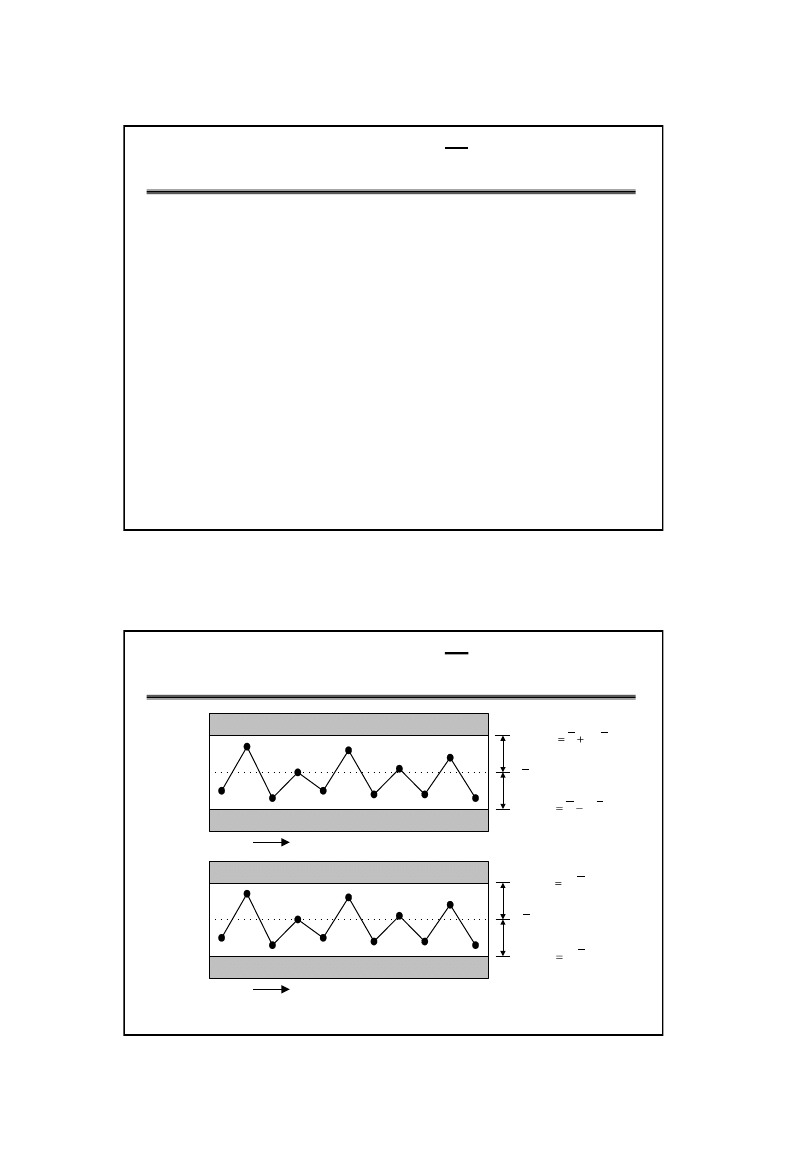
Karta kontrolna X-R

• W mniej więcej regularnych odstępach

pobieraj n-

elementowe próbki z procesu

– kategorie czasowe (np. 3 jednostki co

godzinę)

– kategorie ilościowe (np. 3 na 50 jednostek)

• Dla każdej próbki oblicz:

– wartość średnią z próbki
– oraz rozstęp jako różnica między największą i

najmniejszą wartością w próbce

R

i

= X

max

- X

min

i

X

7

A.Jednoróg – SPC

13

KARTA X-R

•

Postępowanie:

1.

Zebrać i przeanalizować dane obliczając
średnie i rozstępy

2.

Wykreślić i przeanalizować kartę R

3.

Wykreślić i przeanalizować kartę X

4.

Jeśli wykres nie wykazuje przebiegów
nielosowych, to wyznaczone granice
kontrolne można zastosować do
nadzorowania procesu w przyszłości

A.Jednoróg – SPC

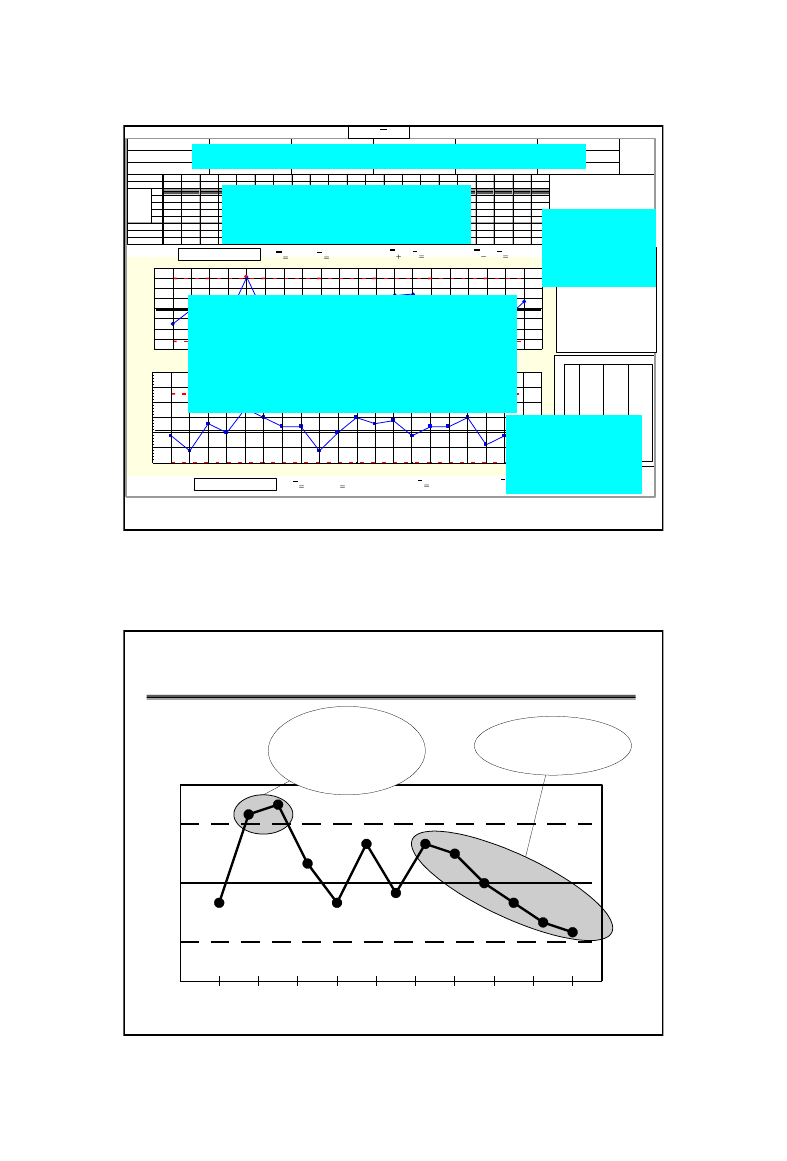
14

KARTA X-R

R

A

X

UCL

2

Czas

Czas

X

R

R

D

UCL

4

R

D

LCL

3

X

R

R

A

X

LCL

2

8

A.Jednoróg – SPC

15

13.01

13.01

14.01

14.01

15.01

15.01

16.01

16.01

17.01

17.01

06:30

13:15

06:30

13:15

06:30

13:15

06:30

13:15

06:30

13:15

6.01

6.01

7.01

7.01

8.01

8.01

9.01

9.01

10.01

10.01

06:30

13:15

06:30

13:15

06:30

13:15

06:30

13:15

06:30

13:15

12,67

12,66

12,66

12,59

12,76

12,68

12,63

12,59

12,61

12,71

12,62

12,68

12,74

12,67

12,7

12,63

12,63

12,57

12,63

12,64

12,59

12,64

12,68

12,62

12,79

12,73

12,68

12,64

12,65

12,67

12,59

12,67

12,63

12,69

12,61

12,58

12,56

12,62

12,65

12,61

12,68

12,64

12,61

12,65

12,75

12,61

12,56

12,69

12,62

12,63

63,15

63,29

63,32

63,22

63,61

63,23

63,06

63,11

63,16

63,26

12,630

12,658

12,664

12,644

12,722

12,646

12,612

12,622

12,632

12,652

0,09

0,04

0,13

0,1

0,18

0,15

0,12

0,12

0,04

0,1

12,58

12,60

12,62

12,64

12,66

12,68

12,70

12,72

12,74

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

0,00

0,05

0,10

0,15

0,20

0,25

0,30

Działania korygujące podjąć w

przypadku:

1.Punkty poza granicami

kontrolnymi.

2. 7 kolejnych punktów

w znoszących się lub

opadających.

3. 7 punktów pod lub nad linią

centralną.

4. Inny w idoczny przebieg

nielosow y.

Maszyna: SIGMAT

Zakład:

Maszyna: P2.21.36.006

Operacja: 30

Numer rysunku: 4271101

Nazwa części: Półoś napędowa

Właściw ość:

Tolerancja górna= 12.75

Tolerancja dolna= 12.45

Nominał= 12.06

Nr urz. pom.:

Nazw a urz. pom.:

Jed. miary:

Wielkość próbki= 5

Częstotliw ość= 2/zmianę

Poprz. średnia=

Poprz.LCL=

Poprz.UCL=

Numer
karty:

n
2
3
4
5
6
7
8
9

10

A

2

1,88
1,02
0,73
0,58
0,48
0,42
0,37
0,34
0,31

D

3

-
-
-
-
-

0,08
0,14
0,18
0,22

D

4

3,27
2,57
2,28
2,11
2,00
1,92
1,86
1,82
1,78

Karta -R

X

X średnie

X średniaX

LCL = X A R

2

UCL = X A R

2

12.658

12.596

12.720

UCL = D R

4

R średniaR

LCL = D R

3

Rozstępy

0.108

0.228

0

UWAGA:

Nie należy ingerow ać w

proces, bez pew ności, że

w ystąpiły zakłócenia specjalne.

Notow ać w szelkie zmiany w

procesie (ludzie, narzędzia,

materiał, metoda, otoczenie).

Użyć odw rotnej strony kartki w

celu zapisania następujących

informacji:

- numer próbki,

- co, jak i dlaczego się stało,

- jak zostało popraw ione,

- kto w prow adził zmiany.

12,69

12,73

12,72

12,671

12,661

12,68

12,6

12,65

12,64

12,68

12,66

12,6

12,61

12,661

12,741

12,73

12,68

12,61

12,7

12,66

12,56

12,71

12,67

12,661

12,651

12,74

12,67

12,64

12,64

12,69

12,66

12,73

12,75

12,701

12,631

12,63

12,67

12,67

12,61

12,69

12,71

12,61

12,68

12,751

12,621

12,62

12,75

12,62

12,61

12,65

63,28

63,38

63,43

63,445

63,305

63,4

63,37

63,19

63,2

63,37

12,656

12,676

12,686

12,689

12,661

12,680

12,674

12,638

12,640

12,674

0,15

0,13

0,14

0,09

0,12

0,12

0,15

0,06

0,09

0,04

Data

Czas

P

om

ia

ry

w

p

ró

bc

e

1

5

4

3

2

Suma

Średnia

Rozstęp

Część informacyjna (BIURO/OPERATOR)

Pomiary / obliczenia -

OPERATOR

Wykreślanie punktów i

interpretacja/ podejmowanie

decyzji - OPERATOR

Interpretacja i

podejmowanie

decyzji -

OPERATOR

Dokumentowanie

(na drugiej

stronie) -

OPERATOR

A.Jednoróg – SPC

16

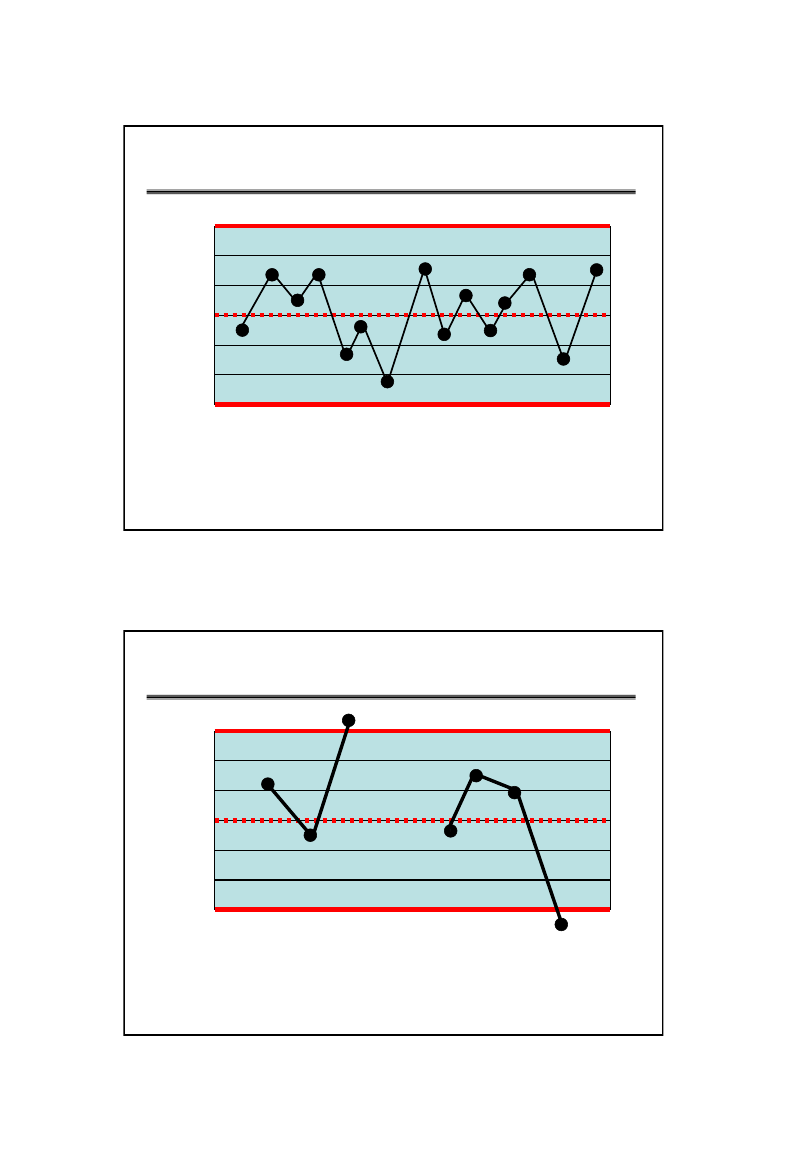
ANALIZA KART KONTROLNYCH

Dolna granica kontrolna (LCL)

Górna granica kontorlna (UCL)

Linia
ce ntralna

1

2

3

4

5

6

7

8

9

10

C

e

c

h

a

j

a

k

o

ś

c

io

w

a

Działanie przycyzn

specjalnych

punkty poza granicami

kontrolnymi

Działanie przyczyn

specjalnych

nielosowy przebieg, w zór

9

A.Jednoróg – SPC

17

C

B

A

ANALIZA KART KONTROLNYCH

• Przebieg losowy, normalny

– Brak charakterystycznych wzorów

A

B

C

UCL

LCL

CL

A.Jednoróg – SPC

18

C

B

A

A

B

C

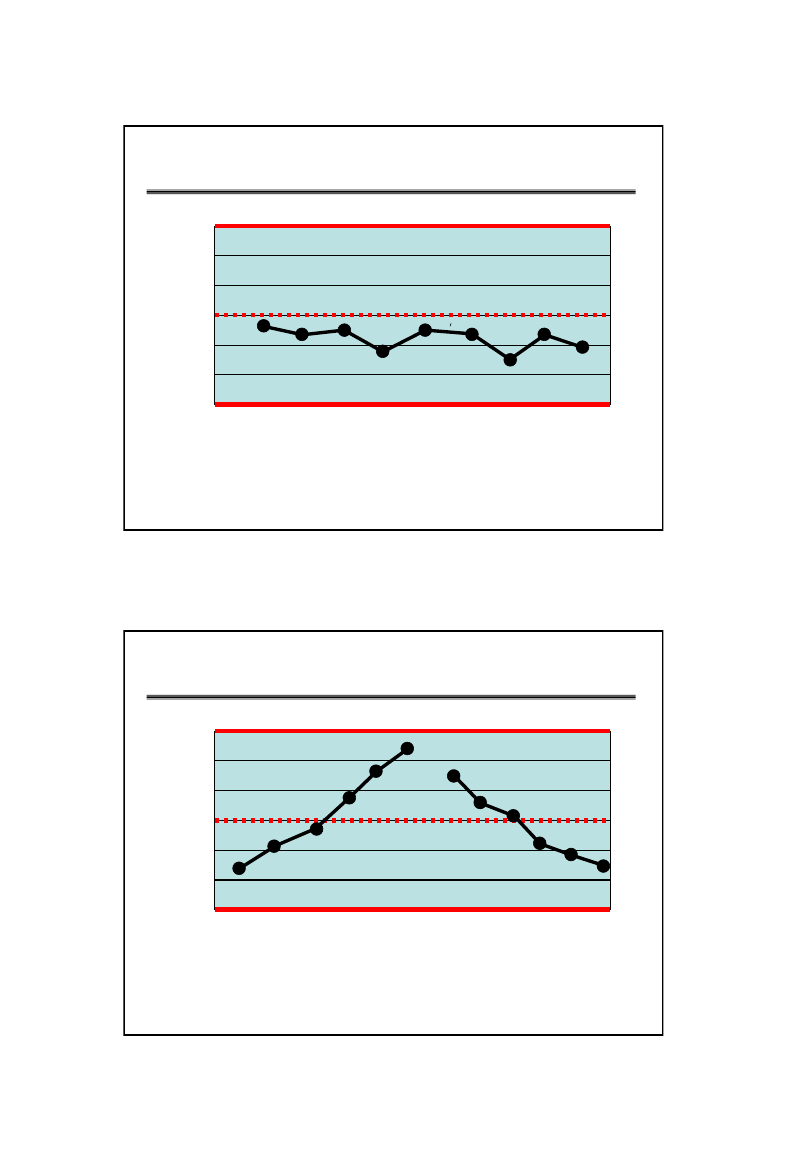
TEST 1

• Jeden punkt poza strefą A

UCL

LCL

CL

10

A.Jednoróg – SPC

19

C

B

A

A

B

C

TEST 2

• 9 kolejnych punktów w strefie C lub poza nią

po tej samej stronie linii centralnej

UCL

LCL

CL

A.Jednoróg – SPC

20

C

B

A

A

B

C

TEST 3

• Trend

– 6 kolejnych punktów stale rosnących i opadających

UCL

LCL

CL

11

A.Jednoróg – SPC

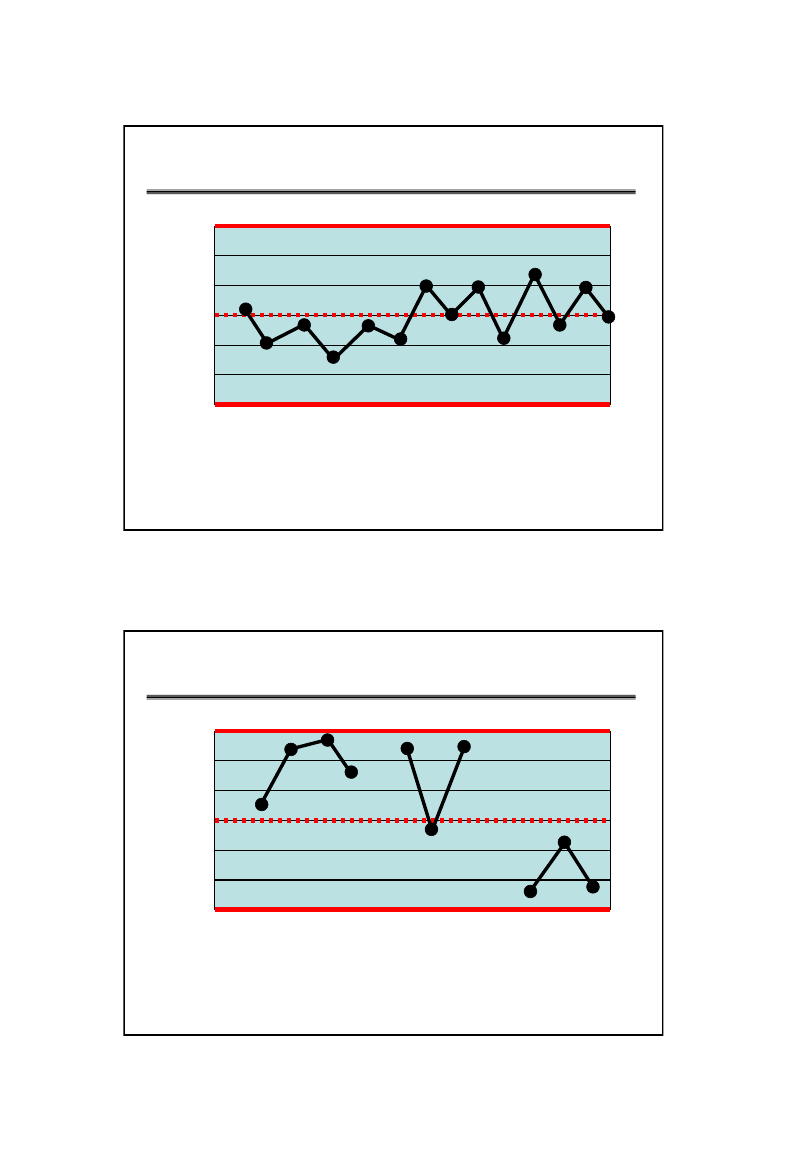
21

C

B

A

A

B

C

TEST 4

• 14 punktów po kolei przemiennie

rosnących i malejących

UCL

LCL

CL

A.Jednoróg – SPC

22

C

B

A

A

B

C

TEST 5

• 2 z 3 kolejnych punktów w strefie A lub

poza nią

UCL

LCL

CL

12

A.Jednoróg – SPC

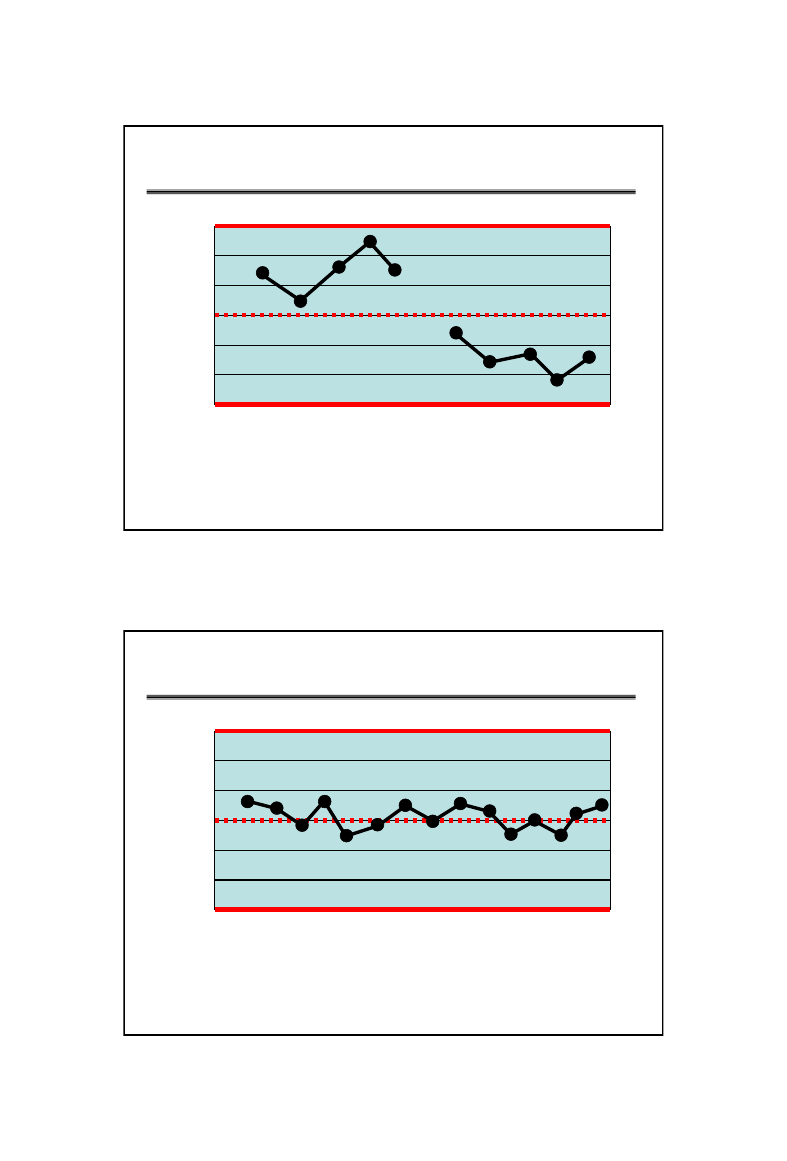
23

C

B

A

A

B

C

TEST 6

• 4 z 5 kolejnych punktów w strefie B lub

poza nią

UCL

LCL

CL

A.Jednoróg – SPC

24

C

B

A

A

B

C

TEST 7

• 15 kolejnych punktów w strefie C

powyżej lub poniżej linii centralnej

UCL

LCL

CL

13

A.Jednoróg – SPC

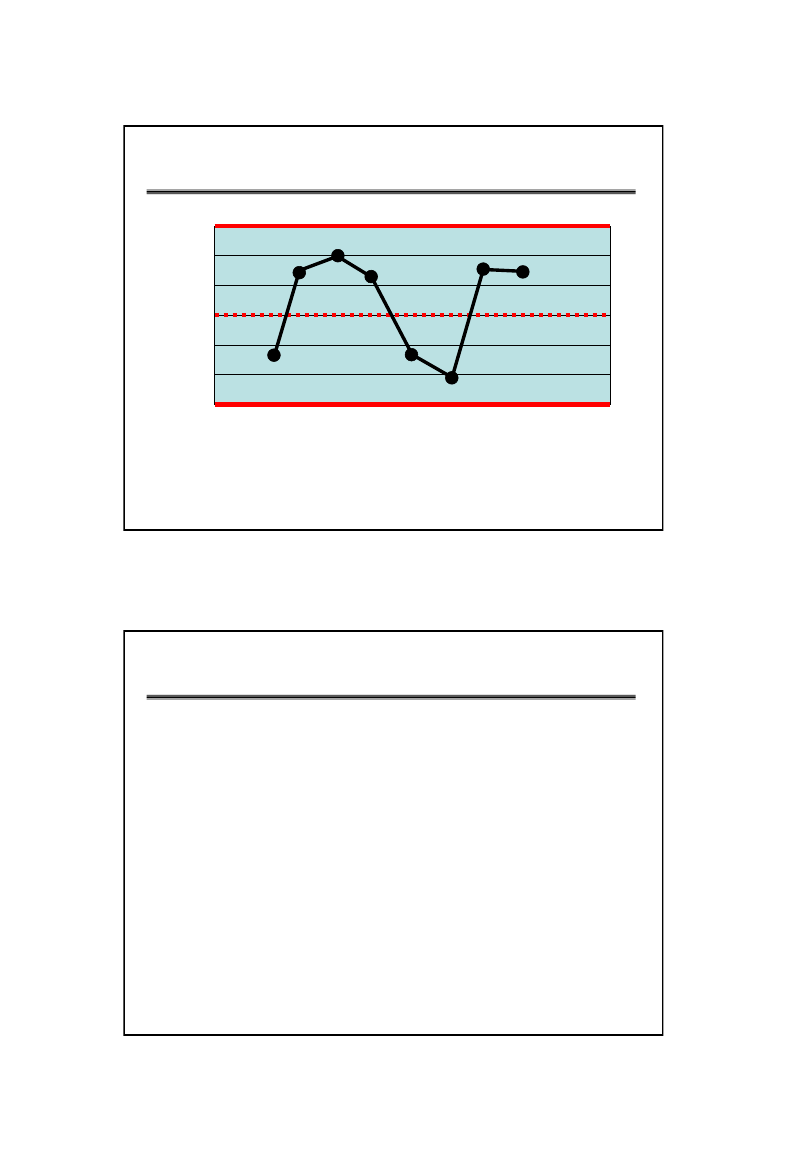
25

C

B

A

A

B

C

TEST 8

• 8 kolejnych punktów po obu stronach linii

centralnej lecz żaden w strefie C

UCL

LCL

CL

A.Jednoróg – SPC

26

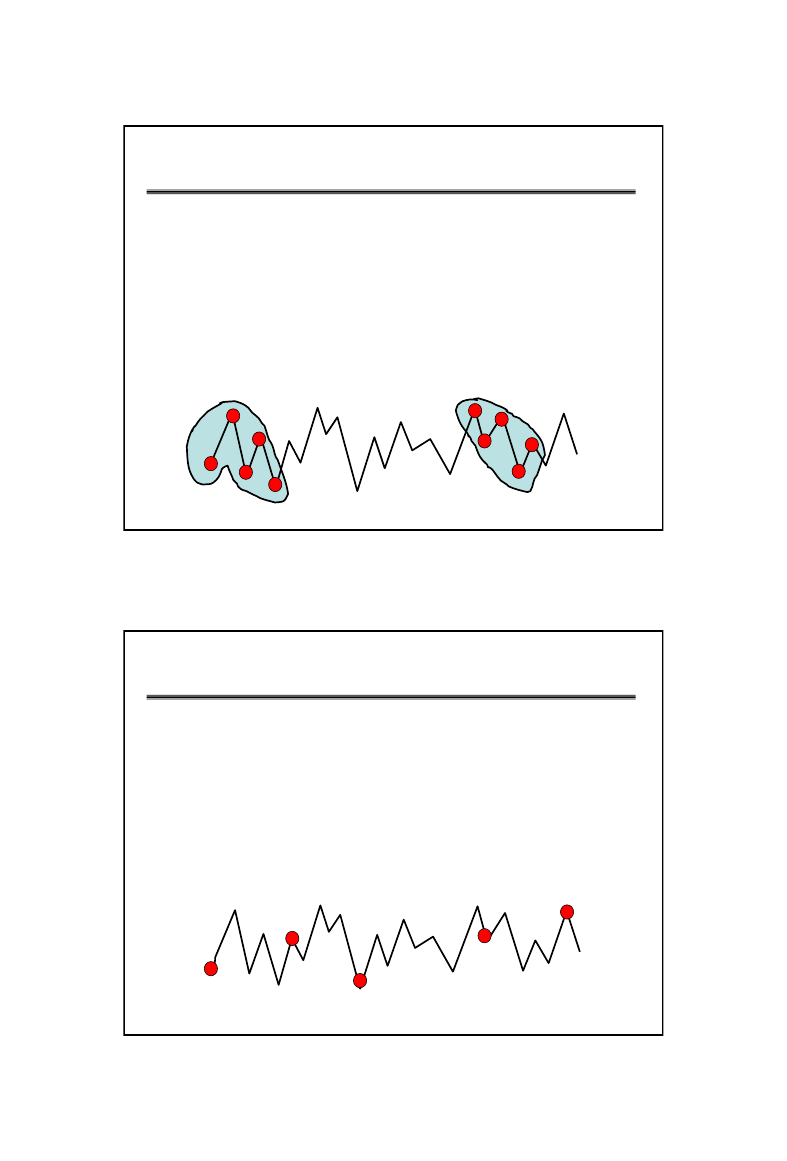
RACJONALNY ROZMIAR PRÓBKI

• Tworzenie próbki z kolejno

wychodzących po sobie jednostek
z procesu jest w takim przypadku
najbardziej logiczne

Próbki mają być tak pobierane,

aby zmienność w obrębie próbki

była w możliwie

jak największym stopniu

rezultatem tylko przyczyn losowych

14

A.Jednoróg – SPC

27

RACJONALNY ROZMIAR PRÓBKI

•

Dwa podejścia są możliwie:

1.

Każda próbka tworzona jest z kolejno
wychodzących po sobie jednostek
z procesu (wytworzonych możliwie w tym
samym czasie)

•

wtedy, gdy podstawowym celem karty kontrolnej
jest wykrycie zmian średniej procesu

Próbka 1

Próbka 2

A.Jednoróg – SPC

28

RACJONALNY ROZMIAR PRÓBKI

2.

Próbkę stanowią jednostki, które są
reprezentatywne dla wszystkich jednostek,

które zostały wyprodukowane od momentu

pobrania poprzedniej próbki

•

wtedy, gdy podstawowym celem karty kontrolnej
jest wspomaganie decyzji o akceptacji
wszystkich jednostek wyprodukowanych
w danym czasie

Próbka n=5

15

A.Jednoróg – SPC

29

GRANCIE KONTROLNE

• Odległość miedzy granicami kontrolnymi dla

karty X-

średnie zależy od wartości średniego

rozstępu (od zmienności

w próbce – WITHIN)

• Karta kontrolna odpowiada na pytanie:

– Czy zmienność między próbkami

(BETWEEN)

jest

większa niż zmienność w próbce

(WITHIN)

• To rozróżnienie wymaga odpowiedniego

pobierania próbek

A.Jednoróg – SPC

30

1.

W ten sposób minimalizowane jest są szanse pojawienia się zmienności specjalnych w

próbce, natomiast maksymalizowane są szanse pojawienia się zmian między próbkami, gdy w

procesie pojawią się przyczyny specjalne.

–

Ten sposób pobierania próbki daje lepsze oszacowania wartości odchylenia
standardowego procesu w przypadku kart kontrolnych dla danych liczbowych.

–

Każda próbka pobrana w ten sposób jest swego rodzaju „zdjęciem” procesu w momencie
jej pobierania.

2.

W przypadku, gdy w procesie występują zmiany średniej procesu między próbkami (tzw.

proces destabilizuje się i wraca do stanu stabilnego) będące wynikiem pojawienia się przyczyn

specjalnych, pierwsza metoda pobierania próbki wydaje się być nieskuteczną w wykrywaniu

takich zmian w procesie i drugi sposób pobierania próbki może być prefereowany.

–

Ale UWAGA!!!

–

Jeśli średnia procesu dryfuje, ulega zmianom, taki sposób pobierania próbek może

powodować, że rozproszenia w próbce będą bardzo duże, a konsekwencji granice

kontrolne bardzo szerokie. W ten sposób każdy proces, nawet ten statystycznie

niestabilny, można uczynić, ale tylko „na papierze” statystycznie stabilnym.

–

Taki sposób tworzenia próbki da w rezultacie mniejsze wartości wskaźników zdolności

procesu Cp i Cpk, jeżeli do ich obliczania zostanie użyta wartość odchylenia

standardowego szacowanego na podstawie rozstępów z próbki.

–

Taki sposób pobierania próbki może spowodować pojawienie się punktów poza granicami

kontrolnymi na kartach rozrzutu (R lub s) nawet wtedy, gdy w procesie nie pojawiły się

fałszywe alarmy.