Piotr Kucab Rzeszów, 18.03.2008 r.

I BD, LP6

POLITECHNIKA RZESZOWSKA WYDZIAŁ BUDOWNICTWA I INŻYNIERII ŚRODOWISKA KATEDRA FIZYKI

Laboratorium z fizyki

Ćw. 48 Wyznaczanie ogniskowej soczewki metoda Bessela

I. Zagadnienia do samodzielnego opracowania

1. Równanie dla cienkiej soczewki.

2. Konstruowanie obrazów za pomocą soczewek.

3. Definicja powiększenia obrazu.

II. Wprowadzenie:

Soczewki - równanie soczewki, powstawanie obrazu w soczewkach

Soczewką nazywamy ciało przezroczyste ograniczone dwiema powierzchniami kulistymi (wypukłymi lub wklęsłymi) lub jedną powierzchnią kulistą, a jedną płaską. Każda powierzchnia kulista soczewki ma swój środek krzywizny i odpowiadający jej promień (np.
i
). Prostą przechodzącą przez oba środki nazywa się osią główną soczewki. Promienie biegnące równolegle do osi głównej skupiają się po załamaniu w soczewce w punkcie zwanym ogniskiem soczewki (
i
). Każda soczewka ma dwa ogniska leżące po przeciwnych stronach soczewki. Odległość tego punktu do środka soczewki nosi nazwę ogniskowej soczewki (
lub
). Ogniskowe soczewek bardzo cienkich są sobie równe. Przy pomocy soczewek uzyskuje się odwzorowania przedmiotów. W celu wykreślenia obrazu przedmiotu otrzymywanego przy użyciu cienkiej soczewki, rysujemy dwa promienie:

a) promień przechodzący przez środek geometryczny soczewki, który nie ulega załamaniu,

b) promień równoległy do głównej osi soczewki, który po załamaniu w soczewce przechodzi przez ognisko.

Powiększenie liniowe obrazu definiujemy jako stosunek wysokości obrazu do wysokości przedmiotu, co daje:

Ogólne równanie soczewki:

=


gdzie: x - jest odległością przedmiotu od środka soczewki,

y - jest odległością obrazu od środka soczewki.

Z analizy równania soczewki wynika, że za pomocą soczewek możemy otrzymywać obrazy:

a) rzeczywiste: odwrócone, powiększone lub pomniejszone,

b) urojone: nieodwrócone, powiększone lub pomniejszone.

Można również wyprowadzić zależność między ogniskową f soczewki, a jej promieniami krzywizny
i
oraz współczynnikami załamania soczewki n i ośrodka otaczającego soczewkę n'

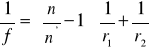
Zgodnie z tą zależnością ogniskowa soczewki zależy od współczynników załamania n i n', a więc zmienia się zdolność skupiająca soczewki. Gdy n '>n z soczewki skupiającej otrzymuje się rozpraszającą (f ujemne). Przekształcając równanie otrzymujemy wzór, przy pomocy, którego można wyliczyć ogniskową soczewki:

W tym celu wystarczy zmierzyć odległość przedmiotu od soczewki x i odległość obrazu od soczewki y.

Inną metodą pomiaru odległości ogniskowej soczewki jest metoda Bessela. Dla ustalonej odległości ekranu od przedmiotu (oznaczamy ją przez e) istnieją dwa różne położenia soczewki, przy których na ekranie otrzymuje się rzeczywisty obraz przedmiotu - jeden powiększony, drugi pomniejszony.

III. Wykonanie ćwiczenia

1. Ustawić układ pomiarowy jak na podanych rysunkach 2 i 3, odczytać ze skali odległość e między przedmiotem P a ekranem E.

2. Przesuwając soczewkę w kierunku ekranu znaleźć takie jej położenie y
, aby na ekranie widoczny był powiększony ostry obraz przedmiotu. Zmierzyć również wysokość powstałego obrazu
.

3. Przesuwając dalej soczewkę w kierunku ekranu przy niezmienionym e znaleźć drugie jej położenie y
takie, aby na ekranie powstał ostry pomniejszony obraz przedmiotu. Zmierzyć wysokość powstałego obrazu H
.

4. Czynności wymienione w punkcie 2 i 3 powtórzyć 10 razy.

IV. Tabela pomiarowa:

Lp.		a	b		Ha	Hb
	[cm]	[cm]	[cm]	[cm]	[mm]	[mm]	[cm]	[cm]
1.	85	54,5	29,5	25,0	11,0	4,0		0,65
2.			53,7	29,3	24,4	10,5			3,8
3.			54,2	29,6	24,6	11,2			3,9
4.			54,5	29,5	25,0	11,1			3,8
5.			54,7	29,9	24,8	11,1			3,7
6.			55,0	29,0	26,0	11,2			3,8
7.			55,2	29,8	25,4	11,4			3,9
8.			54,7	29,7	25,0	11,0			3,6
9.			54,4	29,7	24,7	10,9			3,7
10.			54,0	29,8	24,2	11,0			3,7

V. Błedy pomiarowe:

₌

₌

₌

₌

₌

₌

=
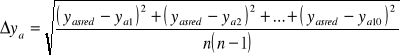
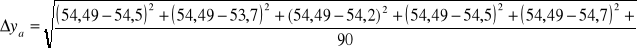
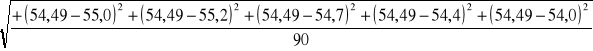
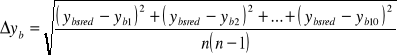
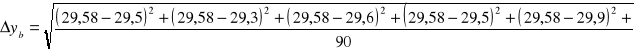
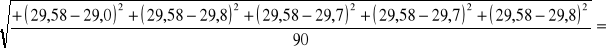
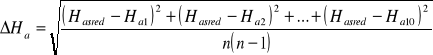
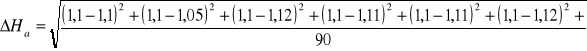
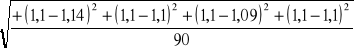
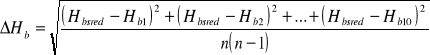
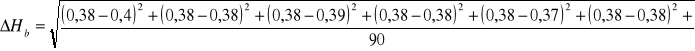
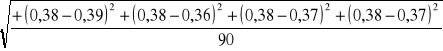
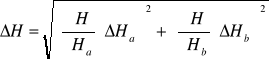
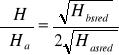
=0,29

=

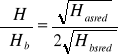
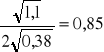
_{- błąd dokładności odczytu}

=

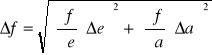
VI. Obliczenia :

a_śr=

n- ilość pomiarów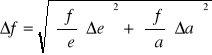







=




m=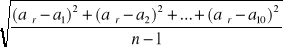

po podstawieniu: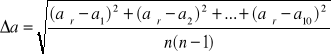



H=

liczymy H_aśr i H_bśr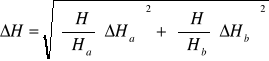

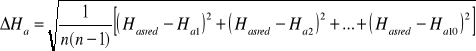
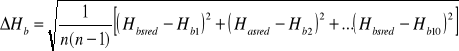
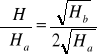
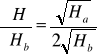
= 54,5 - 29,5 = 25,0 [cm]

= 53,7 - 24,4 = 24,4 [cm]

= 54,2 - 24,6 = 24,6 [cm]

= 54,5 - 29,5 = 25,0 [cm]

= 54,7 - 29,9 = 24,8 [cm]

= 55,0 - 29,0 = 26,0 [cm]

= 55,2 - 29,8 = 25,4 [cm]

= 54,7 - 29,7 = 25,0 [cm]

= 54,4 - 29,7 = 24,7 [cm]

= 54,0 - 29,8 = 24,2 [cm]

=

=


=

=

=

=

=

=

=

=

=

=









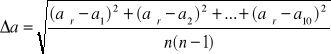
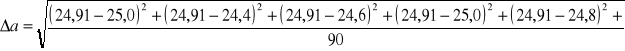
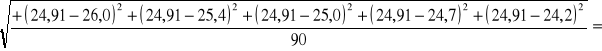
H=

H₁=

H₂=

H₃=

H₄=

H₅=

H₆=

H₇=

H₈=

H₉=

H₁₀=

H_śr=

VII. Wnioski:

Z przeprowadzonego doświadczenia wynika, że metoda Bessela daje dokładniejsze wyniki teoretycznie oraz praktycznie dowodzi to, iż jest ona jedną z najlepszych metod pomiarowych. Obliczony błąd nie jest dużej wielkości, ponieważ pomiar był przeprowadzony z precyzją i dokładnością oraz aparat pomiarowy spełnił podstawowe wymagania pracowni gdyż nie okazał się doszczętnie wyeksploatowany, co pomogło w dokładniejszym przeprowadzeniu ćwiczenia.

---