Politechnika
Częstochowska
Katedra Fizyki
ĆWICZENIE NR 14
TEMAT: Pomiar promienia krzywizny soczewki
płasko - wypukłej metodą pierścieni
Newtona.
Wydz. Elektryczny
Grupa dziekańska III
Piątek 8 - 10
Skład grupy:
Jasztal Mariusz
Osiecki Robert
1.OPIS TEORETYCZNY
Udowodniono, że światło można traktować zarówno jako zbiór cząstek (fotonów) wylatujących ze źródła światła i poruszających się po liniach prostych (korpuskularna teoria światła wyjaśniająca np. bardzo dobrze zjawisko fotoelektryczne czy efekt Comptona), jak też jako falę z wszystkimi charakterystycznymi dla niej własnościami (np. dyfrakcja, interferencja, polaryzacja).
W tym drugim ujęciu światło jest falą elektromagnetyczną, poprzeczną, rozchodzącą się przestrzeni z bardzo dużą predkością. Do najbardziej spektakularnych zjawisk falowych należą zjawiska związane z interferencją fal świetlnych.
Aby nastąpiła interferencja muszą się spotkać co najmniej dwa ciągi falowe, które są ze sobą spójne.
Do niedawna (zanim nie wymyślono laserów), uzyskanie dwóch spójnych wiązek światła nie było proste. Aby to wyjaśnić należy przypomnieć jaki jest mechanizm powstawania światła.
Otóż elektrony w atomach i cząsteczkach posiadają pewną energię (potencjalną i kinetyczną) związaną z oddziaływaniem z jądrami atomów. Energia ta nie jest dowolna , lecz może przybierać tylko pewne określone wartości (mówimy, że energie elektronów są skwantowane). Elektron może zmienić swą energię tylko wtedy, gdy oddaje do otoczenia (lub pobiera z otoczenia) ściśle określoną porcję energii. Mówimy, że gdy elektron spada z wyższej orbity na niższą (bliższą jądra) to oddaje energię, a gdy przechodzi na orbitę wyższą, musi pobrać energię. Porcja oddawanej lub pobieranej energii musi być dokładnie równa różnicy energii energii dozwolonych dla tego elektronu orbit.
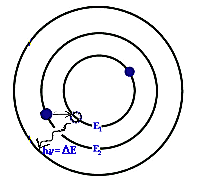
Innymi słowy, tak jak to widać na rysunku obok, elektron przeskakuje z jednego poziomu energetycznego dozwolonego (na którym ma energię E2) na inny, niższy (o energii E1), oddając porcję energii odpowiada dokładnie różnicy E = E2 - E1 między dozwolonymi poziomami energetycznymi elektronu.
![]()
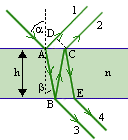
W ten sposób powstaje światło. Lecz światło z klasycznych źródeł światła nigdy nie jest spójne. Po pierwsze dla tego, że większość źródeł nie daje światła monochromatycznego (o jednej długości fali), lecz określone widmo (bardzo często ciągłe, jak np. żarówka). Po drugie, nawet światło ze źródła monochromatycznego, jak np. używana w tym ćwiczeniu lampa sodowa nie daje światła spójnego. Otóż wiązka światła składa się z fal pochodzących z bardzo wielu promieniujących atomów ciała świecącego. Są one spolaryzowane w zupełnie przypadkowy sposób, a pnadto nakładają się wszystkie na siebie w zupełnie przypadkowych fazach. Aby więc można było zaobserwować interferencję, należy z takiej wiązki wydzielić te fale, które są spójne. Jedną z metod jest rozdzielenie jednej fali na dwie wiązki, a następnie doprowadzenie do ich nałożenia się w odpowiednich fazach. Efekt ten uzyskuje się na przykład w przypadku interferencji światła w cienkich warstwach. "Cienkich" oznacz tu" taką grubość, przy której nie jest przekroczony tzw. zakres spójności fal interferujących, to znaczy, mówiąc w skrócie, aby fala po przejściu owej "cienkiej warstwy" zdążyła jeszcze spotkać się z tą samą wiązką,od której została oddzielona. Zasadę interferencji w cienkiej warstwie omówię w oparciu o rysunek:
![]()
Promień monochromatycznego światła padający na płytkę w punkcie A ulega częściowo odbiciu (i biegnie dalej jako promień 1), a częściowo załamaniu. Promień załamany ulega kolejnym odbiciom i załamaniom w punktach B,C i E W rezultacie możemy uzyskać po dwa promienie po każdej stronie płytki. Jeżeli warstwa jest dostatecznie cienka (dla światła widzialnego powinna być rzędu ułamka milimetra), promienie 1 i 2 oraz 3 i 4 mogą ze sobą interferować.
Korzystając z prawa załamania i z prawa odbicia
można wyprowadzić wzór określający warunki, przy których w świetle odbitym powstają ciemne prążki (interferencyjne osłabienie):
![]()
lub wzór opisujący powstawanie jasnych prążków:
Jak widać, wynik interferencji zależy zarówno od kąta padania jak i od grubości warstwy.
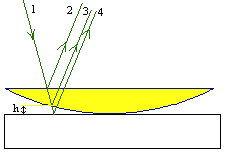
Powstające prążki interferencyjne nazywamy prążkami jednakowej grubości, gdyż odpowiadają ściśle określonej grubości h które dalej będzie równe dk warstwy ośrodka. Jeszcze lepiej wyjaśnimy tę nazwę omawiając powstawanie pierścieni Newtona. Rolę cienkiej warstwy pełni warstwa powietrza między soczewką a płytką szklaną :
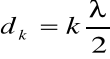
Interferować mogą tylko promienie 3 i 4, gdyż grubość soczewki jest zbyt duża, aby pozostałe promienie były spójne.
Wybierzmy np. prążki ciemne (otrzymamy nieco krótszy wzór) i zastosujmy podaną wyżej zależność przyjmując jako wartość współczynnika załamania n=1 (cienką warstwą jest tu powietrze) oraz sinus równy 0 (promienie padają na soczewkę pionowo z góry, czyli kąt padania jest równy zero). Otrzymamy więc wzór:
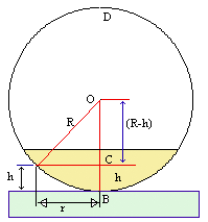
Z drugiej strony, z warunków geometrycznych przedstawionych na rysunku:
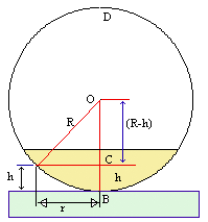
otrzymujemy:
(R-dk)2 + r2 = R2
![]()
Z trójkąta DCE znajdziemy, że
czyli:
r2 = 2 dk R - dk 2
Gdzie R jest promieniem krzywizny powierzchni I
a ponieważ warstwa jest bardzo cienka,a promień soczewki bardzo duży możemy pominąć dk2 (gdyż dk<<rk można przyjąć)jako bardzo małe.
Tak więc mamy dwa wzory:
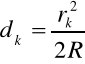
r2 = 2 d k R
d k = 1/2 k
z których otrzymujemy:
r2 = k R
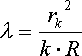
i ostatecznie:
Ze wzoru tego wynika, że znając długość fali światła oświetlającego układ, przez pomiar k- tego prążka można znaleźć promień krzywizny soczewki lub na odwrót. Aby uniknąć błędu spowodowanego niedokładnym oznaczeniem środka pierścienia ciemnego mierzymy średnice dwóch ciemnych pierścieni ( możliwie daleko odległych od siebie ) np. m- tego i n- tego.
![]()
![]()
Wówczas
![]()
Odejmując stronami te równania otrzymamy:
2. Układ pomiarowy
W celu wykonania ćwiczenia posługujemy się mikroskopem i układem płytek. Światło z lampy sodowej jest skupiane za pomocą soczewki. Po odbiciu od zwierciadła (wewnątrz mikroskopu) pada na układ płytek, dających wskutek odbicia i interferencji pierścienie Newtona. Promienie odbite trafiają do obiektywu mikroskopu, a następnie do oka obserwatora. W okularze mikroskopu znajduje się nić pajęcza, którą możemy przesuwać za pomocą śrub mikrometrycznych.
3. Tabela pomiarowa
nr pierścienia K |
Wskazania mikrometru
|
r k= [m] |
m , n
|
λ [m] |
R [m] |
Rśr [m] |
||
|
na lewo l [m] |
na prawo p [m] |
|
|
|
|
|
|
6 |
29.84 ⋅10-3 |
21.85 ⋅10-3 |
3.99 ⋅10-3 |
35,15 |
5.89 ⋅10-7 |
4.24 |
4.28 |
|
7 |
30.13 ⋅10-3 |
21.56 ⋅10-3 |
4.28 ⋅10-3 |
20,7 |
5.89 ⋅10-7 |
4.28 |
|
|
8 |
30.43 ⋅10-3 |
21.26 ⋅10-3 |
4.58 ⋅10-3 |
30,9 |
5.89 ⋅10-7 |
4.28 |
|
|
9 |
30.68 ⋅10-3 |
21.00 ⋅10-3 |
4.84 ⋅10-3 |
20,6 |
5.89 ⋅10-7 |
4.27 |
|
|
10 |
30.90 ⋅10-3 |
20.75 ⋅10-3 |
5.07 ⋅10-3 |
25,15 |
5.89 ⋅10-7 |
4.30 |
|
|
11 |
31.93 ⋅10-3 |
19.57 ⋅10-3 |
6.18 ⋅10-3 |
30,25 |
5.89 ⋅10-7 |
4.35 |
|
|
12 |
32.90 ⋅10-3 |
18.60 ⋅10-3 |
7.15 ⋅10-3 |
25,9 |
5.89 ⋅10-7 |
4.25 |
|
|
13 |
33.75 ⋅10-3 |
17.80 ⋅10-3 |
7.97 ⋅10-3 |
30,20 |
5.89 ⋅10-7 |
4.29 |
|
|
14 |
34.51 ⋅10-3 |
17.03 ⋅10-3 |
8.74 ⋅10-3 |
35,10 |
5.89 ⋅10-7 |
4.24 |
|
|
15 |
35.16 ⋅10-3 |
16.37 ⋅10-3 |
9.39 ⋅10-3 |
25,10 |
5.89 ⋅10-7 |
4.28 |
|
|
16 |
35.64 ⋅10-3 |
15.72 ⋅10-3 |
9.96 ⋅10-3 |
|
|
|||
17 |
36.13 ⋅10-3 |
15.16 ⋅10-3 |
10.4 ⋅⋅10-3 |
|
|
|||
4. Przykładowe obliczenia
a) promień pierścienia
[m]
b) promień soczewki R
dla m=35, n=15
[m]
c) wyznaczanie średniej wartości promienia
[m]
5. Rachunek błędów i wyników
a) błędy Δrm i Δrn zależące od dokładności nastawienia środka krzyża nici pajęczej w
stosunku do prążka interferencyjnego.
Błąd ten oszacowujemy doświadczalnie przez trzykrotne ustawienie środka krzyża na
środku prążka, odczytanie wskazania mikrometru, obliczenie średniego wskazania.
Maksymalne odstępstwo od średniej przyjmujemy jako (Δl)=(Δp).
(Δrm)=(Δrn)=2 ⋅(Δl)
Pomiary:
[m]
[m]
[m]
Obliczamy wartość średnią:
[m]
(Δl)=(Δp)= [m]
(Δrm)=(Δrn)=2(Δl)= [m]
b) błąd średni kwadratowy:
[m]
ε1 = R1 - Rsr = 4.24 - 4.28 = -0.04 [m]
ε2 = R2 - Rsr = 4.28 - 4.28 = 0 [m]
ε3 = R3 - Rsr = 4.28 - 4.28 = 0 [m]
ε4 = R4 - Rsr = 4.27 - 4.28 = -0.01 [m]
ε5 = R5 - Rsr = 4.30 - 4.28 = 0.02 [m]
ε6 = R6 - Rsr = 4.35 - 4.28 = 0.07 [m]
ε7 = R7 - Rsr = 4.25 - 4.28 = -0.03 [m]
ε8 = R8 - Rsr = 4.29 - 4.28 = 0.01 [m]
ε9 = R9 - Rsr = 4.24 - 4.28 = -0.04 [m]
ε10 = R10 - Rsr = 4.28 - 4.28 = 0 [m]
ΔR = 0.033 [m]
![]()
![]()
[m]
6.Wnioski nad błędami
Niedokładność pomiarów oraz błędy jakie w czasie tych pomiarów otrzymałem uzależnione są od:
- niedokładności urządzeń pomiarowych - w naszym przypadku mikroskopu
- niedokładności odczytów
- zaokrągleń liczb w czasie wykonywania obliczeń
![]()
d k
R - d k
![]()
![]()
![]()
![]()
![]()
(R-d k)
Wyszukiwarka
Podobne podstrony:
Opt- Pomiar promienia krzywizny soczewki płasko - wypukłej m, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko wypukłej metod DOC
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko - wypukłej(1), Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko - wypukłej metodą pierścieni Newtona, Sprawozdania - Fizyk
Pomiar promieni krzywizny soczewki płasko-wypukłej 2, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko-wypukłej metodą pierścieni Newtona, POLITECHNIKA CZ˙STOCHO
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki plasko- w p, Sprawozdania - Fizyka
Wyznaczania promieni krzywizny soczewki płasko-wypukłej meto, Akademia Morska Szczecin Nawigacja, uc
Wyznaczania promienia krzywizny soczewki płasko-wypukłej2, Fizyka
OP Pomiar promieniowania krzywizny soczewki, Wiadomo˙ci teoretyczne
72a promień krzywizny soczewek, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Lab
promień krzywizny soczewek, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolat
Opt- Pomiar stałej Siatki Dyfrakcyjnej za Pomocą Spektrometr, Sprawozdania - Fizyka
sprawka fizyka, Wyznaczanie promienia krzywizny soczewki za pomocą pierścieni Newtona
Lab26, Wyznaczanie promienia krzywizny soczewki za pomoc? pier?cieni Newtona
Wyznaczanie ogniskowych soczewek i pomiar powierzchni krzywizny soczewek 2, MARCIN SOWIK
więcej podobnych podstron