Politechnika Wrocławska Wrocław 6.06.2009
Wydział Budownictwa Lądowego i Wodnego
Zakład Budownictwa Ogólnego
Ćwiczenie projektowe nr 2
Obliczenie elementów stropu.
Obliczenie nadproża.
Wykonał:
Marcin Leśniewski
Spis treści
Strona tytułowa............................................................................................... 1
Spis treści........................................................................................................ 2
Obliczenie belki stropowej. Pozycja obliczeniowa (II.1).......................... 3
Dane przyjęte do obliczeń........................................................................ 3
Obciążenie .............................................................................................. 3
Sprawdzenie konieczności obliczenia zbrojenia na ścinanie oraz
szerokości rozwarcia rys......................................................................... 6
Sprawdzenie szerokości rys prostopadłych............................................... 7
Sprawdzenie ugięcia............................................................................... 7
Obliczenie belki stropowej. Pozycja obliczeniowa (II.2).......................... 8
Dane przyjęte do obliczeń........................................................................ 8
Obciążenie .............................................................................................. 3
Sprawdzenie konieczności obliczenia zbrojenia na ścinanie oraz
szerokości rozwarcia rys......................................................................... 10
Sprawdzenie szerokości rys prostopadłych.............................................. 11
Sprawdzenie ugięcia............................................................................... 12
Obliczenie nadproża drzwiowego. Pozycja obliczeniowa (III.1)............. 12
Dane przyjęte do obliczeń ....................................................................... 12
Obliczenie nośności nadproża ................................................................. 13
Podwójne żebro stropu Akermana o rozpiętości 6,00m. Pozycja obliczeniowa 1.
Dane przyjęte do obliczeń
- strop Akermana
- rozpiętość stropu w świetle ![]()
- rozstaw żeber ![]()
- wysokość pustaka ![]()
- grubość płyty nadbetonu ![]()
- strop swobodnie podparty, współczynnik ![]()
- beton klasy B25 o: ![]()
;![]()
;![]()
;![]()
; ![]()
- warunki środowiskowe suche, wnętrze budynku o niskiej wilgotności powietrza - klasa XC1
- stal klasy A-III o znaku gatunku 34 GS i ![]()
oraz ![]()
Obciążenia
Obciążenie |
Obciążenie charakterystyczna [kN/m2] |
Współczynnik obciążenia |
Wartość obliczeniowa [kN/m2] |
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
panele podłogowe laminowane grubości 8mm
|
0,1 |
|
1,2 |
0,12 |
pianka pod panele 3mm
|
0,07 |
|
1,2 |
0,084 |
gładź cementowa 35 mm
|
0,735 |
|
1,3 |
0,956 |
folia PE 0,2mm |
- |
|
- |
- |
styropian EPS T 20mm
|
0,01 |
|
1,2 |
0,012 |
strop Akermana 3,12 |
3,12 |
|
1,1 |
3,432 |
tynk cementowy 10mm
|
0,19 |
|
1,3 |
0,247 |
RAZEM |
4,225 |
|
|
4,851 |
gp. obciążenie stałe z prawej strony |
|
|
|
|
panele podłogowe laminowane grubości 8mm
|
0,1 |
|
1,2 |
0,12 |
pianka pod panele 3mm
|
0,07 |
|
1,2 |
0,084 |
gładź cementowa 35 mm
|
0,735 |
|
1,3 |
0,956 |
folia PE 0,2mm |
- |
|
- |
- |
styropian EPS T 20mm
|
0,01 |
|
1,2 |
0,012 |
płyta monolityczna
|
3,0 |
|
1,3 |
3,9 |
wełna mineralna
|
0,28 |
|
1,2 |
0,336 |
tynk cementowy 10mm
|
0,19 |
|
1,3 |
0,247 |
RAZEM |
4,385 |
|
|
5,655 |
p - obciążenie zmienne technologiczne |
|
|
|
|
1.5 |
1,5 |
|
1,4 |
2,1 |
obciążenie zastępcze od ścianek działowych 0,25 |
0,25 |
|
1,2 |
0,3 |
RAZEM gl + p |
5,975 |
|
|
7,251 |
RAZEM gp + p |
6,135 |
|
|
8,055 |
Wartość obliczeniowa obciążenia przypadająca na żebro stropu wynosi:
![]()
Rozpiętość obliczeniowa żebra stropu wynosi:
![]()
Schemat statyczny żebra.
1)powyżej stropu i pod stropem wymurowana jest ściana, a średnie naprężenie obliczeniowe jej muru ![]()
2)strop jest oparty na ścianie za pośrednictwem wieńca żelbetowego a szerokość ![]()
równej grubości ściany ![]()
i nie mniejszej od wysokości konstrukcji stropu ![]()
, atak by zapewnione było odpowiednie ramię pary sił mocujących.
3)w końcówce żebra wypuszczone są pręty zbrojenia górnego (o przekroju wystarczającym do przeniesienia momentu utwierdzenia ) zaopatrzone w haki wchodzące w wieniec (przy użyciu stali żebrowanej haków nie stosuje się).
![]()
L |
1 |
2 |
3 |
P |
1 |
2 |
3 |
|
nie |
tak |
tak |
|
nie |
nie |
tak |
Moment zginający żebra wynosi:
![]()
Przyjęto grubość otulenia zbrojenia betonu c= 15mm, strzemiona średnicy 6 mm, pręty zbrojeniowe żeber średnicy 14mm i dopuszczalną odchyłkę otuliny ![]()
.Przy tych założeniach wysokość użyteczna przekroju wynosi:
![]()
Strefa ściskana wynosi:
![]()
A moment zginający przenoszony przez przekrój ![]()
wynosi:
![]()
![]()
Przekrój jest pozornie teowy.
Wartość współczynnika 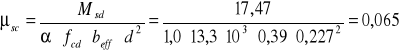
Dla wartości ![]()
odczytano ρ = 0, 25% i obliczono pole przekroju zbrojenia:
![]()
Dla obliczonego pola przekroju przyjęto pręty średnicy 16 mm, o polu przekroju:
![]()
Sprawdzenie warunku na minimalne pole przekroju zbrojenia rozciąganego:
![]()
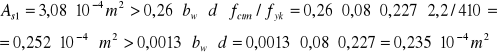
.
Warunek jest spełniony.
Sprawdzenie konieczności obliczenia zbrojenia na ścianie oraz szerokości rozwarcia rys.
Wartość siły poprzecznej wynosi:
-w licu podpory ![]()
- w odległości d od podpory ![]()
Najmniejsza szerokość strefy ścinania ![]()
.
Współczynnik ![]()
,![]()
Stopień zbrojenia: ![]()
przyjęto ![]()
Siła ![]()
wynosi:
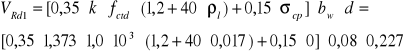
![]()
Siła ![]()
na odcinkach pierwszego rodzaju wynosi:
![]()
![]()
![]()
![]()
Zbrojenie na ścinanie i szerokość rozwarcia rys ukośnych nie są obliczane, ponieważ: ![]()
Sprawdzenie szerokości rys prostopadłych.
Dla środowiska klasy 1 ![]()
. Ponieważ strop projektowany jest w budynku mieszkalnym, to ![]()
.
Wartość charakterystyczna obciążenia żebra w kombinacji obciążeń długotrwałych wynosi:
![]()
![]()
Moment zginający dla kombinacji obciążeń długotrwałych wynosi:
![]()
Naprężenia ![]()
w zbrojeniu rozciąganym wynoszą:
![]()
więc: ![]()
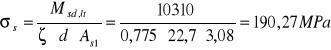
Spełniony jest warunek:
![]()
Dla przyjętego zbrojenia ![]()
i ![]()
można stosować pręty średnicy do 32mm. Ponieważ przyjęto pręty średnicy 14 mm, to bez szczegółowych obliczeń można stwierdzić, że dopuszczalna szerokość rozwarcia rys nie będzie przekroczona.
Sprawdzenie ugięcia.
Ponieważ ![]()
![]()
![]()
![]()
![]()
![]()
więc: ![]()
W omawianym przykładzie:
![]()
Normy PN-B-03264:2002 (tab. 13) nie przewiduje ![]()
, dla betonu klasy B25.
Dlatego należy wykonać ugięcie doświadczalnie w laboratorium wytrzymałościowym, a następnie określić czy jest ono dopuszczalne: ![]()
. W przypadku gdy nie zostanie spełniony warunek należy wykorzystać jedno z rozwiązań producenta na zredukowanie ugięcia.
Podwójne żebro stropu Akermana o rozpiętości 6,00m. Pozycja obliczeniowa 2.
Dane przyjęte do obliczeń
- strop Akermana
- rozpiętość stropu w świetle ![]()
- rozstaw żeber ![]()
- wysokość pustaka ![]()
- grubość płyty nadbetonu ![]()
- strop swobodnie podparty, współczynnik ![]()
- beton klasy B25 o: ![]()
;![]()
;![]()
;![]()
; ![]()
- warunki środowiskowe suche, wnętrze budynku o niskiej wilgotności powietrza - klasa XC1
- stal klasy A-III o znaku gatunku 34 GS i ![]()
oraz ![]()
Obciążenia
Obciążenie |
Wartość charakterystyczna [kN/m2] |
Współczynnik obciążenia |
Wartość obliczeniowa [kN/m2] |
1 |
2 |
3 |
4 |
g. obciążenie stałe |
|
|
|
panele podłogowe laminowane grubości 8mm
|
0,1 |
1,2 |
0,12 |
pianka pod panele 3mm
|
0,07 |
1,2 |
0,084 |
gładź cementowa 35 mm
|
0,735 |
1,3 |
0,956 |
folia PE 0,2mm |
- |
- |
- |
styropian EPS T 20mm
|
0,01 |
1,2 |
0,012 |
strop Akermana 3,12 |
3,12 |
1,1 |
3,432 |
tynk cementowy 10mm
|
0,19 |
1,3 |
0,247 |
RAZEM |
4,225 |
|
4,851 |
p - obciążenie zmienne technologiczne |
|
|
|
1.5 |
1,5 |
1,4 |
2,1 |
obciążenie zastępcze od ścianek działowych 0,25 |
0,25 |
1,2 |
0,3 |
RAZEM g + p |
5,975 |
|
7,251 |
ściana działowa początek
|
0,744 |
1,1 |
0,818 |
ściana działowa koniec
|
4,018 |
1.1 |
4,419 |
Wartość obliczeniowa obciążenia przypadająca na żebro stropu wynosi:
![]()
oraz obciążenie od ścianki działowej na długości 2,2m o zmiennej wysokości.
Wartość obciążenia zmienia się liniowo:
z wartości ![]()
do wartości ![]()
.
Rozpiętość obliczeniowa żebra stropu wynosi:
![]()
Schemat statyczny żebra.
1)powyżej stropu i pod stropem wymurowana jest ściana, a średnie naprężenie obliczeniowe jej muru ![]()
2)strop jest oparty na ścianie za pośrednictwem wieńca żelbetowego a szerokość ![]()
równej grubości ściany ![]()
i nie mniejszej od wysokości konstrukcji stropu ![]()
, atak by zapewnione było odpowiednie ramię pary sił mocujących.
3)w końcówce żebra wypuszczone są pręty zbrojenia górnego (o przekroju wystarczającym do przeniesienia momentu utwierdzenia ) zaopatrzone w haki wchodzące w wieniec (przy użyciu stali żebrowanej haków nie stosuje się).
![]()
L |
1 |
2 |
3 |
P |
1 |
2 |
3 |
|
nie |
tak |
tak |
|
nie |
nie |
tak |
Schemat obciążenia:
Wykres momentów:
Maksymalny moment zginający żebra wynosi:
![]()
Przyjęto grubość otulenia zbrojenia betonu c= 15mm, strzemiona średnicy 6 mm, pręty zbrojeniowe żeber średnicy 12 mm i dopuszczalną odchyłkę otuliny ![]()
.Przy tych założeniach wysokość użyteczna przekroju wynosi:
![]()
Strefa ściskana wynosi:
![]()
A moment zginający przenoszony przez przekrój ![]()
wynosi:
![]()
![]()
Przekrój jest pozornie teowy.
Wartość współczynnika 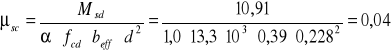
Dla wartości ![]()
odczytano ρ = 0, 15% i obliczono pole przekroju zbrojenia:
![]()
Dla obliczonego pola przekroju przyjęto pręty średnicy 12 mm, o polu przekroju:
![]()
Sprawdzenie warunku na minimalne pole przekroju zbrojenia rozciąganego:
![]()
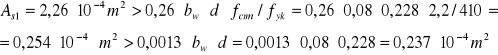
.
Warunek jest spełniony.
Sprawdzenie konieczności obliczenia zbrojenia na ścianie oraz szerokości rozwarcia rys.
Wartość siły poprzecznej wynosi:
-w licu podpory ![]()
- w odległości d od podpory ![]()
Najmniejsza szerokość strefy ścinania ![]()
.
Współczynnik ![]()
,![]()
Stopień zbrojenia: ![]()
przyjęto ![]()
Siła ![]()
wynosi:
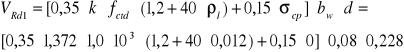
![]()
Siła ![]()
na odcinkach pierwszego rodzaju wynosi:
![]()
![]()
![]()
![]()
Zbrojenie na ścinanie i szerokość rozwarcia rys ukośnych nie są obliczane, ponieważ: ![]()
Sprawdzenie szerokości rys prostopadłych.
Dla środowiska klasy 1 ![]()
. Ponieważ strop projektowany jest w budynku mieszkalnym, to ![]()
.
Wartość charakterystyczna obciążenia żebra w kombinacji obciążeń długotrwałych wynosi:
![]()
![]()
oraz obciążenie od ścianki działowej na długości 2,2m o zmiennej wysokości.
Wartość obciążenia zmienia się liniowo:
z wartości ![]()
do wartości ![]()
.
Schemat obciążenia:
Wykres momentów:
Moment zginający dla kombinacji obciążeń długotrwałych wynosi:
![]()
Naprężenia ![]()
w zbrojeniu rozciąganym wynoszą:
![]()
więc: ![]()
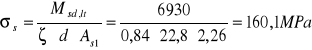
Spełniony jest warunek:
![]()
Dla przyjętego zbrojenia ![]()
i ![]()
można stosować pręty średnicy do 32mm. Ponieważ przyjęto pręty średnicy 12 mm, to bez szczegółowych obliczeń można stwierdzić, że dopuszczalna szerokość rozwarcia rys nie będzie przekroczona.
Sprawdzenie ugięcia.
Ponieważ ![]()
![]()
![]()
![]()
![]()
![]()
więc: ![]()
W omawianym przykładzie:
![]()
Z normy PN-B-03264:2002 (tab. 13) odczytano dla ![]()
, betonu klasy B25 i naprężeń ![]()
maksymalne które wynosi 19.
Uwzględniając obliczoną wartość naprężeń ![]()
, obliczono wartość :
![]()
Ponieważ wartość ta jest większa od wartości obliczonej ugięcie stropu nie przekroczy wartości granicznej.
Obliczenie nadproża drzwiowego.
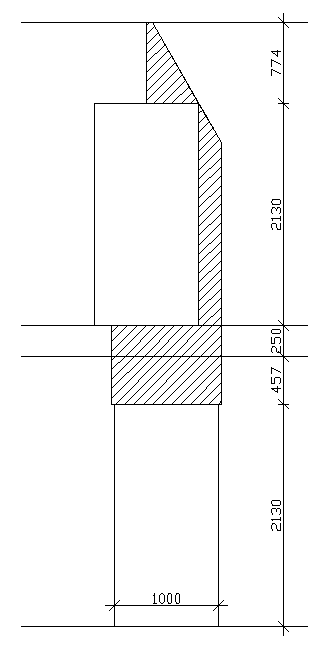
Otwór drzwiowy w świetle ścian ![]()
Ściana wykonana jest z sylikatu o grubości 25cm. Na ścianie, w której znajduje się projektowane nadproże, opiera się strop gęstożebrowy Akermana o rozpiętości ![]()
oraz płyta monolityczna o szerokości 42cm. Obciążenie dla stropu przyjęto 3,12 kN/m2. Przyjęto wstępnie dwie belki nadproża typu L-19.
Na podstawie rysunku określono powierzchnię muru, z której przypada obciążenie na rozpatrywane nadproże. Wynosi ![]()
Rozpiętość obliczeniowa nadproża wynosi:
![]()
Obciążenie dla stropu wynosi 7,251 kN/m2 a obciążenie od płyty 8,055 kN/m2 .
Obciążenie od stropu i płyty monolitycznej na nadproże wynosi:
![]()
,
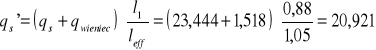
Obciążenie |
Wartość charakterystyczna [kN/m] |
Współczynnik obciążenia |
Wartość obliczeniowa [kN/m] |
1 |
2 |
3 |
4 |
g. obciążenie stałe |
|
|
|
mur z sylikatu 250 mm
|
4,66 |
1,1 |
5,13 |
tynk cementowo wapienny x 2 po 15mm
|
0,57 |
1,3 |
0,741 |
RAZEM |
5,23 |
|
5,867 |
wieniec żelbetowy
|
1,38 |
1,1 |
1,518 |
dwie belki nadprożowe L-19
|
1,20 |
1,1 |
1,32 |
obciążenie obliczeniowe od ciężaru muru wynosi:
![]()
Maksymalny moment obliczeniowy wynosi:
obciążenie obliczeniowe od ciężaru muru wynosi:
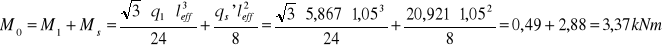
Wstępnie przyjęto dwie belki D/120. Posiadają one zbrojenie w postaci 2 prętów o średnicy 6 mm, o polu przekroju ![]()
![]()
klasa betonu B20 dla którego ![]()
Grubość otulenia przyjęto c= 15mm, strzemiona o średnicy 4,5mm, pręty zbrojenia żeber o średnicy 10mm i dopuszczalną odchyłkę otuliny h= 5mm. Przy tych założeniach wysokość użyteczna wynosi:
![]()
Stopień zbrojenia wynosi:
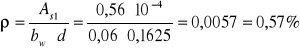
![]()
Nośność pojedynczej belki wynosi:
![]()
Ponieważ przyjęto dwie belki sumaryczna nośność wynosi:
![]()
Stan graniczny dla przyjętego nadproża jest spełniony.
Ostatecznie przyjęto dwie belki nadproża D/120
4