RÓWNOWAGI FAZOWE W UKŁADACH DWUSKŁADNIKOWYCH ; OPIS TERMODYNAMICZNY ROZTWORÓW

Zastosujmy regułę faz Gibbsa do układu dwuskładnikowego.

Wobec tego, jeśli w układzie jest jedna faza, to :

co oznacza, że można zmieniać niezależnie od siebie trzy parametry. Chcąc przedstawić zależności pomiędzy nimi trzeba by używać wykresów przestrzennych. Dlatego też przedstawiając równowagi w układach dwuskładnikowych ustala się jeden z parametrów (ciśnienie lub temperaturę), co redukuje liczbę zmiennych i pozwala przedstawić równowagi na płaszczyźnie. Maksymalna liczba faz, jakie mogą współistnieć w równowadze w układzie dwuskładnikowym to cztery; zmienność układu wynosi wówczas zero. Są to jednak bardzo specyficzne przypadki.

Będziemy rozpatrywać następujące równowagi :

• Ciecz - para

• Dwie ciecze z ograniczoną mieszalnością

• Ciecz - ciało stałe

Równowagi pomiędzy cieczą a parą w układzie dwuskładnikowym

Będziemy tu rozpatrywać dwa skrajne przypadki : jeden, gdy oba składniki w stanie ciekłym mieszają się w sposób nieograniczony, tworząc roztwory w całym zakresie stężeń oraz drugi, gdy oba składniki w stanie ciekłym nie mieszają się w ogóle, czyli tworzą dwie odrębne fazy ciekłe.

Roztwór doskonały

oznacza potencjał chemiczny czystego składnika ciekłego pod dowolnym ciśnieniem i w dowolnej temperaturze. Nazywamy go potencjałem chemicznym standardowym. Stanem standardowym dla składnika w roztworze doskonałym jest stan czystego, ciekłego składnika pod dowolnym ciśnieniem i w dowolnej temperaturze. Potencjał chemiczny standardowy przy tak przyjętym stanie standardowym zależy od temperatury i ciśnienia. Definiując roztwór doskonały dokonaliśmy wyboru stanu standardowego dla niego i zdefiniowaliśmy równocześnie potencjał chemiczny standardowy.

Z definicji roztworu doskonałego można wyprowadzić prawo Raoulta opisujące prężność par składnika nad roztworem.

Prawo Raoulta

Weźmy pod uwagę ciekły roztwór dwuskładnikowy zachowujący się w sposób doskonały. Prężność par każdego ze składników nad roztworem zgodnie z prawem Raoulta można wyrazić jako :

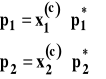
Całkowita prężność par nad roztworem jest sumą prężności obu składników zgodnie z prawem Daltona.

Ponieważ :

to całkowitą prężność par nad roztworem możemy wyrazić jako :

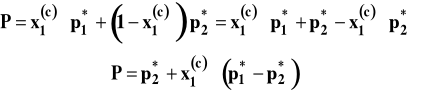
Jak widzimy, prężność całkowita nad roztworem jest liniową funkcją składu roztworu. Na rysunku 1 przedstawiono prawo Raoulta w postaci graficznej. Jak widać, prężności par obu składników są wprost proporcjonalne do ich ułamków molowych w cieczy, a prężność całkowita jest liniową funkcją składu roztworu.

Skład pary nad roztworem możemy wyrazić w oparciu o prawo Daltona. Dla ułamków molowych składnika w parze rezerwujemy symbol y.

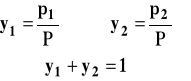
Rysunek 1. Graficzna ilustracja prawa Raoulta.

Uwzględniając otrzymane wcześniej wyrażenia opisujące prężności w funkcji składu cieczy, możemy skład pary opisać następująco :

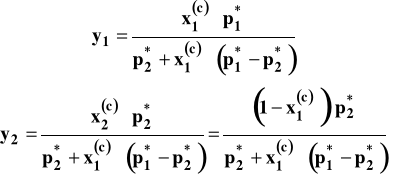
Można też po pewnych przekształceniach, które pominiemy, przedstawić prężność całkowitą nad roztworem w funkcji składu pary czyli ułamka molowego składnika 1 w parze y₁.

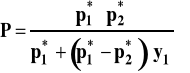
Jak widać, nie jest to zależność liniowa, a hiperboliczna. Jeśli wykreślimy na jednym rysunku zależność prężności całkowitej od składu cieczy (linia cieczy) i od składu pary (linia pary), to otrzymamy diagram fazowy dla równowagi ciecz -para w układzie dwuskładnikowym przy stałej temperaturze. Diagram taki ilustruje destylację izotermiczną. W obszarze zamkniętym linią cieczy i linią pary współistnieją w równowadze dwie fazy - ciekła i gazowa. Powyżej linii cieczy istnieje tylko faza ciekła, a poniżej linii pary tylko gazowa. Taki diagram fazowy przedstawiony jest na rysunku 2.

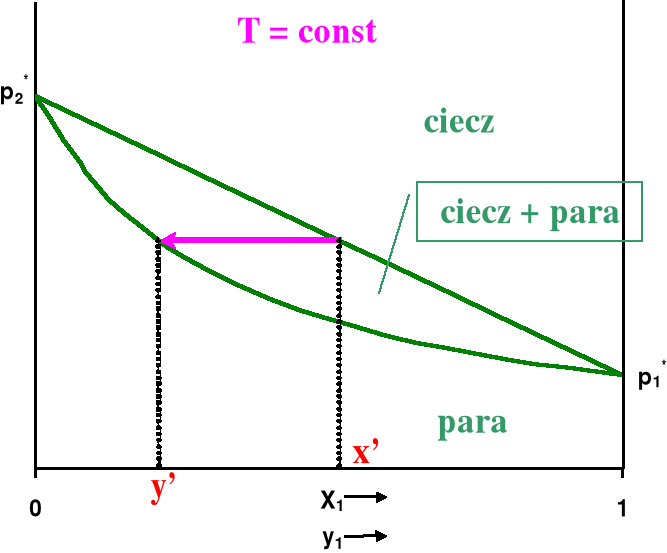
Rysunek 2. Diagram fazowy dla roztworu doskonałego w stałej temperaturze.

Na przykładzie przedstawionym na rysunku 2 składnik 2 ma wyższą prężność par niż składnik 1, jest więc bardziej lotny w danej temperaturze. Jeśli mamy ciecz o składzie x', to skład pary znajdującej się w równowadze z nią znajdujemy kreśląc pozioma linię (różowa strzałka na wykresie) od linii cieczy do linii pary. W tym wypadku w parze będzie więcej składnika 2, bardziej lotnego. Taka zasada obowiązuje zawsze w czasie destylacji, że para jest wzbogacona w składnik bardziej lotny. Możemy też wykreślić zależność temperatury wrzenia takiego układu od składu pary i składu cieczy pod stałym ciśnieniem, co pokazano na rysunku 3.

Rysunek 3. Diagram fazowy dla roztworu doskonałego pod stałym ciśnieniem.

Taki diagram jest podstawą dyskusji destylacji izobarycznej, co bardziej szczegółowo poznajecie na inżynierii procesowej. W naszym przykładzie ciecz 2 jest bardziej lotna, wobec tego pod stałym ciśnieniem ma niższą temperaturę wrzenia od cieczy 1. Skład pary i cieczy pozostających w równowadze znajduje się analogicznie jak w przypadku destylacji izotermicznej. I znowu widać, że para jest wzbogacona w składnik bardziej lotny czyli ten o niższej temperaturze wrzenia.

W przypadku roztworu doskonałego obydwa składniki roztworu traktujemy jednakowo, przyjmujemy dla nich taki sam sposób opisu potencjału chemicznego i tak samo dobieramy stan standardowy. Obecnie przejdziemy do definicji roztworu idealnie rozcieńczonego, gdzie każdy ze składników opisujemy inaczej. Wyróżniamy tu składnik 1 zwany rozpuszczalnikiem i składnik 2 zwany substancją rozpuszczoną.

Roztwór idealnie rozcieńczony (idealny)

Dla rozpuszczalnika dobór stanu standardowego jest taki sam jak w roztworze doskonałym, czyli stan czystego składnika pod danym, stałym ciśnieniem i danej, stałej temperaturze. Natomiast dla substancji rozpuszczonej stan standardowy to stan składnika w roztworze nieskończenie rozcieńczonym, gdy stężenie dąży do zera.
to potencjał chemiczny standardowy.

Z definicji roztworu idealnie rozcieńczonego można wyprowadzić prawo Henry'ego opisujące prężność par substancji rozpuszczonej nad roztworem.

Prawo Henry'ego

K_H w tym wzorze to stała Henry'ego. Oznacza hipotetyczne ciśnienie czystego składnika rozpuszczonego, gdyby zachowywałby się on jak w roztworze nieskończenie rozcieńczonym. Znaczenie stałej Henry'ego pokazane jest na rysunku 4.

Rysunek 4. Sposób wyznaczania stałej Henry'ego.

Aby znaleźć stałą Henry'ego, wykreślamy zależność prężności pary składnika 2 od ułamka molowego. Następnie rysujemy styczną do tej krzywej dla stężenia dążącego do zera. Ekstrapolujemy tą prostą do x₂ = 1 i odczytana tak wartość ciśnienia to poszukiwana stała Henry'ego.

Prawo Henry'ego jest często używane do opisu rozpuszczalności gazów w cieczach w nieco innej postaci.

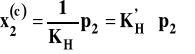
Na rysunku 5 pokazano interpretację stanu standardowego i potencjału chemicznego standardowego dla roztworu doskonałego i idealnie rozcieńczonego. Definicja roztworu doskonałego mówi, że potencjał chemiczny składnika jest liniową funkcją logarytmu naturalnego z jego ułamka molowego w cieczy w całym zakresie stężeń. Wobec tego, gdy ln1 = 0, to na wykresie zależności potencjału chemicznego od lnx mamy poszukiwany potencjał chemiczny standardowy. Natomiast definicja roztworu idealnie rozcieńczonego mówi, że potencjał chemiczny składnika rozpuszczonego jest liniową funkcją logarytmu naturalnego z ułamka molowego, gdy dąży on do zera. Wówczas lnx dąży do minus nieskończoności. Ekstrapolujemy ten fragment zależności linią prostą aż do ln1 = 0 i w ten sposób wyznaczamy potencjał chemiczny standardowy.

Rysunek 5. Stan standardowy i potencjał chemiczny standardowy dla roztworu doskonałego i idealnie rozcieńczonego.

Zarówno roztwór doskonały jak i idealnie rozcieńczony są tylko modelami. Znakomita większość roztworów to roztwory rzeczywiste, do których nie stosuje się żaden z tych modeli. W efekcie można zastosować prawo Henry'ego dla roztworów bardzo rozcieńczonych, a prawo Raoulta, gdy dążymy do czystego składnika (rysunek 6).

Rysunek 6. Porównanie stosowalności prawa Raoulta i prawa Henry'ego dla roztworu rzeczywistego.

Roztwory rzeczywiste mogą wykazywać dodatnie lub ujemne odchylenia od prawa Raoulta. W przypadku odchyleń dodatnich prężność par składników jest zawsze wyższa niż wynikałoby to z prawa Raoulta, a w przypadku odchyleń ujemnych - niższa (rysunek 7).

Rysunek 7. Odchylenia od prawa Raoulta (liniami przerywanymi zaznaczono zależności prężności od składu wynikające z prawa Raoulta).

Opis termodynamiczny roztworów rzeczywistych

Dla roztworów rzeczywistych chcemy, aby potencjał chemiczny składnika był opisany podobnym równaniem, jak dla roztworu doskonałego czy idealnie rozcieńczonego. Ułamek molowy zastępujemy aktywnością, która jest funkcją termodynamiczną ułamka molowego (składu roztworu), temperatury oraz ciśnienia.

Aktywność jest wielkością bezwymiarową. Jest ona powiązana z ułamkiem molowym składnika w roztworze przez współczynnik aktywności oznaczany γ.

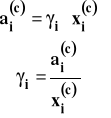
Istnieją dwa sposoby doboru aktywności i współczynnika aktywności.

1. Dobór współczynników aktywności w oparciu o definicję roztworu doskonałego (prawo Raoulta) - symetryczny układ odniesienia

Dla roztworu doskonałego potencjał chemiczny opisany jest wzorem :

który jest spełniany w całym zakresie stężeń, także dla czystego składnika i-tego. A dla roztworu rzeczywistego

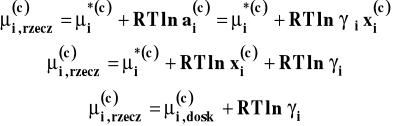
Wobec tego :

Jako stan standardowy składnika i-tego przyjmujemy stan czystego składnika pod stałym ciśnieniem i w stałej temperaturze. Czyli aktywność dąży do ułamka molowego, gdy dążymy do czystego składnika.

Wobec tego, gdy dążymy do czystego składnika i-tego różnica pomiędzy potencjałem chemicznym w roztworze rzeczywistym a potencjałem chemicznym w roztworze doskonałym winna dążyć do zera czyli współczynnik aktywności dąży do jedności.

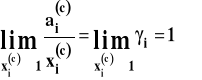
Gdy opieramy się na prawie Raoulta, stan standardowy dal obu składników roztworu przyjmujemy tak samo, jako stan czystej substancji. Dlatego taki układ odniesienia nazywa się symetrycznym.

2. Dobór współczynników aktywności w oparciu o definicję roztworu idealnie rozcieńczonego (prawo Henry'ego) - niesymetryczny układ odniesienia

Jak pamiętamy, w tym wypadku wyróżniamy składnik 1 zwany rozpuszczalnikiem i składnik 2 zwany substancją rozpuszczoną. Potencjał chemiczny rozpuszczalnika opisujemy identycznie jak poprzednio, przyjmując jako stan standardowy stan czystego rozpuszczalnika. Wobec tego dobór aktywności i współczynnika aktywności dla rozpuszczalnika będzie wyglądał identycznie, jak w poprzednim przypadku. Natomiast dla substancji rozpuszczonej potencjał chemiczny opisany jest równaniem :

które słuszne dla bardzo małych ułamków molowych x₂. Stanem standardowym jest teraz stan substancji rozpuszczonej w roztworze nieskończenie rozcieńczonym, gdy stężenie dąży do zera. Dla roztworu rzeczywistego zastępujemy ułamek molowy aktywnością :

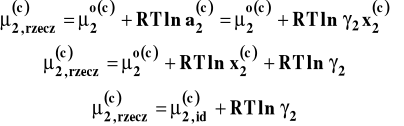
Wobec tego :

Jako stan standardowy substancji rozpuszczonej przyjmujemy jej stan w roztworze nieskończenie rozcieńczonym pod stałym ciśnieniem i w stałej temperaturze. Czyli aktywność dąży do ułamka molowego, gdy dążymy do roztworu nieskończenie rozcieńczonego.

Wobec tego, gdy dążymy do roztworu nieskończenie rozcieńczonego różnica pomiędzy potencjałem chemicznym składnika rozpuszczonego w roztworze idealnie rozcieńczonym a potencjałem chemicznym w roztworze doskonałym winna dążyć do zera czyli współczynnik aktywności dąży do jedności.

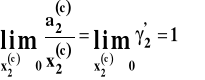
Widzimy więc, dlaczego w tym wypadku mówimy o niesymetrycznym układzie odniesienia. Stan standardowy dla rozpuszczalnika i roztworu jest inny.

Rysunek 8. Dobór stanu standardowego dla roztworów rzeczywistych w oparciu o prawo Raoulta i prawo Henry'ego oraz znaczenie współczynników aktywności

Jeśli substancja rozpuszczona jest cieczą mającą mierzalną prężność par w danej temperaturze, to mamy możliwość wyboru, w jaki sposób chcemy przyjąć dla niej stan standardowy i wyrazić aktywność i współczynniki aktywności. Na rysunku 8 pokazano dobór stanu standardowego i interpretację współczynników aktywności dla obu układów odniesienia dla substancji rozpuszczonej.

Dobór stanu standardowego dla stałej substancji rozpuszczonej - praktyczne współczynniki aktywności

W praktyce mamy bardzo często do czynienia z roztworami, w których substancja rozpuszczona to ciało stałe, praktycznie niewykazujące prężności par (nielotne) i o ograniczonej rozpuszczalności w danym rozpuszczalniku. Stężenie takiej substancji wyrażone postaci ułamka molowego ma bardzo małą wartość i niewygodnie jest się nią posługiwać. Zresztą stężenia roztworów w praktyce wyrażane są jako molowe (jako ilość moli substancji rozpuszczonej na jednostkę objętości roztworu - zwykle 1 dm³) lub molarne (molalne) jako ilość moli substancji rozpuszczonej na 1 kilogram rozpuszczalnika. Aczkolwiek w codziennej praktyce laboratoryjnej używamy stężeń molowych, bo znakomitą większość roztworów robimy w kolbach miarowych, rozpuszczając naważkę substancji w określonej objętości (do kreski), to z punktu widzenia opisu termodynamicznego ten wybór stężenia jest niewygodny. Stężenie molowe bowiem zależy od temperatury, gdyż objętość cieczy rośnie wraz z temperaturą. Jeśli w temperaturze 20ºC zrobimy 1 dm³ roztworu zawierający 1 mol substancji rozpuszczonej, to jego stężenie wyniesie 1 mol/dm³. Gdy roztwór ten ogrzejemy do np. 50ºC, to jego stężenie zmniejszy się, gdyż jego objętość wzrośnie. Wobec tego w opisie zależności własności roztworu od stężenia i temperatury musielibyśmy uwzględnić zależność stężenia od temperatury, co bardzo komplikowałoby wszystkie wzory. Sposób wyrażenia stężenia jako molarnego jest wolny od tej wady, gdyż masa rozpuszczalnika jest stała. Dlatego też w opisie termodynamicznym roztworów lepszym wyborem i stosowanym w nauce jest używanie stężenia molarnego.

Dla roztworu idealnie rozcieńczonego (idealnego) potencjał chemiczny składnika rozpuszczonego wyrażamy wzorem :

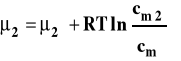
gdzie :
- potencjał chemiczny standardowy
- stężenie standardowe 1 mol/kg
- stężenie molarne substancji rozpuszczonej

Stanem standardowym jest stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/kg w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem. Potencjał chemiczny w tak dobranym stanie standardowym jest potencjałem chemicznym standardowym, którego wartość zależy od temperatury i ciśnienia. Formalnie w wyrazie pod logarytmem dzielenie przez jeden nic nie zmienia, ale robimy tak, aby zredukować jednostkę (pod logarytmem mogą być tylko wartości niemianowane).

Dla roztworu rzeczywistego zamiast stężenia podstawiamy aktywność, która jest funkcją stężenia roztworu, temperatury i ciśnienia.

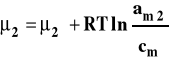
Aktywność można powiązać ze stężeniem przez współczynnik aktywności.

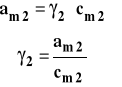
Aktywność i współczynnik aktywności dobieramy tak, aby aktywność dążyła do stężenia, gdy stężenie dąży do zera czyli gdy dążymy do roztworu nieskończenie rozcieńczonego. Współczynnik aktywności dąży wówczas do jedności.

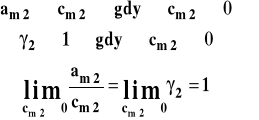
Stanem standardowym jest hipotetyczny stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/kg w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem, gdyby zachowywał się on jak w roztworze idealnie rozcieńczonym. Wybór stanu standardowego i interpretacja potencjału standardowego oraz współczynnika aktywności przedstawione są na rysunkach 9 i 10. Rysunek 9 przedstawia zależność aktywności od stężenia. Stanem odniesienia jest stan składnika w roztworze idealnie rozcieńczonym. Kreślimy więc styczną do tej zależności przy stężeniu zerowym i ekstrapolacja jej wyznacza stan standardowy przy stężeniu 1 mol/kg.

Rysunek 9. Dobór stanu standardowego dla substancji rozpuszczonej w roztworze rzeczywistym, gdy skład wyrażony jest przez stężenie molarne (w mol/kg).

Rysunek 10 pokazuje zależność potencjału chemicznego składnika od stężenia roztworu. I znowu. Ponieważ odniesieniem jest stan składnika w roztworze nieskończenie rozcieńczonym, ekstrapolujemy linia prostą zależność, gdy lnc_m2 dąży do minus nieskończoności. Wartość potencjału chemicznego dla lnc_m2 = 0 (gdy c_m2 = 1) wyznacza nam poszukiwaną wartość potencjału chemicznego standardowego.

Rysunek 10. Interpretacja stanu standardowego i współczynnika aktywności substancji rozpuszczonej w roztworze rzeczywistym, gdy skład wyrażony jest jako stężenie molarne (w mol/kg).

W przypadku użycia stężenia molowego potencjał chemiczny składnika w roztworze idealnym opisujemy równaniem.

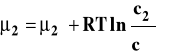
gdzie :
- potencjał chemiczny standardowy
- stężenie standardowe 1 mol/dm³
- stężenie molowe substancji rozpuszczonej

Stanem standardowym jest stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/dm³ w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem. Potencjał chemiczny w tak dobranym stanie standardowym jest potencjałem chemicznym standardowym, którego wartość zależy od temperatury i ciśnienia. Dla roztworu rzeczywistego zamiast stężenia podstawiamy aktywność, która jest funkcją stężenia roztworu, temperatury i ciśnienia.

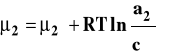
Aktywność można powiązać ze stężeniem przez współczynnik aktywności.

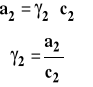
Aktywność i współczynnik aktywności dobieramy tak, aby aktywność dążyła do stężenia, gdy stężenie dąży do zera czyli gdy dążymy do roztworu nieskończenie rozcieńczonego. Współczynnik aktywności dąży wówczas do jedności.

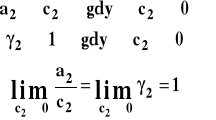
Stanem standardowym jest hipotetyczny stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/dm³ w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem, gdyby zachowywał się on jak w roztworze idealnie rozcieńczonym. Interpretacja stanu standardowego, standardowego potencjału chemicznego i współczynnika aktywności jest analogiczna jak dla przypadku użycia stężenia molarnego i nie będziemy jej tu powtarzać. Współczynniki aktywności określone, gdy wyrażenie na potencjał chemiczny opiera się na stężeniu, nazywamy praktycznymi.

Diagramy fazowe dla równowag ciecz - para w roztworach rzeczywistych

Znamy już diagramy fazowe dla roztworu doskonałego przy stałym ciśnieniu (destylacja izobaryczna) i w stałej temperaturze (destylacja izotermiczna). Wiemy też, że roztwory rzeczywiste wykazują odchylenia od prawa Raoulta, przy czym odchylenia te mogą być dodatnie lub ujemne (rysunek 7). W przypadku niewielkich odchyleń od prawa Raoulta diagramy fazowe dla tych równowag są bardzo podobne jak dla roztworu doskonałego, tylko linia cieczy dla wykresu przy stałej temperaturze nie jest linią prostą.

Rysunek 11. Wykresy fazowe dla układu dwu cieczy o nieograniczonej mieszalności wykazującego niewielkie odstępstwa od prawa Raoulta.

Gdy odchylenia od prawa Raoulta stają się duże, na linii zależności ciśnienia całkowitego w funkcji składu cieczy (linii cieczy) może pojawić się ekstremum - maksimum lub minimum. W ekstremum linia pary styka się z linią cieczy i skład cieczy i pary jest jednakowy. Takie układy nazywane są układami azeotropowymi (azeotropami). Wyróżniamy azeotropy ujemne i dodatnie.

Układy azeotropowe ujemne

Układy azeotropowe ujemne wykazują ujemne odchylenia od prawa Raoulta, posiadają minimum na krzywej zależności prężności pary od składu cieczy. Na linii zależności temperatury wrzenia od składu cieczy pod stałym ciśnieniem mają maksimum. W ekstremum zwanym punktem azeotropowym skład cieczy i pary jest taki sam. Dlatego też roztworu tworzącego układ azeotropowy nie można rozdzielić na składniki przez destylację. W wyniku destylacji otrzymamy zawsze jeden ze składników i roztwór o składzie odpowiadającym punktowi azeotropowemu. Azeotropy ujemne tworzą ciecze, dla których entalpia mieszania jest ujemna _mixH < 0, proces mieszania jest egzotermiczny. Przykładem mogą być układy woda - HNO₃ , woda - HCl. Na rysunku 12 przedstawiono wykresy fazowe dla układu azeotropowego ujemnego.

Rysunek 12. Wykresy fazowe dla układu azeotropowego ujemnego (układ z maksymalną temperaturą wrzenia) : A - punkt azeotropowy.

Układy azeotropowe dodatnie

Układy azeotropowe dodatnie wykazują dodatnie odchylenia od prawa Raoulta, posiadają maksimum na krzywej zależności prężności pary od składu cieczy. Na linii zależności temperatury wrzenia od składu cieczy pod stałym ciśnieniem mają natomiast minimum. Azeotropy dodatnie tworzą zwykle ciecze, dla których entalpia mieszania jest dodatnia _mixH > 0, proces mieszania jest silnie endotermiczny. Od tej reguły istnieje jednak wiele wyjątków. Azeotropy dodatnie tworzone są często przez ciecze różniące się znacznie polarnością, na przykład wodę i mieszające się z nią ciecze organiczne jak alkohole, dla których proces mieszania jest słabo egzotermiczny. Typowym przykładem jest układ woda - etanol, o dużym znaczeniu praktycznym. Każdy, kto dobierał wódkę ze spirytusu, wie że podczas mieszania wody i etanolu wydziela się pewna ilość ciepła, a więc proces mieszania jest egzotermiczny. Mimo to układ ten jest azeotropem dodatnim. Pod ciśnieniem atmosferycznym temperatura wrzenia w punkcie azeotropowym wynosi 78,15ºC, a zawartość etanolu w destylacie 95,58 % wagowo. Dlatego też z cieczy po fermentacji alkoholowej, zawierającej od kilku do kilkunastu % etanolu, można przez destylację frakcyjną uzyskać tylko roztwór o składzie odpowiadającym punktowi azeotropowemu (spirytus rektyfikowany). Aby usunąć z niego wodę i otrzymać etanol bezwodny (spirytus absolutny) trzeba stosować inne metody np. destylację azeotropu z dodatkiem benzenu lub suszenie środkami wiążącymi wodę.

Na rysunku 13 pokazano diagramy fazowe dla układu azeotropowego dodatniego.

Rysunek 13. Wykresy fazowe dla układu azeotropowego dodatniego (układ z minimalną temperaturą wrzenia) : A - punkt azeotropowy.

Układy dwu cieczy o ograniczonej mieszalności ; równowagi ciecz - ciecz w układach dwuskładnikowych ; luka mieszalności

Przyjrzyjmy się nieco bliżej procesowi mieszania dwu cieczy. Gdy powstaje roztwór doskonały entalpia swobodna mieszania, rozumiana jako różnica entalpii swobodnych roztworu i czystych składników przed zmieszaniem, wyraża się wzorem :

Ma ona oczywiście wartość ujemną, gdyż ułamki molowe są mniejsze od jedności czyli logarytmy z nich są ujemne. Jednoznacznie potwierdza to, że proces tworzenia roztworu (mieszanie) jest samorzutny. W przypadku tworzenia roztworu rzeczywistego zamiast ułamków molowych należy podstawić aktywności składników.

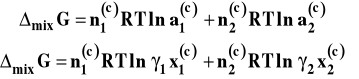
W danej stałej temperaturze i pod stałym ciśnieniem aktywności i współczynniki aktywności zależą od składu roztworu. Powoduje to, że entalpia swobodna mieszania rośnie (choć dalej pozostaje ujemna). Na rysunku 14 pokazano zależność entalpii swobodnej mieszania (liczonej na 1 mol roztworu) od składu. Dla roztworu doskonałego na linii obrazującej tą zależność mamy minimum dla ułamka molowego 0,5 i linia ta jest symetryczna. W miarę odchyleń od doskonałości entalpia swobodna mieszania rośnie, minimum już nie jest dla składu 0,5 ; krzywa staje się niesymetryczna. Gdy odchylenia od doskonałości są duże, na linii pokazującej zależność entalpii swobodnej od składu, pojawiają się dwa lokalne minima (punkty A i B na wykresie) oraz lokalne maksimum. Oznaczałoby to, że w pewnym obszarze od punktu A do B krzywa jest wypukła, a tak być nie może. W obszarze składów odpowiadających punktom A i B układ rozpada się na dwie fazy ciekłe. Każda z nich jest roztworem nasyconym odpowiednio składnika 1 w 2 i składnika 2 w 1. Entalpia swobodna w zakresie od A do B zmienia się liniowo. Skład faz pozostających w równowadze jest niezmienny, zmienia się tylko stosunek pomiędzy ilościami jednej i drugiej fazy. W układzie występuje tak zwana luka mieszalności.

Rysunek 14. Zależność entalpii swobodnej mieszania od składu roztworu - powstawanie luki mieszalności.

Wielkość luki mieszalności (zakres stężeń, przy których układ jest dwufazowy) zależy od temperatury pod danym, stałym ciśnieniem. Wyróżniamy układy z górną krytyczną temperaturą mieszalności i dolną krytyczną temperaturą mieszalności.

Na rysunku 15 pokazano wykres fazowy układu z górną krytyczną temperaturą mieszalności. Są to najczęściej spotykane układy, w których wzajemna rozpuszczalność dwu cieczy wzrasta wraz z temperaturą, a proces mieszania jest endotermiczny.

Rysunek 15. Diagram fazowy dla układu dwu cieczy o ograniczonej mieszalności z górną krytyczną temperaturą mieszalności.

Na rysunku 15 linia A to linia roztworu nasyconego składnika 1 w składniku 2, a linia B to linia roztworu nasyconego 2 w 1. Schodzą się one razem w punkcie odpowiadającym górnej krytycznej temperaturze mieszalności. Powyżej tej temperatury występuje zawsze tylko jedna faza ciekła. Połączone linie A i B rozdzielają całe pole diagramu na dwa obszary. Powyżej i na zewnątrz mamy jedną fazę ciekłą. Natomiast poniżej mamy dwie fazy ciekłe, z których każda jest roztworem nasyconym, odpowiednio 1 w 2 i 2 w 1. Przykładem układów z górną krytyczną temperaturą mieszalności są układy : woda - fenol, woda - furfural.

W przypadku układów z dolną krytyczną temperaturą mieszalności wzajemna rozpuszczalność obu cieczy rośnie wraz ze spadkiem temperatury. Entalpia mieszania w takich układach jest ujemna czyli proces mieszania jest egzotermiczny. Dolna krytyczna temperatura mieszalności występuje w układach dwu cieczy, z których każda jest silnie zasocjowana. Zwykle są to układy woda - amina organiczna np. n-propyloamina lub trietyloamina. Wykres fazowy dla takich układów pokazany jest na rysunku 16.

Rysunek 16. Diagram fazowy dla układu dwu cieczy o ograniczonej mieszalności z dolną krytyczną temperaturą mieszalności.

W tym wypadku poniżej linii A i B mamy do czynienia z roztworem jednorodnym (jedną fazą ciekłą), a powyżej mamy dwie fazy ciekłe, z których każda jest odpowiednio roztworem nasyconym 2 w 1 i 1 w 2.

Istnieją też stosunkowo rzadkie układy, w których występuje zarówno dolna jak i górna krytyczna temperatura mieszalności. Linie roztworów nasyconych A i B tworzą zamkniętą krzywą, wewnątrz której jest obszar występowania dwu faz ciekłych (rysunek 17). Na zewnątrz tego obszaru istnieje tylko jedna faza ciekła. Jak widać na rysunku, składy odpowiadające dolnej i górnej krytycznej temperaturze mieszalności są różne. Typowe przykłady takich układów to : woda - nikotyna lub woda - 2,6-dwumetylopirydyna pod ciśnieniem atmosferycznym. Wiele układów, które pod ciśnieniem atmosferycznym wykazuje górną krytyczną temperaturę mieszalności, pod wysokimi ciśnieniami ma zarówno dolną jak i górną krytyczną temperaturę mieszalności, gdyż wzajemna rozpuszczalność cieczy rośnie wraz ze wzrostem ciśnienia.

Rysunek 17. Diagram fazowy dla układu dwu cieczy o ograniczonej mieszalności z dolną i górną krytyczną temperaturą mieszalności.

Równowaga ciecz -para dla układu dwu cieczy całkowicie się niemieszających ; destylacja z parą wodną

W przypadku, gdy mamy dwie ciecze niemieszające się z sobą, prężność pary każdego ze składników jest taka jak nad czystą cieczą. Układ taki jest jednozmienny, gdyż w równowadze współistnieją trzy fazy (dwie ciekłe i para).

Z układami takimi mamy najczęściej do czynienia w przypadku wody i niepolarnych lub słabo polarnych cieczy organicznych. Całkowita prężność par nad układem dwu cieczy niemieszających się jest sumą prężności obu czystych składników w danej temperaturze.

Na rysunku 18 pokazano zależność prężności par nad cieczą dla takiego układu.

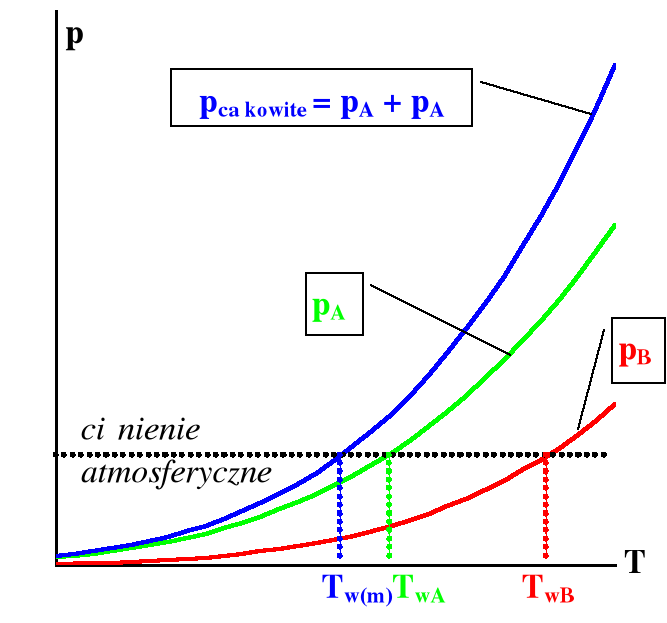
Rysunek 18. Zależność prężności par od temperatury nad układem dwu cieczy niemieszających się z sobą.

Ciecz zaczyna wrzeć, gdy równowagowa prężność par jest co najmniej równa ciśnieniu nad cieczą. Z wykresy na rysunku 18, widać jasno, że temperatura wrzenia mieszaniny dwu cieczy jest niższa niż temperatury wrzenia każdej z nich z osobna. Skład pary czyli destylatu, zależy tylko od stosunku prężności par obu składników w danej temperaturze.

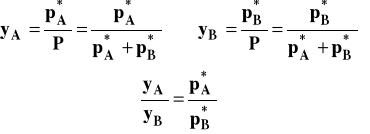
Taką destylację wykorzystuje się często w preparatyce organicznej lub przy otrzymywaniu olejków aromatycznych z surowców naturalnych jako tak zwaną destylację z parą wodną. Jedną z cieczy jest woda, drugą ciecz organiczna o niskiej prężności par (wysokiej temperaturze wrzenia). Do kolby destylacyjnej z materiałem, z którego chcemy oddestylować ciecz organiczną, wprowadza się parę wodną. W odbieralniku zbiera się mieszanina wody i cieczy organicznej, które możemy następnie rozdzielić w rozdzielaczu.

Równowagi ciecz - ciało stałe w układach dwuskładnikowych

Równowagi takie prezentujemy zawsze na diagramach fazowych przedstawiających zależność temperatury topnienia od składu przy stałym ciśnieniu (p = const). Będziemy omawiać cztery podstawowe przypadki takich równowag :

• Całkowita mieszalność obu składników w stanie ciekłym i stałym

• Całkowita mieszalność obu składników w stanie ciekłym i całkowita niemieszalność w stanie stałym

• Całkowita mieszalność obu składników w stanie ciekłym i tworzenie związku przejściowego trwałego tylko w stanie stałym

• Całkowita mieszalność w stanie ciekłym i ograniczona w stanie stałym

Równowaga ciecz - ciało stałe w przypadku całkowitej mieszalności obu składników w stanie ciekłym i stałym

Jeśli oba składniki tworzą roztwory ciekłe i stałe w całym zakresie stężeń, to ich diagram fazowy jest bardzo podobny w kształcie do diagramu dla destylacji izobarycznej. Taki diagram pokazany jest na rysunku 19. Linia oznaczona jako liquidus pokazuje temperaturę topnienia w funkcji składu cieczy, a linia solidus w funkcji składu ciała stałego. Powyżej linii liquidus mamy roztwór ciekły (1 faza), poniżej linii solidus roztwór stały (1 faza). W obszarze ograniczonym liniami solidus i liquidus mamy w równowadze dwie fazy : roztwór stały i roztwór ciekły. Układy takie tworzone są zwykle przez dwie substancje o podobnych wielkościach cząsteczek i krystalizujących w tym samym układzie krystalograficznym. Przykłady takich układów to : Ni - Cu ; AgCl - NaCl ; naftalen - -naftol.

Rysunek 19. Diagram fazowy układu dwuskładnikowego z całkowitą mieszalnością obu składników w stanie stałym i ciekłym, w przypadku zachowania doskonałego lub niewielkich odchyleń od niego.

Poziomą strzałką na tym wykresie połączono punkty odpowiadające składowi cieczy i ciała stałego pozostających w równowadze w danej temperaturze. Jak widać, roztwór stały jest wzbogacony w składnik o wyższej temperaturze topnienia. Diagramy takie są podstawą do dyskusji krystalizacji frakcyjnej wykorzystywanej do na przykład oczyszczania materiałów stosowanych w elektronice.

W przypadku dużych odchyleń w takich układach od doskonałości na liniach solidus i liquidus może pojawić się lokalne ekstremum : maksimum lub minimum. Będziemy mieć odpowiednio układy z minimalną temperaturą topnienia w przypadku dodatnich odchyleń układu od doskonałości oraz z maksymalną temperaturą topnienia w przypadku ujemnych odchyleń od doskonałości. Wykresy fazowe dla takich układów pokazane są na rysunku 20.

Rysunek 20. Diagram fazowy układu dwuskładnikowego z całkowitą mieszalnością obu składników w stanie stałym i ciekłym, w przypadku dużych odchyleń od doskonałości ; a - układ z maksymalną temperaturą topnienia, b - układ z minimalną temperatura topnienia.

Na rysunkach tych linia górna to liqiudus, dolna - solidus. W ekstremum linie solidus i liquidus schodzą się razem w punkcie oznaczonym B na wykresie. W tym punkcie skład fazy ciekłej i stałej jest taki sam. Układy z minimalną temperatura topnienia są popularne. Przykłady to : Cu - Au ; K - Cs ; KCl - KBr ; kwas o-chlorobezoesowy - kwas o-jodobenzoesowy. Układy z maksymalną temperaturą topnienia są bardzo rzadkie.

Równowaga ciecz - ciało stałe w przypadku całkowitej mieszalności obu składników w stanie ciekłym i całkowitej niemieszalności w stanie stały - układy eutektyczne

W stanie ciekłym obydwa składniki mieszają się w sposób nieograniczony tworząc roztwór, jedną fazę ciekłą. Natomiast w stanie stałym nie mieszają się wzajemnie ze sobą. Każdy ze składników tworzy czyste kryształy. Mamy więc możliwość występowania dwu faz stałych. Wykres fazowy dla takiego układu pokazany jest na rysunku 21,

Rysunek 21. Diagram fazowy dla układu z całkowitą mieszalnością w stanie ciekłym i całkowitą niemieszalnością w stanie stałym.

Linie liquidus opisują stężenie roztworów nasyconych odpowiednio składnika 1 w składniku 2 i 2 w 1. Powyżej mamy obszar występowania fazy ciekłej, będącej roztworem nienasyconym. Po lewej i po prawej stronie poniżej linii liquidus mamy obszar współistnienia w równowadze roztworu nasyconego i jednego ze składników w stanie stałym, czyli mamy do czynienia z układami dwufazowymi. Poniżej linii poziomej istnieją w równowadze dwie fazy stałe : czysty składnik 1 i czysty składnik 2. W punkcie oznaczonym E czyli w punkcie eutektycznym współistnieją w równowadze trzy fazy : ciekła (roztwór nasycony) i dwie stałe. Ponieważ cały diagram jest przedstawiony przy założeniu, że ciśnienie jest stałe, to temperatura topnienia i skład układu w punkcie eutektycznym są ściśle określone. Układy tego typu są nazywane układami eutektycznym. Zauważmy że w punkcie eutektycznym temperatura topnienia układu jest najniższa.

Układy eutektyczne są często spotykane. W wielu wypadkach jednym ze składników jest woda, a drugim jakaś substancja stała (sole, cukry, mocznik i inne). Układy eutektyczne mają znaczenie praktycznie. Jednym z doskonale znanych układów tego typu jest układ woda - NaCl. Skład tego układu w punkcie eutektycznym to 0,2242 NaCl molowo, a temperatura topnienia -21,2°C. Dlatego też zimą ulice i jezdnie posypywane są solą, aby śnieg i lód topiły się. Alternatywnie stosuje się też chlorek wapnia. Mieszaninę lodu i soli kuchennej stosuje się też jako mieszaninę chłodzącą. W czasach przed istnieniem lodówek stosowanie takiej mieszaniny pozwalało na produkcję lodów. Inne mieszaniny chłodzące pozwalające osiągać temperatury do około -70ºC to aceton lub etanol + suchy lód (stały CO₂). Jak wspomniano, woda i cukry tworzą też układ eutektyczny. Wykorzystuje się to przy produkcji tak zwanych „lodowych win”. Winogrona zbierane są po przemrożeniu owoców. Wówczas w gronach zamarza część wody, a stężenie cukrów w soku rośnie w wyniku zatężenia. Sok trzeba wyciskać z nich szybko, natychmiast po zbiorze, aby lód nie roztopił się. Powstają w ten sposób aromatyczne, słodkie deserowe wina. Tego typu trunki produkowane są tylko w winnicach na północnym zasięgu uprawy winorośli (Niemcy, Austria, Kanada) i tylko w niektórych latach, gdy są wczesne nocne przymrozki.

Równowaga ciecz - ciało stałe w przypadku całkowitej mieszalności w stanie ciekłym i ograniczonej w stanie stałym

Na rysunku 22 przedstawiono wykres fazowy dla układu, w którym oba składniki w stanie ciekłym mieszają się w sposób nieograniczony, natomiast w stanie stałym występuje luka mieszalności.

Rysunek 22. Diagram fazowy dla układu z nieograniczoną mieszalnością w stanie ciekłym i ograniczoną w stanie stałym.

Znaczenie linii i pól na rysunku 22 :

 - stały, nienasycony roztwór składnika 1 w 2

 - stały, nienasycony roztwór składnika 2 w 1

1 - obszar równowagi cieczy (roztworu nasyconego) i nasyconej stałej fazy 

 - obszar równowagi cieczy (roztworu nasyconego) i nasyconej stałej fazy 

A,F - temperatura topnienia w funkcji składu cieczy (liquidus)

B,G - temperatura topnienia w funkcji składu fazy stałej (solidus)

C,H - linie nasycenia dla roztworów stałych

W punkcie E, który jest też punktem eutektycznym, współistnieją w równowadze : nasycony roztwór ciekły, nasycony roztwór stały składnika 1 w składniku 2 i nasycony roztwór stały składnika 2 w składniku 1 czyli trzy fazy, a więc układ ma jeden stopień swobody. Wobec tego przy ustalonym ciśnieniu skład układu i temperatura topnienia w punkcie eutektycznym są ściśle określone. Przykładem takich układów są : Cu - Ag ; NaCl - CuCl.

Równowaga ciecz- ciało stałe, w przypadku tworzenia się związku trwałego tyko w stanie stałym

W przypadku niektórych układów dwuskładnikowych możliwe jest tworzenie związków pośrednich, które istnieją tylko jako stałe substancje. Schemat wykresu fazowego dla takich układów pokazany jest na rysunku 23.

Rysunek 23. Diagram fazowy dla układu, w którym w stanie stałym powstaje związek pośredni.

Jeśli przyjrzymy się temu wykresowi, to zauważymy, ze jest on złożeniem jakby dwóch wykresów dla układu eutektycznego. Pośrednie maksimum M wyznacza nam temperaturę topnienia związku pośredniego. Ze składu odpowiadającego temu punktowi można wyznaczyć stechiometrię tego związku. W przykładzie na rysunku ułamek molowy dla punktu M to 0,5 czyli oba składniki reagują w stosunku 1:1. Mamy tu dwa punkty eutektyczne. Tego typu układy tworzone są często przez wodę oraz sole lub kwasy lub zasady. Powstające pomiędzy nimi a wodą związki istniejące tylko jako stałe substancje zwane są hydratami. Na przykład kwas siarkowy(VI) H₂SO₄ tworzy z wodą pięć hydratów o różnych składach : H₂SO₄ · 8 H₂O, H₂SO₄ · 6 H₂O, H₂SO₄ · 4 H₂O, H₂SO₄ · 2 H₂O i H₂SO₄ · H₂O.

Przedstawione wykresy fazowe dla równowag ciecz - ciało stałe w układach dwuskładnikowych nie wyczerpują wszystkich możliwych przypadków. Wielokroć diagramy te są znacznie bardziej skomplikowane przez występowanie ograniczonej rozpuszczalności w fazie ciekłej, istnienie rozmaitych form krystalicznych danego związku w stanie stałym. Takie wykresy fazowe są bardzo ważne w rozmaitych zagadnieniach dotyczących metalurgii (np. układ węgiel - żelazo) czy materiałoznawstwa.

Roztwór doskonały to taki, w którym potencjał chemiczny każdego składnika w roztworze można opisać równaniem :

w całym zakresie stężeń

W danej stałej temperaturze prężność pary składnika i-tego nad roztworem doskonałym jest wprost proporcjonalna do jego ułamka molowego w cieczy, a współczynnikiem proporcjonalności jest prężność par czystego składnika w tej temperaturze.

p

p

T = const

P

p₁

0 x_1(c) → 1

1 ← x_2(c) 0

p₂

linia cieczy

linia pary

T

linia cieczy

linia pary

T

y' x'

T₂^o

T₁^o

ciecz + para

ciecz

para

0 x₁ → 1 y₁ →

p = const

Roztwór idealnie rozcieńczony to taki, w którym potencjał chemiczny rozpuszczalnika w roztworze można opisać równaniem :

w całym zakresie stężeń

a potencjał chemiczny substancji rozpuszczonej :

przy stężeniach bliskich zeru

W danej stałej temperaturze prężność pary składnika rozpuszczonego nad roztworem idealnie rozcieńczonym jest wprost proporcjonalna do jego ułamka molowego w cieczy, a współczynnik proporcjonalności to stała Henry'ego.

0 x₂ → 1

p

p

K_H

T = const

roztwór doskonały roztwór idealnie rozcieńczony

p₂*

p

p





ln x₂

ln x₂

0

0

K_H

roztwór doskonały

(prawo Raoulta)

roztwór idealnie rozcieńczony

(prawo Henry'ego)

0 x₂ → 1

T = const

dodatnie ujemne

T = const

p

p

p

p

0 x₁ → 1

0 x₁ → 1

prawo Henry'ego

prawo Raoulta

1

a₂



0

ln x₂

RT lnγ_

RT lnγ_'

0

roztwór idealnie rozcieńczony

hipotetyczny stan standardowy

roztwór rzeczywisty

c_m2

roztwór rzeczywisty

roztwór idealnie rozcieńczony

0 ln c_m2



odchylenia dodatnie

odchylenia ujemne

ciecz i para w równowadze

p

p

p

p

para

para

ciecz

ciecz

0 x₁ → 1

0 x₁ → 1

T=const

T

T

T

p

p

A

A

0 x₁ → 1

0 x₁ → 1

para

para

ciecz

ciecz

T = const p = const

p

p

A

para

ciecz

A

para

ciecz

0 x₁ → 1

0 x₁ → 1

T

T = const p = const

B

A

0

_mixG_m

T

p, T = const

duże odchylenia od zachowania doskonałego

małe odchylenia od zachowania doskonałego

roztwór doskonały

0 x₁ → 1

T

T

x_GM

p = const

0 x₁ → 1

B

A

GKTM

dwie fazy ciekłe

jedna faza ciekła

T_GM

T

x_DM

p = const

0 x₁ → 1

A

B

DKTM

dwie fazy ciekłe

jedna faza ciekła

T_DM

T

T

x_DM

x_GM

T_DM

DKTM

p = const

0 x₁ → 1

B

A

GKTM

dwie fazy ciekłe

jedna faza ciekła

T_GM

ciecz + ciało stałe

T

x'_(c) x'_(s)

solidus

liquidus

ciecz

ciało stałe

T

0 x₁ → 1

ciecz + ciało stałe

x_B

x_B

T

T

T

T

B

0 x₁ → 1

b

ciało stałe

ciecz

B

0 x₁ → 1

a

ciało stałe

ciecz

0 x₁ → 1

T

roztwór nasycony 2 w 1

ciecz - roztwór nienasycony

czyste stałe 1 i 2

T

E

roztwór nasycony 1 w 2

roztwór nasycony i czysty stały 2

roztwór nasycony i czysty stały 1

liquidus

T

H

G

F

C

B

A

2

1





E

0 x₁ → 1

ciecz - roztwór nienasycony

nasycone

stała faza  i

stała faza 

T

stały 1 i stały związek 12

E₂

stały 2 i stały związek 12

E₁

T

T

T_M

ciecz - roztwór nienasycony

M

0 x₁ → 1

---