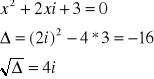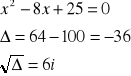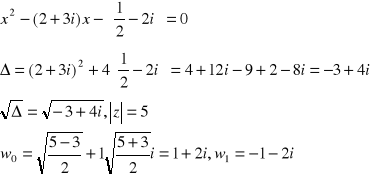Liczby zespolone - ciąg dalszy z dnia 13.11.2010.

Pierwiastkowanie liczb zespolonych.

Każdą liczbę zespoloną „w” spełniającą równanie
, nazywamy pierwiastkiem stopnia „n” z liczby zespolonej „z” i oznaczamy
.

Istnieje dokładnie „n” różnych pierwiastków n-tego stopnia
z liczby zespolonej
.

Jeżeli
, to:

Przykład:

Oblicz pierwiastek trzeciego stopnia -
- dla
.

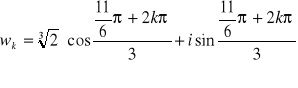
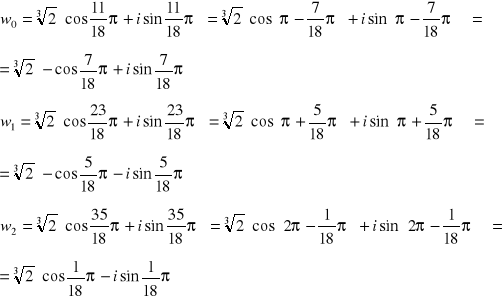
Pierwiastki kwadratowe liczby zespolonej
można obliczyć bez konieczności zamiany tej liczby na postać trygonometryczną. Należy rozpatrzyć trzy przypadki (w zależności od wartości liczb „a” i „b”):

1. 
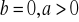
   - liczba zespolona jest liczbą rzeczywistą dodatnią. Wtedy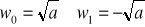
   .

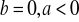
2. 
   - liczba zespolona jest liczbą rzeczywistą ujemną.
   Wtedy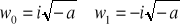
   .

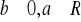
3. 
   
   - liczba jest liczbą zespoloną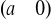
   lub urojona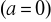
   .
   Wtedy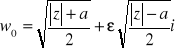
   

(epsilon):

- +1 dla
,

- -1 dla
.

Przykład:

Oblicz pierwiastek
.

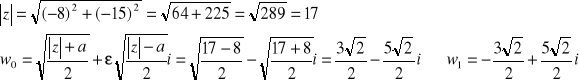
Można również obliczyć pierwiastki drugiego stopnia, korzystając z innej metody.

Przykład.

Jednym z pierwiastków będzie liczba zespolona.

, zatem

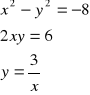
- odpada bo

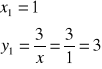
Rozwiązywanie równań.

1. Równania kwadratowe - mają w dziedzinie liczb zespolonych zawsze dwa pierwiastki.

Przykład 1.

1. 
   
   
   
   
   
   
   
   

2. 
   
   
   
   
   
   
   

3. 
   
   
   
   
   

2. 
   
   Inne równania.

Przykład.

1. 
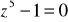
   - jest to tzw. równanie dwumienne typu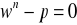
   .
   
   

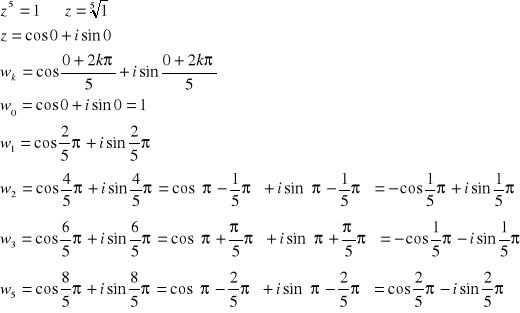
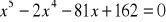
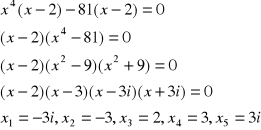
2. 
   

Postać wykładnicza liczb zespolonych.

Liczbę zespoloną
można przedstawić jako:
.

Liczba sprzężona:

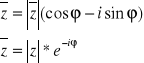
Zależność pomiędzy
oraz
i
określają wzory Eulera:

.

Pierwiastki zespolone.

Przykład.

Przedstaw w postaci wykładniczej liczbę
.

Zastosowanie liczb zespolonych w geometrii.

1. 
   Wzory na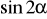
   i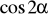
   .
   
   
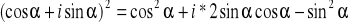
   Ze wzoru de Moivre'a: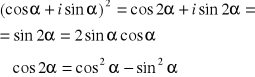
   
   

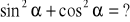
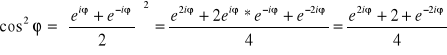
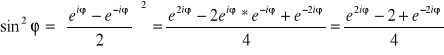
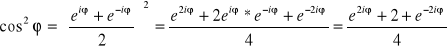
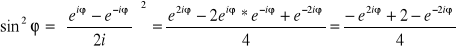
2. 
   
   

! NAJPIĘKNIEJSZY WZÓR MATEMATYKI !

Łączy w sobie pięć stałych matematycznych:

oraz

Notatka autora: legenda głosi, że ludzie ze skrzywioną psychiką podniecają się na samą myśl o nim …

y

x

-1

!

x

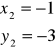
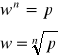
1

y

---