WOJSKOWA AKADEMIA TECHNICZNA

im. JAROSŁAWA DĄBROWSKIEGO

Laboratorium fizyki ogólnej

Sprawozdanie z ćwiczenia laboratoryjnego

Nr 21

Warszawa dn. 19.11.2004

Tytuł: BADANIE DRGAŃ RELAKSACYJNYCH

Wykonał: Szymon Kącik i Sławomir Kowalczyk Prowadzący: dr inż. Wiktor Piecek

Grupa: Eo4D11 Ocena przygotowania do zajęć:

Ocena końcowa:

1.Opis teoretyczny

Do drgań zwanych relaksacyjnymi należą drgania półkształtne, są to drgania znacznie różniące się od harmonicznych, powstające w różnych samowzbudnych układach fizycznych.

Przykład prostego mechanicznego układu samowzbudnego jest pokazany na rysunku (rys. 1). Zbiornik zamocowany na poziomej osi wypełnia się stopniowo wodą. Gdy środek cieżkości zbiornika podniesie się nieco powyżej osi obrotu, równowaga staje się chwiejna. Pod wpływem strumia wody, który pada na boczną ściankę zbiornika przechyla się i woda wylewa się z niego. Zbiornik wraca do położenia pierwotnego i zjawisko powtarza się od nowa.

Podobne drgania piłowe występują w lampie oscyloskopowej.

Rys.1 Mechaniczny układ samowzbudny

Drgania relaksacyjne to drganie, w których wzrosty i spadki napięć następują

w sposób wykładniczy. Zazwyczaj (tak, jak w ćwiczeniu) do ich wytwarzania stosuje się proces ładowania i rozładowywania kondensatora rezystorem.

Po zamknięciu kluczem obwodu zawierającego: źródło siły elektromotorycznej E, rezystor R oraz kondensator C następuje ładowanie kondensatora. Korzystając z drugiego prawa Kirchhoffa otrzymamy:

(1)

Zważywszy, że

(2)

otrzymujemy równanie różniczkowe, które rozwiązujemy względem Q:

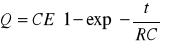
(3)

Obliczając pochodną dQ po dt otrzymujemy ostatecznie:

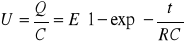
(4)-- napięcie na ładowanym kondensatorze.

Wielkość RC ma wymiar czasu i nazywa się stałą czasową obwodu, która jest równa czasowi, w jakim ładunek na kondensatorze powiększa się o czynnik 1-exp[-1]
jego wartości w stanie równowagi.

Po naładowaniu kondensatora obwód łączymy tak, żeby nie zawierał źródła SEM. W takiej sytuacji będzie zachodziło rozładowywanie kondensatora rezystancją R.

Równanie obwodu ma postać:

(5)

Otrzymujemy równanie różniczkowe i rozwiązujemy je względem Q:

(6)

Wyznaczamy U:

(7)

Jest to napięcie na okładkach kondensatora przy jego rozładowywaniu.

Zależności napięcia na okładkach kondensatora od czasu dana jest wzorem

- podczas ładowania: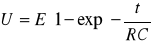
(8)

- podczas rozładowywania:
(9)

Cykliczne przełączanie klucza w obwodzie tak, aby kondensator już to ładował się, już to rozładowywał wymusi powstanie w obwodzie drgań relaksacyjnych. (W ćwiczeniu funkcję klucza spełnia neonówka).

Neonówka ma dwie elektrody pokryte warstwą metalu łatwo emitującego elektrony. Przy niwielkim napięciu na elektrodach prąd nie popłynie w neonówce. Po przekroczeniu wartości napięcia zapłonowego U_z przez lampę popłynie prąd o natężeniu ograniczonym tylko rezystancją zewnętrzną. Gdy napięcie na elektrodach spadnie poniżej napięcia gaśnięcia U_g lampa ponownie nie przewodzi prądu.

Czas t₁ narastania napięcia na kondensatorze od U_g do U_z jest znacznie dłuższy od czasu jego opadania. Korzystając z powyższych zależności możemy wyznaczyć wartości t₁ i t₂.

(10)

oraz

(11) R_n-rezystancja neonówki

Okres drgań relaksacyjnych T=t₁+t₂.

Ponieważ t₁>>t₂ więcokres drgań w tym ćwiczeniu laboratoryjnym dany jest wzorem :

(12) U_z - napięcie zapłonu neonówki; U_g - napięcie gaśnięcia

Poprzez podłączanie różnych oporników i kondensatorów otrzymamy całą rodzinę drgań relaksacyjnych. Możliwe będzie także znalezienie pojemności nieznanego kondensatora.

Najprostszy schemat układu do wytwarzania drgań relaksacyjnych:

Schemat 1. Układ do wytwarzania drgań relaksacyjnych

2. Pomiary

Tabela zawiera pomiary okresów 1000 drgnięć, przy zadanych rezystancjach, oraz przy znanych pojemnościach kondensatorów i jednej nieznanej (C_x). Tabela zawiera również wartość średnią jednego drgnięcia, obliczoną jako średnią arytmetyczną z pięciu pomiarów 100 okresów.

Tab. 1 Pomiar okresu drgań relaksacyjnych dla zadanych pojemności w obwodzie

Opór	Pojemność	T1[s]	T2[s]	T3[s]	T4[s]	T5[s]	Tśr [ms]
R1= 500 kΩ	C1= 5.6 nF	3,538	3,690	3,703	3,794	3,892	3,723
		C2= 8.2 nF	4,606	4,690	4,711	4,775	4,778	4,712
		C3= 10.0 nF	5,274	5,277	5,292	5,331	5,378	5,310
		C4=14.7 nF	6,873	6,900	6,954	6,957	6,951	6,927
		C5=15.8 nF	7,334	7,333	7,390	7,397	7,410	7,373
		C6=17.3 nF	7,993	7,993	8,005	8,015	8,074	8,016
		Cx	6,558	6,576	6,573	6,545	6,596	6,370
	R2= 600 kΩ	C1= 5.6 nF	5,014	5,038	5,016	5,051	5,037	5,031
		C2= 8.2 nF	5,970	6,039	6,030	6,038	6,016	6,019
		C3= 10 nF	6,606	6,610	6,651	6,670	6,732	6,654
		C4=14.7 nF	8,493	8,549	8,549	8,501	8,536	8,526
		C5=15.8 nF	8,939	8,974	8,970	8,911	8,939	8,947
		C6=17.3 nF	9,570	9,548	9,578	9,590	9,619	9,581
		Cx	7,737	7,779	7,799	7,833	7,833	7,796

Pomiary przeprowadzone zostały dla dwóch rezystancji 500k i 600k Dla każdej pojemności kondensatora przeprowadzonych zostało po pięć pomiarów okresów drgań.

3. Obliczenia

• Dla R₁=500[kΩ]

Ponieważ funkcja T=f(C) jest teoretycznie prostą (zależność 12), posługując się metodą Gaussa najmniejszych kwadratów znajdujemy parametry a i b optymalnie poprowadzonej po punktach pomiarowych prostej (tzw. aproksymacja wykresu).

Równanie szukanej prostej ma postać:

Obliczam współczynniki a oraz b metodą Gaussa najmniejszych kwadratów.

Tabela 2. Obliczenie sumy poszczególnych wartości niezbędnych od obliczenia współczynników a oraz b.

n	x	y	xy	x^2	y^2
1	5,6	3,723	20,849	31,4	13,861
2	8,2	4,712	38,638	67,2	22,203
3	10	5,31	53,100	100,0	28,196
4	14,7	6,927	101,827	216,1	47,983
5	15,8	7,373	116,493	249,6	54,361
6	17,3	8,016	138,677	299,3	64,256
	71,6	36,061	469,584	963,6	230,860

Obliczamy także wartość wyrażenia
, która wynosi

Więc:

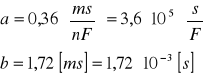
Obliczamy nieznaną pojemność kondensatora C_x

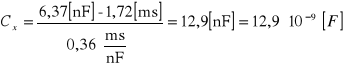
Obliczenie odchyleń standardowych wartości współczynnika a (σ_a) oraz przesunięcia b (σ_b) zależności

σ_a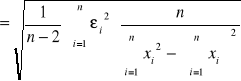

σ_b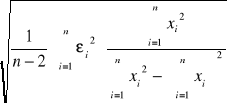

Otrzynujemy

σ_a

σ_b

Obliczenie średniego błędu kwadratowego σ_x

σ_x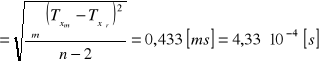

Obliczenie średniego błędu kwadratowego σT_x

σC_x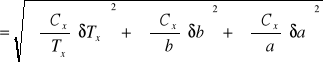

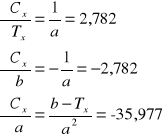
σC_x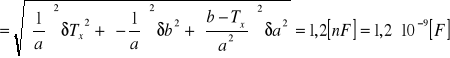

Analogicznie postępujemy dla R₂=600[kΩ], zestawienie wyników znajduje się w tabeli poniżej.

Tab. 3 Zestawienie otrzymanych wyników

R	a	b[s]	Cx[F]	σa	σb[s]	σTx[s]	σ Cx [F]
R1=500
R2=600

4. Wnioski

Obserwując wykresy, można stwierdzić, że wzraz ze wzrostem pojemności wzroście ulega także okres drgań.

Otrzymane pojemności wyniosły dla R₁=500

Oraz dla R₂=600

Na dokładność pomiarów w dużej mierze miała wpływ dokładność zastosowanych urządzeń pomiarowych, czas podawany był z dokładnością do 0,001s, aby zwiększyć precyzje obliczeń powinno się wykorzystać znacznie dokładniejsze urządzenia.

Z wyników przeprowadzonego doświadczenie otrzymujemy, że pojemność nieznanego kondensatora wynosi C_x= 12,8
0,2 [nF]

Szymon Kącik i Sławomir Kowalczyk ćw. laboratoryjne nr 21

rezystancja R

źródło

prądu U

kondensator C

neonówka

---