WOJSKOWA AKADEMIA TECHNICZNA

Im. JAROSŁAWA DĄBROWSKIEGO

Laboratorium Fizyki Ogólnej

Sprawozdanie z ćwiczenia laboratoryjnego

Nr 15

Tytuł: Pomiar siły elektromotorycznej Warszawa dn. 19.11.2004

ogniwa i charakterystyka jego pracy

Wykonali: Paweł Drążyk i Mariusz Fornal Prowadzący: dr inż. Wiktor Piecek

Grupa: E04D11 Ocena przygotowania do zajęć:

Ocena końcowa:

I WSTĘP TEORETYCZNY

Celem doświadczenia jest wyznaczenie siły elektromotorycznej i charakterystyki pracy danego ogniwa. Zanim jednak przejdę do opisu doświadczenia, to muszę napisać, czym jest ta siła.

W źródłach zachodzą procesy rozdzielające ładunki. To powoduje powstanie napięcia na źródle. Przyczynami tego zjawiska mogą być różne procesy chemiczne, elektromagnetyczne, termoelektryczne, bądź fotoelektryczne. To napięcie związane jest bezpośrednio z polem elektrycznym
które również jest tworzone w źródle. Nośniki prądu poruszają się w tym polu, a za ich ruch odpowiedzialna jest siła elektromotoryczna 
. Pole to równe jest:

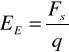
(1.1),

gdzie
to ładunek. Żeby czerpać prąd z ogniwa, pole to musi być większe od pola elektrostatycznego
.

W fizyce siła elektromotoryczna (
) to zdolności do generowania prądu elektrycznego przez układy elektromagnetyczne i elektrochemiczne. Jednostką SEM jest Wolt. Nie jest ona siłą w sensie normalnej, fizycznej definicji tego słowa, a nazwa ta jest swoistą pozostałością historyczną.. Największą możliwą wartość siły elektromotorycznej możemy uzyskać, gdy nie pobieramy prądu ze źródła. W przeciwnym wypadku mierzymy napięcie
równe:

(1.2),

gdzie
to siła elektromotoryczna źródła,
prąd płynący przez obwód, a
to opór wewnętrzny źródła. Przy obciążeniu źródła możemy zauważyć, że napicie na jego rezystancji wzrasta, a to na jego biegunach staje się mniejsze od siły elektromotorycznej
, im silniej obciążone jest źródło. To zjawisko zmniejszana się napięcia na biegunach wraz ze wzrostem obciążenia nazywamy charakterystyką pracy źródła. Zależy ona od oporu wewnętrznego
.

Najprostszą metodą wyznaczania siły elektromotorycznej jest metoda kompensacyjna. Ideowy schemat układu pomiarowego zamieszczam na ryc. 1

W układzie tym napięcie źródła
jest równoważone napięciem
uzyskanym z dzielnika napięcia
. Źródło zasilające musi być większe od siły elektromotorycznej
, oraz włączone do obwodu przeciwnie. Wtedy:

(1.3).

W tej sytuacji przez mierzoną barierę nie przepływa prąd, więc faktycznie dokonujemy pomiaru siły elektromotorycznej. Ta metoda jest metodą bezpośrednią i wymaga dokładnej znajomości napięcia zasilającego 
.

Bardziej dokładnym sposobem wyznaczania siły elektromotorycznej jest metoda kompensacyjno-porównawcza. Nie wymaga ona znajomości napięcia
. Porównuje się tu siłę elektromotoryczną z siłą elektromotoryczną ogniwa wzorcowego o znanej wartości
. Schemat układu przedstawiam na ryc. 2.

Początkowo należy przeprowadzić kompensację układu z wzorcową siłą elektromotoryczną i otrzymamy wynik:

(1.4).

Następnie przeprowadzamy kompensację układu z badaną siłą elektromotoryczną i stąd:

(1.5)

Dzieląc oba równania stronami otrzymujemy, że:

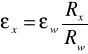
(1.6)

II WYKONYWANE CZYNNOŚCI I WYNIKI POMIARÓW

Pomiaru siły elektromotorycznej dokonujemy przez kompensowanie napięć. Należy tak dopasować opór, by wskazówka galwanometru pozostała w położeniu początkowym i wtedy odczytać wartość napięcia. Pomiar powtórzyć kilkanaście razy dla napięcia pomocniczego 2V (druga kolumna, wyniki należy przemnożyć, przez 5)

By wyznaczyć charakterystykę pracy źródła należy ustawić powtórzyć powyższe czynności ustawiając wartość prądu z przedziału 0,5 - 2,5 mA. Dla każdego natężenia wykonać co najmniej pięć pomiarów (czwarta kolumna tabel, wyniki uśrednić i przemnożyć przez pięć). Otrzymane wyniki zamieszczam w Tabeli 1

Tabela nr 1 Wyniki pomiarów
Lp.	U[mV]	I[mA]	U[mV]
1	931,36	0,5	927,83
						927,83
						927,78
			2	931,28		927,78
						927,77
			3	931,28	1,0	925,49
						925,49
						925,49
			4	931,23		925,48
						925,49
			5	931,20	1,5	923,79
						923,80
						923,87
			6	931,20		923,89
						923,93
			7	931,20	2,0	922,59
						922,80
						922,79
			8	931,21		922,82
						922,82
			9	931,23	2,5	921,67
						921,67
						921,68
			10	931,19		921,68
						921,67
Średnia x5			Każdy wynik x5

III OBLICZENIA I ANALIZA DOKŁADNOŚCI WYNIKÓW

Średnia siła elektromotoryczna źródła wyniosła
.

Średni błąd kwadratowy wynosi:

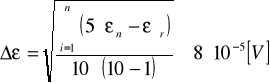
Z zależności mierzonego napięcia do natężenia (1.2) wyznaczam rezystancję wewnętrzną metodą najmniejszych kwadratów. Niezbędne zależności zamieszczam w tabeli 2.

Tabela 2. Podstawowe wartości niezbędne do metody najmniejszych kwadratów.
Nr pomiaru	-I [mA]	- U [mV]	IU	I^2	U^2
1	0,5	4 639	2 320	0,25	21 520
2	1,0	4 627	4 627	1,00	21 409
3	1,5	4 619	6 929	2,25	21 335
4	2,0	4 614	9 228	4,00	21 289
5	2,5	4 608	11 520	6,25	21 234
	7,5	23 107	34 623	13,75	106 787

Obliczam średni współczynnik kierunkowy
i średnią wartość wyrazu wolnego
prostej opisanej wzorem 1.2:

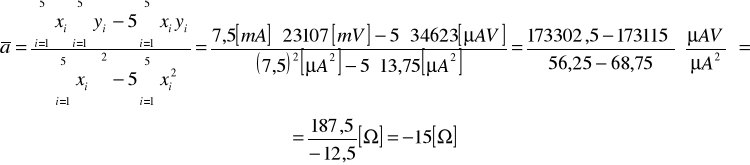
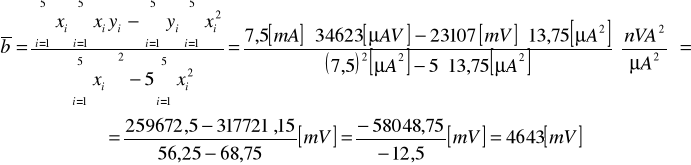
Stąd:

Następnie obliczam odchylenie standardowe tych wartości:

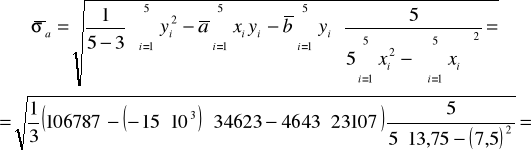
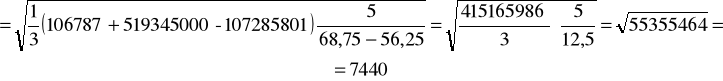
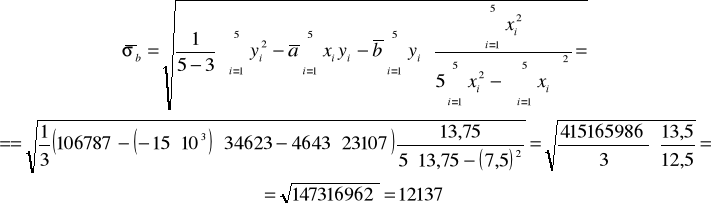
W rezultacie:

,

Poszukiwana prosta zależności 1.2 będzie miała postać:

Zależność przedstawiam na Wykresie 1, który zamieszczam w załączniku.

Dla wszystkich napięć obliczam moc czerpaną ze źródła
z ze wzoru
i moc wydzielaną na rezystancji
, a wyniki zamieszczam w Tabeli 3.

Tabela 3. Moc praktyczna
Punkt pomiarowy
1	0,5	4 639	2,3	8,5
2	1	4 627	4,6	29
3	1,5	4619	6,9	55,5
4	2	4614	9,2	84
5	2,5	4608	11,5	120

Następnie wyliczam teoretyczne wyniki dla tych punktów pomiarowych zgodnie ze wzorami:

i

Wyniki obliczeń zamieszczam w Tabeli 4.

Tabela 4. Moc teoretyczna
Punkt pomiarowy
1	0,5	4 639	2,3	3,7
2	1	4 627	4,6	15
3	1,5	4 619	6,9	33,7
4	2	4 614	9,2	60
5	2,5	4 608	11,5	93,7

Z zależności 1.2 policzyliśmy osobno wartość oporu dla każdego punktu pomiarowego. Uzyskane wartości umieszczamy w Tabeli 5.

Tabela 5. Wartości oporu dla punktów pomiarowych
Punkt pomiarowy			R[Ω]
1	0,5	4 639	34,38
2	1	4 627	29,19
3	1,5	4 619	24,79
4	2	4 614	21,59
5	2,5	4 608	13,27

Zależności praktycznych zamieszczam na Wykresie 2, a teoretycznych Wykresie 3.

IV OMÓWIENIE WYNIKÓW ĆWICZENIA

W trakcie badania siły elektromotorycznej baterii uzyskaliśmy dwie wartości: jedną obliczoną przez uśrednienie pomiarów
i wyznaczoną z przecięcia krzywej
. Napięcie znamionowe wynosi 4,6 V. Bateria przez nas badana była baterią cynkowo - węglową. Mimo, iż są one najtańszymi dostępnymi na rynku, to charakteryzują się niewielką gęstość energii - charakteryzują się także bardzo słaba wydajnością w zastosowaniach wymagających dużych (powyżej 100mA) natężeń prądu.

Wykres 2 pokazuje, że moc wytworzona na oporze jest podobna do przewidywanej. Wykres 3 natomiast pokazuje, iż teoretyczna wartość pracy źródła jest około półtora razy mniejsza od wyliczonej przez nas. Sądzimy, że te różnice spowodowane są zmianami oporu wewnętrznego źródła.

V BIBLIOGRAFIA

• http://www.baterie.batteries.pl/bat_zn.html

• www.wic.wat.edu.pl/

Paweł Drążyk, Mariusz Fornal Strona 7 ćwiczenie nr 15

Ryc. 2 Ilustracja metody kompensacyjno-porównawczej

Ryc. 1. Zasada pomiaru napięcia na źródle metodą kompensacyjną

---