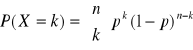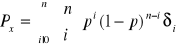ROZKŁAD ZMIENNEJ LOSOWEJ

B

Tw:
jest miarą zupełną i unormowaną na rodzinie zbiorów borelowskich (B
)

Dow:

1. 
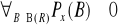
   , bo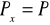
   , a P-miara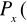

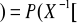
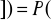
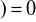
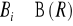
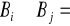
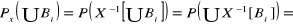
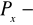
2. 
   ∅
   ∅
   ∅
   

3. 
   ,
   ∅ (
   )
   

4. 
   miara zupełna

Wniosek:
przestrzeń probabilistyczna

Def: Miarę
nazywamy rozkładem zmiennej losowej X.

Tw:
- przestrzeń probabilistyczna

zmienna losowa

- skończona lub przeliczalna liczba wartości zmiennej losowej

Teza:
,

Dow:

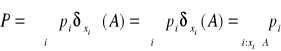
, bo dla

Def: Jeżeli zmienna losowa X przyjmuje skończoną lub przeliczalną ilość wartości, to wówczas mówimy, że rozkład zmiennej losowej jest dyskretny.

Np1: rozkład dwupunktowy

Np2: rozkład Bernoulliego

Np3:

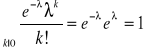
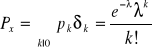
rozkład Poissona z parametrem

Całka względem miary:

przestrzeń z miarą
.

Def: Mówimy, że f jest
prostą jeżeli

1. przyjmuje skończoną liczbę wartości

2. 
   

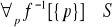
Tw:
, f - nieujemna

- prosta

,
ciąg rosnący, tzn.

Def:
funkcja
prosta przyjmująca wartości:
.

Całkę z funkcji f względem miary
nazywamy wyrażenie
.

Def:
,
oraz istnieje ciąg
taki, że
i
(

prosta) to całką z funkcji f względem miary
nazywamy
.

- dowolna funkcja (niekoniecznie
)

Def:
nazywamy częścią dodatnią f.

nazywamy częścią ujemną f.

Wówczas

,

Np.:

Def:
; Całką z funkcji f nazywamy różnicę całek
.

Jeżeli przynajmniej jedna z całek
lub
jest skończona, to mówimy, ze f jest całkowalna.

Jeżeli obydwie są skończone, to f jest sumowalna.

Uwaga: funkcja jest sumowalna ⇔
- jest skończona.

Def:

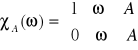
- funkcja charakterystyczna zbioru A [chi]

Def:

Uwaga: Jeśli
(miara Lebesque'a) to
(opuszczamy
)

Tw:	∅ ( ) Jeżeli i , to Jeżeli dwie funkcje f i g różnią się tylko na zbiorze miary zero, to

Tw: Jeżeli funkcja f jest funkcją całkowalną w sensie Riemanna i
, to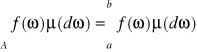
.

Def:

.

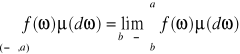
Tw: Jeżeli
- przestrzeń z miarą,
-
mierzalna, nieujemna oraz
to
jest miarą.

Jeżeli dodatkowo
, to wówczas
jest miarą unormowaną.

Def: Miarę
nazywamy iloczynem miary
i funkcji f i oznaczamy
.

Tw:

Funkcja g jest całkowalna względem
⇔ funkcja g jest całkowalna względem
i zachodzi
.

Def: Dana
- przestrzeń probabilistyczna

- zmienna losowa

Jeżeli istnieje nieujemna funkcja
sumowalna względem miary Lebesque'a (
) taka, że
, to mówimy, że zmienna losowa ma rozkład ciągły i f jest gęstością tego rozkładu.

Wniosek: Aby f miała być gęstością rozkładu musi spełniać warunki:

1. 
   

2. 
   

Np.: Funkcja nie jest R-całkowalna, ale jest L-całkowalna:

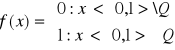
zbiór liczb wymiernych

, bo

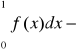
nieokreślona

4

Luke Rachunek prawdopodobieństwa-wykład 12.3.2k+1

---