MIKROSKOP

Celem ćwiczenia jest zrozumienie podstaw działania mikroskopu oraz  zdobycie praktycznych umiejętności obsługi mikroskopu i umiejętności  wyznaczenia wielkości obserwowanego obiektu na podstawie ludzkiego włosa.

ZALECANA LITERATURA: [2], [4], [8], [12], [13], [17], [20], [23]

ZAGADNIENIA:

1. 1.      Optyka geometryczna: odbicie, załamanie, względny i bezwzględny współczynnik załamania, całkowite wewnętrzne odbicie.

2. 2.      Soczewki: konstrukcja obrazu, wzór soczewkowy, zdolność skupiająca, wpływ środowiska otaczającego soczewkę na jej ogniskową.

3. 3.      Przejście światła przez układ optyczny oka; wady wzroku i ich korekcja.

4. 4.      Mikroskop, konstrukcja obrazu w mikroskopie, zdolność rozdzielcza, powiększenie.

5. 5.      Do czego służy olejek immersyjny?

6. 6.      Niepewności pomiarowe - błąd bezwzględny, względny, metoda pochodnej logarytmicznej

OPIS TEORETYCZNY:

Konstrukcja obrazu w mikroskopie, zdolność rozdzielcza i powiększenie mikroskopu. Wady wzroku i ich korekcja.

 

1. 1)Odbicie światła, zjawisko zmiany kierunku rozprzestrzeniania się promieni świetlnych zachodzące na granicy dwóch ośrodków, przy czym gdy co najmniej jeden z nich jest przezroczysty.

2)Załamanie światła jest zmianą kierunku rozchodzenia się fali świetlnej rozprzestrzeniającej się w ośrodku optycznie niejednorodnym. Promień świetlny przechodząc z ośrodka 1 do 2 zmienia prędkość fali, a co za tym idzie także jej długość. Dla płaskiej, nieskończonej granicy 2 różnych, jednorodnych, izotropowych (wykazujący we wszystkich kierunkach jednakowe właściwości fizyczne) i nieabsorbujących (niepochłaniających) ośrodków, kierunek rozchodzenia się fali załamanej jest określony prawami odbicia i załamania.





W myśl powyższych praw, kierunki rozchodzenia się fal: padającej, odbitej i załamanej oraz prostopadłej padania leżą w jednej płaszczyźnie, zwaną płaszczyzną padania; kąt odbicia jest równy kątowi padania; kąt padania alfa i kąt załamania beta spełniają następującą zależność:



(względny współczynnik załamania światła)
przy czym: V1 i V2 - wartości prędkości fali odpowiednio w ośrodkach 1 i w 2;
n = sin alfa / sin beta - współczynnik załamania ośrodka 2 względem1;

Bezwzględny współczynnik załamania światła

3)Bezwzględny współczynnik załamania światła dany jest wzorem 

v - prędkość światła w danym ośrodku
c - prędkość światła w próżni (c = 299 792 458 m/s)
n - bezwzględny współczynnik załamania

Znajomość bezwzględnych współczynników załamania umożliwia szybkie obliczenie prędkości światła w danych ośrodku, wg wzoru:

 

Odbicie całkowite wewnętrzne, odbicie światła zachodzące na granicy dwóch ośrodków przezroczystych charakteryzujących się współczynnikami załamania n₁ i n₂, n₁>n₂. Zjawisko obserwuje się w ośrodku o większym współczynniku załamania.

Polega ono na odbiciu światła zachodzącym bez strat energii, nie towarzyszy mu załamanie światła. Obserwuje się go, gdy kąt padania (tj. kąt zawarty pomiędzy normalną do powierzchni a kierunkiem promienia światła) jest większy od tzw. kąta granicznego całkowitego odbicia wewnętrznego. Wartość tego kąta wyraża się wzorem:

γ=arcsin(n₂/n₁).

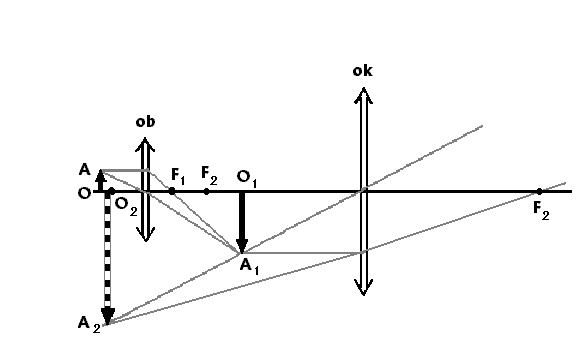
Mikroskop jest przyrządem optycznym służącym do zwiększenia kąta widzenia przedmiotów położonych w odległości dobrego widzenia oka. Składa się on z dwóch układów zbierających - obiektywu i okularu, w których do maksimum skompensowano wpływ wad soczewek (aberracji sferycznej i chromatycznej). Bieg promieni w mikroskopie przedstawiony jest na rys.1.

Rys.1. Bieg promieni w mikroskopie.

Przedmiot OA umieszczony jest w niewielkiej odległości za ogniskiem obiektywu. Obiektyw daje obraz powiększony, odwrócony i rzeczywisty - obraz O₁A₁ jest przedmiotem dla okularu i znajduje się między ogniskiem a okularem. Obraz, jaki daje okular jest pozorny, prosty, powiększony i znajduje się w odległości dobrego widzenia od okularu. Powiększenie mikroskopu jest iloczynem powiększenia obiektywu i okularu:

W = W₁ · W₂

Powiększenie obiektywu W₁ określone jest wzorem:

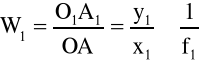
gdzie:

d - odległość dobrego widzenia

f₂ - ogniskowa okularu.

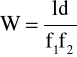
Zatem:

Od mikroskopu wymaga się, aby w obrazie oglądanego przedmiotu nawet najbliżej położone siebie punkty były rozróżnialne jako oddzielne. Wzór sugeruje, że powiększenie mikroskopu można zwiększać nieograniczenie - co byłoby zgodne z naszymi wymaganiami. Jednak w praktyce każdy mikroskop ma ograniczoną zdolność rozdzielczą. Przez zdolność rozdzielczą rozumiemy odwrotność najmniejszej odległości d pomiędzy dwoma punktami, które widzimy pod mikroskopem jako oddzielne. Ograniczona zdolność rozdzielcza wynika z falowej natury światła. Według teorii Abbego, preparat umieszczony pod mikroskopem można traktować jako siatkę dyfrakcyjną o stałej d. Siatka jest oświetlona wiązką równoległą, na jej szczelinach promienie zostają ugięte i po zebraniu ich przez obiektyw powstaje obraz szczeliny siatki w płaszczyźnie ogniskowej obiektywu (rys.2). Warunkiem powstania obrazu

Rys.2. Obserwacja obrazu siatki dyfrakcyjnej w mikroskopie.

szczeliny jest zebranie przez obiektyw dwóch promieni - pierwszego nieugiętego oraz ugiętego pierwszego rzędu. aby te promienie wzmacniały się przy spotkaniu w jednym punkcie, musi być spełnione znane równanie siatki:

gdzie:

λ - długość fali

d - stała siatki

φ₁ - kąt ugięcia promienia pierwszego rzędu w siatce dyfrakcyjnej.

--> [Author:KK]

Kąt φ nie może być większy od połowy kąta 2φ, pod jakim widziany jest obiektyw ze szczeliny siatki dyfrakcyjnej. Kąt 2φ nazywany jest kątem rozwartości mikroskopu (rys.3).

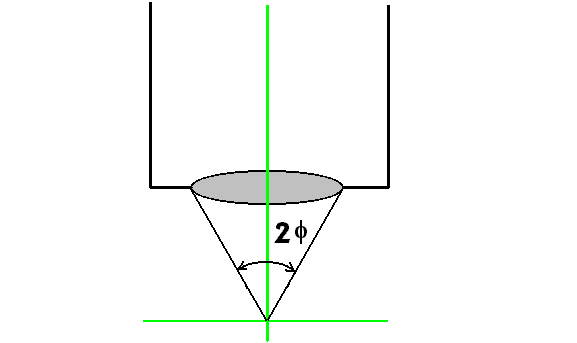
Rys.3. Apertura obiektywu.

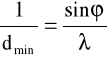
Równanie siatki określa zdolność rozdzielczą mikroskopu. Wynika z niego, że:

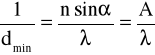
Jeżeli między obiektyw i obserwowany preparat wprowadzimy ośrodek (ciecz immersyjną) o współczynniku załamania n względem powietrza, równym współczynnikowi załamania szkła względem powietrza, wówczas zdolność rozdzielcza wzrasta - jest ona określona wzorem:

Wyrażenie A = n sin α nazywane jest aperturą numeryczną obiektywu.

Na granicy dwóch ośrodków światło ulega załamaniu. Prawo załamania mówi, że: promień padający, załamany oraz normalna do granicy dwóch ośrodków leżą w jednej płaszczyźnie, a współczynnik załamania n jest równy stosunkowi sinusów kąta padania α i załamania β. Jeżeli kąt jest mały, wtedy zachodzi: sin α ≈ tg α ≈ α i podobnie: sin β ≈ tg β ≈ β.

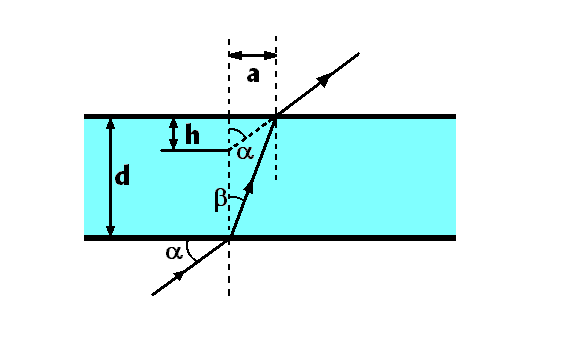
Rys.4. Bieg promienia w płytce płasko-równoległej

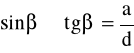
Korzystając z tych upraszczających założeń oraz opierając się na biegu promienia świetlnego w płytce płasko-równoległej (rys.4) możemy napisać:

oraz

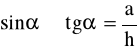
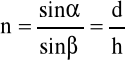
skąd

gdzie:

d - grubość rzeczywista płytki szklanej

h - grubość pozorna.

W celu wyznaczenia współczynnika załamania płytki szklanej należy:

1. Przy pomocy śruby mikrometrycznej zmierzyć grubość rzeczywistą d. Pomiar przeprowadzić trzykrotnie - wyniki wpisać do tabeli 2.

---