KRATOWNICE - Przykłady prostych konstrukcji i ich obliczanie
PRZYKŁAD I
Określić, które pręty kratownicy służącej do podwieszenia rur instalacji chemicznej są rozciągane, a które ściskane.
Określić siły występujące w prętach kratownicy, jeśli całkowity ciężar rur wynosi 3.8 [kN/m].
ROZWIĄZANIE
ad. 1) Patrz odpowiedź do zadania
ad. 2)
Całkowite obciążenie na jedną kratownicę:
![]()
Obciążenie jednego węzła
![]()
Uwzględniając ciężar kratownicy przyjmiemy ostatecznie obciążenie w węźle
![]()
Schemat statyczny kratownicy
Warunek statycznej (wewnętrznej) wyznaczalności:
![]()
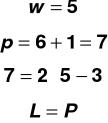
Warunek równowagi węzła E
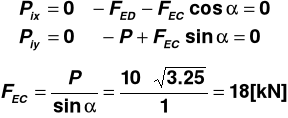
- pręt rozciągany
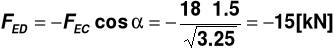
- pręt ściskany
Warunek równowagi węzła D
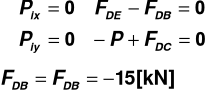
- pręt ściskany
![]()
- pręt rozciągany
Warunek równowagi węzła C
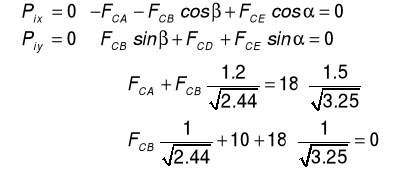
![]()
- pręt ściskany
![]()
- pręt rozciągany
METODA RITTERA
Równania równowagi
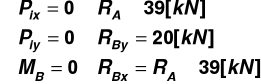
Przecięcie przez trzy pręty nie przechodzące przez jeden punkt
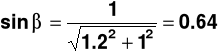
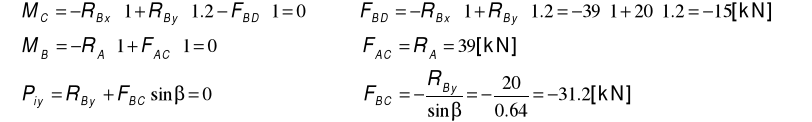
ODPOWIEDŹ DO ZADANIA 1.
(siły w kN)
PRZYKŁAD II
Wyznaczyć siły w prętach kratownicy przenoszącej obciążenie kładką o rozpiętości L=12[m]. Każdy pręt - oprócz poprzecznych wzmocnień - ma długość l=3[m]. Kładka ma szerokość b=2[m], a jej ciężar wynosi G=35[kN]. Wartość charakterystyczna obciążenia zmiennego Q=4 [kN/m2]. Częściowy współczynnik bezpieczeństwa obciążenia statycznego ![]()
, a obciążenia dynamicznego ![]()
ROZWIĄZANIE
Obciążenie stałe przypadające na 1 metr mostu
![]()
Każdy węzeł dolnego pasa dwóch kratownic (lewej i prawej) obciążony jest 3 metrami kładki
![]()
Na jedną kratownice przypada
![]()
Obciążenie zmienne pochodzi z części kładki o szerokości b=2[m] i długości l=3[m]. Na jeden węzeł przypada więc
![]()
Ostatecznie obciążenie węzła wynosi
![]()
Schemat statyczny kratownicy
Metoda Rittera (rozwiązanie dla prętów DF, DE i CE)
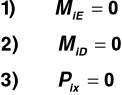
ad. 1) ![]()
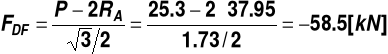
pręt ściskany
ad. 2) ![]()
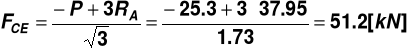
pręt rozciągany
ad. 3) ![]()
![]()
pręt rozciągany
PRZYKŁAD III
Zbiornik wodny umieszczony jest na kratownicy przestrzennej. Znaleźć siły występujące w dolnych prętach kratownicy: AC, BC i CD wywołanych jedynie siłą wiatru ![]()
. Częściowy współcznnik bezpieczeństwa wynosi ![]()
ROZWIĄZANIE
Powierzchnia zbiornika -
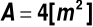
Obciążenie charakterystyczne wiatrem -
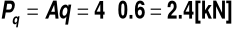
Obciążenie obliczeniowe na dwie kratownice boczne -
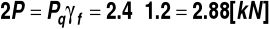
. Ostatecznie:
Schemat statyczny
Przekrój 1° Przekrój 2°
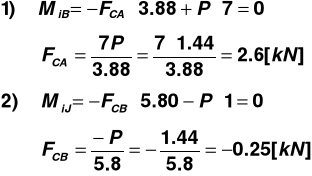

A
B
C
D
E
P
P
1.2[m]
1.5[m]
1.0[m]
FED
FEC
E
P=10[kN]
P=10[kN]
FDB
D
FDC
FDE = -15[kN]
FCD = 10[kN]
FCA
C
FCB
FCE = 18 [kN]
α
β
1.0[m]
1.5[m]
1.2[m]
P
P
E
D
C
B
A
RA
RBx
RBy
RBy
RBx
RA
α
B
A
FAC
FBC
FBD
C
B
β
RBy=20
RBx=39
RA=39
P
39.0
15.0
P=10
P=10
E
D
P=10
B
A
31.2
10.0
18.0
15.0
P
P
RJ=37.95[kN]
RA=37.95[kN]
A
B
G
C
E
F
D
H
D
C
B
A
P
E
FDE
FCE
FDF
RA
A
B
G
F
E
D
C
H
1m
2m
2m
2m
2m
2m
2m
2m
4m
WIATR
PRZEKRÓJ 2°
PRZEKRÓJ 1°
3.88m
5.8m
FCA
FCB
FDB
FEC
FDC
FDB
P=1.44[kN]
P=1.44[kN]
E
B
J
J
C
D
y
5 m
5 m
5 m
DESKI
POPRZECZNA BELKA
4 x l = 3 m
USZTYWNIENIE POPRZECZNE
b = 2 m
x
Wyszukiwarka
Podobne podstrony:
Przyklady - Wyklad 1, Studia - Materiały, Badania Operacyjne, Zemke
Laborki 2, Studia, Wytrzymałość materiałów II, Test z laborek wydymalka, lab
L4 - pytania, Studia, Wytrzymałość materiałów II, lab4 wm2 studek
Doc1, budownictwo studia, wytrzymałość materiałów, Книга Обсл і рем
Spec. tech.(Skw.+Międz. ) poprawiona, budownictwo studia, wytrzymałość materiałów, Книга Обсл і рем
ZMIST, budownictwo studia, wytrzymałość materiałów, Книга Обсл і рем
Laborki 2, Studia, Wytrzymałość materiałów II, Test z laborek wydymalka, lab
Rownowaga cial sztywnych Teoria - przykłady obliczeń, Prywatne, Wytrzymałość materiałow
Zginanie prętów silnie zakrzywionych, Studia, Wytrzymałość materiałów
Badanie twardości, budownictwo studia, wytrzymałość materiałów
Metody energetyczne, Studia, Wytrzymałość materiałów
stal 1, budownictwo studia, wytrzymałość materiałów
wytrzymałośc teoria, Politechnika Lubelska, Studia, Studia, Wytrzymałośc materiałów
Ugięcie ramy 1-sprawozdanie, Studia, wytrzymałość materiałów
Laborki 1, Studia, Wytrzymałość materiałów II, Test z laborek wydymalka, lab
Kratownice przyklady z wykladu
więcej podobnych podstron