Sprawozdanie pobrane ze StudentSite.pl
Chcesz więcej? Wejdź na: http://www.studentsite.pl/materialy_studenckie.html
Możesz także wspomóc swoimi sprawozdaniami innych: http://www.studentsite.pl/panel_materialy_studenckie/add

2FA

17.03.2010

Laboratorium z fizyki

Ćw. nr: 1

Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego

Tomasz Sapyta

L 3

WSTĘP

Celem ćwiczenia jest wyznaczenie przyspieszenia grawitacyjnego za pomocą wahadła matematycznego i rewersyjnego. W obydwu przypadkach mamy do czynienia z ruchem harmonicznym prostym czyli takim, w którym siła wprawiająca w ruch jest proporcjonalna do wychylenia i przeciwnie skierowana do prędkości. Wahadłem matematycznym nazywamy punkt materialny zawieszony na nieważkiej i nierozciągliwej nici, wykonujący wahania wokół położenia równowagi (rysunek). Wahadło rewersyjne jest natomiast szczególnym przypadkiem wahadła fizycznego (ciało materialne zawieszone na osi i wykonujące wahania wokół położenia równowagi). Składa się ono z metalowego pręta, na którym osadzone są w kolejności : soczewka metalowa M1, ostrze O, soczewka metalowa M2 oraz ostrze O' (ostrza zwrócone są ku sobie) (rysunek). Zarówno ostrza, jak i soczewki można przesuwać wzdłuż pręta. Położenie soczewek można dobrać tak, by okresy oscylacji wokół osi przechodzących przez te soczewki były sobie równe. Zarówno dla wahadła matematycznego jak i fizycznego okres drgań (dla niedużych wychyleń) zależy tylko od długości wahadła i przyspieszenia ziemskiego, nie zależy zaś od wychylenia. Dla wahadła matematycznego wyraża się on wzorem : gdzie : l - długość wahadła; g - przyspieszenie ziemskie. Po prostych przekształceniach otrzymujemy wzór pozwalający obliczyć szukane przyspieszenie ziemskie: . Natomiast dla wahadła fizycznego okres oscylacji ogólnie wyraża się wzorem : gdzie :

Wahadło rewersyjne (z lewej strony) i wahadło matematyczne (z prawej strony)

I_S - moment bezwładności wahadła gdy oś obrotu przechodzi przez środek ciężkości; m. - masa wahadła; d - odległość osi obrotu od środka ciężkości. Wprowadzając do powyższego wzoru oznaczenie wyrazimy okres wahadła fizycznego wzorem skąd po prostych przekształceniach otrzymujemy wzór na przyspieszenie ziemskie . Wielkość l' nazywamy długością zredukowaną wahadła fizycznego. Geometrycznie jest to odległość między ostrzami wahadła rewersyjnego, gdy okresy dla osi obrotu przechodzącej przez punkt O (T) i O' (T') są sobie równe. Gdybyśmy zbudowali wahadło matematyczne o długości l' to miałoby ono okres równy okresowi wahadła fizycznego spełniającego warunek .

PRZEBIEG ĆWICZENIA

1. Zawiesić wahadło rewersyjne na ostrzu B i ustawić masę m₂ w pobliżu ostrza A.

2. Wprawić wahadło w ruch (wychylenie
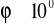
   dla każdego wzbudzenia takie samo) i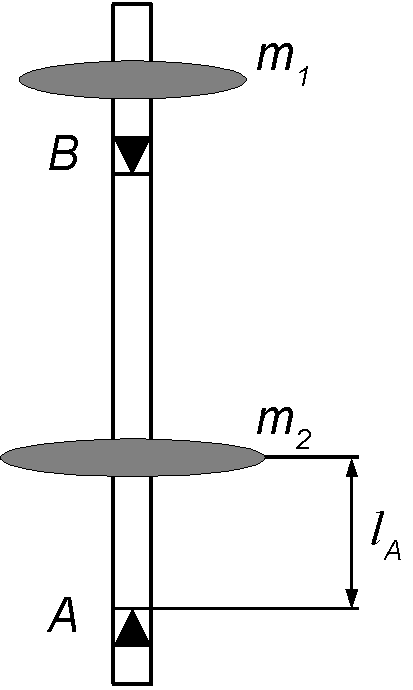
   zmierzyć za pomocą sekundomierza czas t dziesięciu wahnięć i wyliczyć wartość okresu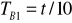
   .

3. Następnie odwrócić wahadło i zawiesić je na ostrzu A i podobnie jak punkcie 2 wyznaczyć wartość okresu
   .

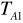
4. Przesunąć masę m₂ o 5 cm w stronę B i ponownie wyznaczyć okres drgań
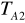
   dla zawieszenia A.

5. Wahadło odwrócić, zawiesić na ostrzu B i zmierzyć T_B2.

6. Powtórzyć pomiary wg. punktów 4,5 i znaleźć dwa szeregi wartości okresów T_A1, T_A2, ...T_An i T_B1, T_B2, ... T_Bn dla wszystkich możliwych położeń masy m₂ pomiędzy zawieszeniami A i B w odstępach co 5 cm. Wyniki zapisać w tabeli.

Tabela z pomiarami:

l_An

t_An

t_Bn

T_An

T_Bn

L_r

T

g

m

s

s

s

s

m

s

m/s²

0,1

 

23,29

 

2,329

1,3

2,275

9,906 ± 0,1

0,15

22,52

22,83

2,252

2,283

0,2

22,4

22,41

2,24

2,241

0,25

22,28

21,92

2,228

2,192

0,3

22,12

21,56

2,212

2,156

0,35

22,06

21,34

2,206

2,134

0,4

21,86

21,06

2,186

2,106

0,45

21,68

20,78

2,168

2,078

0,5

21,5

20,55

2,15

2,055

0,55

21,43

20,13

2,143

2,013

0,6

21,14

19,92

2,114

1,992

0,65

20,87

19,84

2,087

1,984

0,7

20,82

19,89

2,082

1,989

0,75

20,89

20,12

2,089

2,012

0,8

21,06

20,41

2,106

2,041

0,85

21,4

20,85

2,14

2,085

0,9

21,78

21,15

2,178

2,115

0,95

21,94

21,62

2,194

2,162

1

22,16

21,9

2,216

2,19

1,05

22,41

22,27

2,241

2,227

1,1

22,69

22,72

2,269

2,272

1,15

23,03

22,94

2,303

2,294

1,2

23,34

2,334

1,25

23,71

2,371

1,3

23,99

2,399

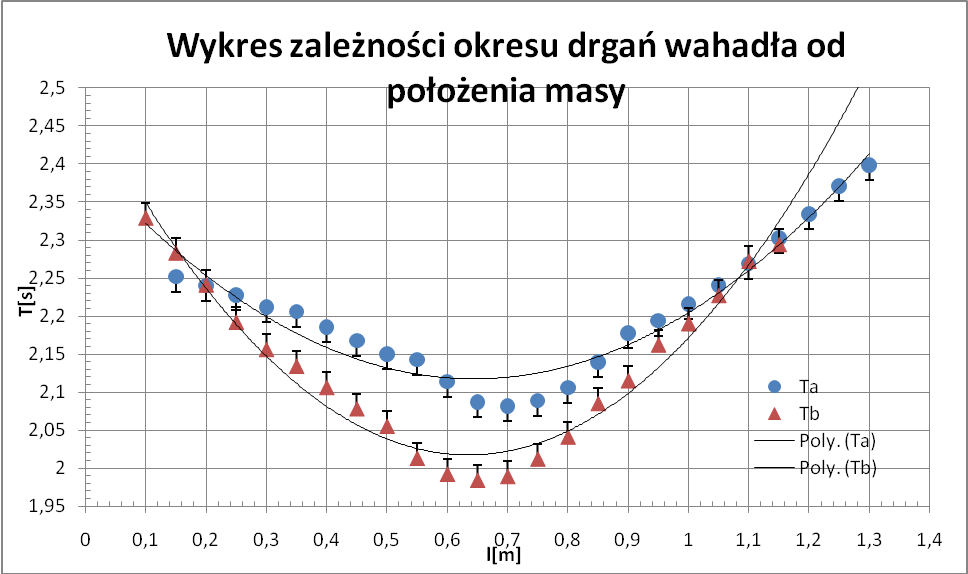
Obliczenia :

1. Niepewnośc standardowa dla l_A:

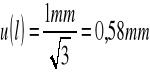
2. Niepewność standardowa dla t:

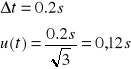
3. Niepewność DT:

4. Wartość okresu T

T_AB1=2,29 s

T_AB2=2.26s

5. Przyśpieszenie ziemskiego

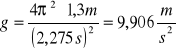
6. Niepewność pomiaru przyśpieszenia ziemskiego

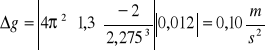
gdosw [m/s^2]	gteor [m/s^2]	Δ[%]
9,906	9,81	9,6

Wnioski:

Otrzymane przez nas wyniki w nieznacznym stopniu odbiegają od wartości tablicowej która wynosi 9,906 . Może to być spowodowane przez to, drgania wykonywane przez wahadła były w rzeczywistości hamowane wskutek oporu powietrza czy też tarcia wahadła rewersyjnego o zawieszenie. Błędy mogły się także pojawić podczas pomiarów odległości i mierzonych czasów.

4

---