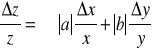PREZENTACJA WYNIKÓW POMIARÓW Pomiary są wykonywane tylko z pewnym stopniem dokładności. To ograniczenie wynika z: - niedoskonałości przyrządów użytych podczas pomiaru - skończonej precyzji narządów zmysłów obserwatora.
Nawet najbardziej precyzyjnie wykonany pomiar x obarczony jest niepewnością pomiarową i stanowi przybliżenie wartości rzeczywistej x .	Nie znamy wartości rzeczywistej x , lecz mamy pewność, że mieści się ona pomiędzy x- x< x <x+ x
Jedynym sensownym sposobem zapisu wartości x wielkości mierzonej jest: (wartość wielkości mierzonej ± niepewność pomiarowa) jednostka	W wyniku pomiaru powinna być zapisana jego wartość, niepewność pomiarowa i jednostka: D = (36,43 ± 0,25 ) cm = (36,43 ± 0,25 )x10^-2 m
Wynikiem pomiaru jest przedział liczbowy, a nie jedna wartość

Czynniki, które wpływają na pomiary dzielimy na dwie grupy: błędy pomiarowe - likwidujemy usuwając ich źródła lub wprowadzając odpowiednie poprawki. NIEPEWNOŚCI pomiarowe - związane głównie z ograniczeniami aparatury i niedoskonałością obserwatora, można je zmniejszyć poprzez zastosowanie dokładniejszej aparatury lub lepszego sposobu mierzenia; nie można ich całkowicie wyeliminować
niepewność x - wynika ze skończonego odstępu sąsiednich kresek podziałki na skali przyrządu np. przy skali milimetrowej x. = 1mm.	W przypadkach, kiedy odstępy pomiędzy kolejnymi kreskami podziałki są duże, można przyjąć, że x jest równa ½ lub nawet ¼ najmniejszej działki
niepewność x - dokładność wzorcowania fabrycznego przyrządu czyli klasa przyrządu zdefiniowana : x = ( )	Oznacza to, że dla miernika klasy k=1.5 o zakresie do 2A x=0.03 A . Ta wartość jest stała dla całego zakresu pomiarowego i stąd zaleca się taki wybór zakresu miernika analogowego (wskazówkowego), aby mierzona wartość była większa niż połowa zakresu (wtedy niepewność względna jest mniejsza).
maksymalna niepewność jest równa: xs = x + x W każdym doświadczeniu należy wstępnie oszacować wielkość poszczególnych niepewności i te, które są małe w porównaniu z innymi można zaniedbać.

Wynik pomiarów (bezpośredni lub będący wynikiem obliczeń, jeśli wyznaczamy wielkość złożoną np, objętość prostopadłościanu na podstawie pomiarów jego krawędzi) podajemy wraz z NIEPEWNOŚCIĄ BEZWZGLĘDNĄ I WZGLĘDNĄ.
Bezwzględna niepewność pomiarowa x określa, o ile wynik pomiaru x może różnić się od rzeczywistej wartości x0:	wynik końcowy zapisujemy w postaci
Niepewność względną określamy jako stosunek niepewności bezwzględnej do wartości otrzymanego wyniku (może być stosunek niepewności pomiarowej wyniku do wartości średniej wyniku) i wyrażamy ją zazwyczaj w procentach	% określa precyzję pomiaru, najmniejszą niepewnością są obarczone pomiary z końca przedziału
Niepewność pomiarowa może być standardowa bądź maksymalna
STANDARDOWA	połowa długości przedziału, w którym mieści się około 2/3 wyników
MAKSYMALNA	połowa długości przedziału, w którym mieszczą się wszystkie wyniki
SERIA POMIARÓW TEMPERATURY WODY

NIEPEWNOŚCI W POMIARACH BEZPOŚREDNICH
wielkością najbardziej prawdopodobną (najbardziej zbliżoną do wartości rzeczywistej) dla skończonej liczby pomiarów jest ich średnia arytmetyczna
NIEPEWNOŚCI WIELKOŚCI ZŁOŻONYCH (uzyskanych z pomiarów pośrednich )
Najczęściej wyznaczamy wielkości fizyczne, których nie można zmierzyć w sposób bezpośredni za pomocą przyrządów, ale znany jest przepis funkcyjny z= wiążący wielkość z (pomiar pośredni) z innymi wielkościami x1, x2,...xn mierzonymi bezpośrednio	objętość sześcianu wyznaczamy mierząc długość jego krawędzi V(x,y,z), przyspieszenie ziemskie g wyznaczamy mierząc okres T i długość i wahadła g (T,l), ogniskową soczewki możemy wyznaczyć mierząc odległość przedmiotu i obrazu od soczewki f(x,y)
Elementarna metoda obliczania niepewności przykład: v=s/t v = , v =	z= niepewność maksymalna wynik pomiaru z równy średniej arytmetycznej z=
niepewność pomiarowa wielkości złożonych Sumy Różnicy Iloczynu Ilorazu gdzie: a, b, c - wielkości mierzone bezpośrednio; s - liczba w przypadkach gdy z= Ax y ; nawias zawiera sumę wyrazów dodatnich, z których każdy przedstawia wkład błędu pomiaru danej wielkości w błąd wyniku końcowego	maksymalny błąd względny,

OPRACOWANIE WYNIKÓW METODĄ GRAFICZNĄ
W przypadku opracowania wyników pomiarów wielkości zależnych, gdy y = f(x), stosujemy metodę graficzną czyli wykonujemy wykresy. Osie układu powinny być opisane, tzn. podane wielkości, które odkładamy na osiach oraz ich jednostki Odpowiednio dobrana skala tak, by na osi znajdował się cały przedział zmienności wielkości fizycznej ( oznacza to, że podziałka nie musi zaczynać się od zera ) oraz można było łatwo odczytać współrzędne punktów Należy zaznaczyć punkty pomiarowe oraz niepewności pomiarowe (punkt pomiarowy znajduje się w prostokącie niepewności pomiarowych). Jeśli tylko jedna wielkość jest obarczona niepewnością, np. zmienna zależna Y, to zaznaczamy to pionową kreską o długości 2y, której środek przypada w danym punkcie. W przypadku, gdy obie zmienne obarczone są niepewnościami pomiarowymi, zaznaczamy to w postaci krzyżyka o ramionach 2x i 2y, na przecięciu których znajduje się punkt reprezentujący dany pomiar Wykreślona krzywa powinna przechodzić przez wszystkie prostokąty niepewności. Nie łączymy punktów łamaną! Punkty wytyczające krzywą nie muszą na niej leżeć, a powinny być raczej równomiernie rozmieszczone powyżej i poniżej krzywej. Należy jednak dbać o to, by krzywa mieściła się w granicach zaznaczonych niepewności pomiarowych
ANALIZA ZALEŻNOŚCI LINIOWYCH
Bardzo często mierzone wielkości fizyczne x i y związane są zależnością liniową: y= ax + b Współczynnik a odpowiada za nachylenie prostej, a współczynnik b za punkt przecięcia z osią rzędnych. Zazwyczaj współczynniki a i b mają interpretację fizyczną (są wyrażone w odpowiednich jednostkach) i ich znajomość pozwala wyznaczyć niektóre wielkości fizyczne.	w przypadku zależności liniowej (lub po linearyzacji) należy rozważyć (wykreślić) proste o skrajnych współczynnikach kierunkowych (poprowadzone przez skraje prostokątów niepewności pomiarowych pomiarów bezpośrednich) Jako rzeczywiste nachylenie przyjmuje się średnią arytmetyczną a= , a błąd maksymalny nachylenia:
Linearyzacja to przekształcanie związków nieliniowych w związki liniowe (w funkcje typu Y (X) = AX + B).
Przykłady linearyzacji
Ruch jednostajnie przyspieszony bez prędkości początkowej Droga w tym ruchu wyraża się wzorem s = ½at^2. Jest to przykład funkcji kwadratowej, jej wykresem jest dodatnia gałąź paraboli. Transformacja tego związku na zależność liniową Y = AX + B: Y = s A = ½a X = t^2 B = 0	Okres wahadła matematycznego wyraża się wzorem: Wprowadzamy nowe zmienne , wtedy Y(X)=AX+B, gdzie A= zaś B w granicach błędu powinno byćB=0

PRZYBLIŻENIA
Końcowe rezultaty należy podawać we właściwie dobranych jednostkach i z odpowiednią precyzją. O precyzji zapisu danej liczby świadczy ilość zawartych w niej CYFR ZNACZĄCYCH.
Cyframi znaczącymi są cyfry od 1 do 9		np. liczba 321 ma 3 cyfry znaczące (lub miejsca znaczące).
Zero jest cyfrą znaczącą tylko w przypadku, gdy znajduje się między dwiema cyframi nie będącymi zerami, albo na dowolnym miejscu po cyfrze nie będącej zerem, ale zawartej w liczbie z przecinkiem.		np. liczbę 500 możemy zapisać jako 5 10^2, przedstawia więc ona jedno miejsce znaczące; jeśli chcemy zaznaczyć, że posiada ona trzy cyfry znaczące, należy przedstawić ją w postaci 5,00 10^2. Zer będących miejscami znaczącymi nie należy opuszczać.
W ułamkach dziesiętnych ilość miejsc znaczących odpowiada ilości cyfr po ostatnim zerze, przed którym nie ma cyfr znaczących		np. liczba 0,00120 ma 3 miejsca znaczące
Ułamki dziesiętne wygodnie jest zapisywać w postaci liczby nie będącej zerem, mnożonej przez 10 w odpowiedniej potędze		np. 0,00120 = 1,20 10^-3
Teoretycznie wyniki mogą być obliczane do dowolnego miejsca rozwinięcia dziesiętnego, ale sens fizyczny mają najwyżej dwie cyfry znaczące niepewności.
Zaokrąglanie zaczynamy od niepewności pomiarowej:	Obliczamy niepewność pomiarową z trzema cyframi znaczącymi x,y,z, co można zapisać w postaci gdzie , m należy do zbioru liczb całkowitych i jest tak dobrane, aby x znajdowało się na pierwszym miejscu po przecinku.
Niepewność pomiarową zaokrąglamy do dwóch miejsc znaczących (Międzynarodowa Norma Oceny Niepewności Pomiaru)	i to tylko wtedy, gdy pierwszą cyfrą znaczącą jest 1 lub 2. W pozostałych przypadkach wynik obliczeń zaokrąglamy do jednej cyfry znaczącej. Wiąże się to z faktem, że nie jesteśmy z reguły w stanie wyznaczyć niepewności pomiarowej z dokładnością lepszą niż około 20% jej wartości
Obowiązuje zasada, że wynik pomiaru zaokrąglamy do tego samego miejsca rozwinięcia dziesiętnego co niepewność	Wyniki obliczeń zaokrąglamy w ten sposób, że ostatnia cyfra, która została po opuszczeniu cyfr końcowych nie ulega zmianie, jeżeli następują po niej cyfry od 0 do 4 oraz ostatnią cyfrę zwiększamy o 1, jeśli następują po niej cyfry od 5 do 9
Z podanych powyżej zasad wynika, że powinniśmy dokonywać obliczeń z dokładnością o co najmniej jedno miejsce znaczące większą, niż dokładność z jaką podajemy wynik końcowy.
przykładów poprawnego zapisywania wyników końcowych: m = (92,34 +/- 0,12)10^-3 kg, mwzgl.= 0,13%, I = (12,7 +/- 0,8) mA, Iwzgl.= 6%, C = (30,00 +/- 0,11) nF, Cwzgl.= 0,4%, T = (293 +/- 1) K, Twzgl.= 0,3%, h = (6,59 +/- 0,25)10-34 J s, hwzgl.= 4%.

RUCH JEDNOSTAJNIE PRZYSPIESZONY BEZ PRĘDKOŚCI POCZĄTKOWEJ_1

Droga s (m)	Czas t (s)			tśr (s)	t^2 (s^2)
0,10	0,9	0,9	1,0	0,9	0,8
0,20	1,5	1,5	1,4
0,30	1,9	1,9	1,6
0,40	2,3	2,0	2,3
0,50	2,3	2,7	2,6
0,60	3,0	2,4	2,7
0,70	3,2	3,0	2,8
0,80	3,3	3,3	3,0
0,90	3,4	3,4	3,4

lp	a	a/a *)	a=a*( a/a)	wynik
1
2
3
4
5
6
7
8
9	0,158	0,12	0,019 m/s^2	a= (0,158 +/- 0,019) m/s^2

METODA GRAFICZNA

1. linearyzacja zależności s(t), czyli s(t²)=
   

• niepewność
  (t²) jest niepewnością pomiaru złożonego,

• 
  stąd
  (t²)=2(
  t) *t

Droga s (m)	s	tśr (s)	t (s)	(t^2 ) (s^2)
0,10	0,05 m	0,9	0,2	0,4
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90

METODA GRAFICZNA NAJMNIEJ / NAJBARDZIEJ KORZYSTNEGO PRZYPADKU

• prowadzimy proste przez prostokąty niepewności pomiarowych tak, aby uzyskać prostą o największym nachyleniu (odpowiada to a_max) oraz najmniejszemu - a_min )

• obie proste powinny przecinać się w okolicach środka wykresu

• obliczamy średnie przyspieszenie a _śr = ( a_max + a_min )/2

• oraz niepewność
  a= ( a_max - a_min )

• a = a _śr
  
  a

WYZNACZ PRZYSPIESZENIE na podstawie pomiarów czasu i drogi w ruchu jednostajnie przyspieszonym (bez prędkości początkowej) _2
wiedząc, że niepewności pomiarów czasu i drogi wynosiły odpowiednio:

t =0,05 s;
s =0,01 m

PRZYKŁADY POMIARÓW

Przykład 1

Uczeń przebiegł dystans s=(100,0
0,5)m w czasie t= (12,5
0,2)s. Jaka była jego średnia prędkość?

Przykład 2

Wykonano pomiar przyspieszenia ziemskiego pomocą wahadła matematycznego otrzymując następujące wyniki pomiarów bezpośrednich: l=
, T=

Przykład 3

Wykonano pomiar wytrzymałości tafli lodowej i stwierdzono, że załamała się ona po położeniu na niej kolejno 6 cegieł o ciężarach: P
=25N, P2=30 N, P3=28 N, P4=24 N, P5=26N. Jaka była wytrzymałość W lodu, jeśli niepewność pomiarów ciężarów cegieł była jednakowa i wynosiła
P=1N?

Przykład 4

Obliczyć gęstość
cylindra, którego objętość wyznaczono jako V=
(również jako niepewność wielkości złożonej), jeśli jego masa wynosiła m=

WYNIKI POMIARÓW

Zaokrąglanie wyników

• przed zaokrągleniem należy obliczyć maksymalna niepewność pomiarową (różniczka zupełna)

• niepewności pomiarowe zaokrągla się tylko w górę i do pierwszej cyfry znaczącej różnej od zera (chyba, że zaokrąglenie daje znaczny wzrost niepewności, wtedy do dwóch cyfr)

Cyfry powtarzające się w serii pomiarów są pewne, a zmieniające się (np. na którymś miejscu po przecinku) - są wątpliwe.

Przy obliczaniu średniej x pomiarów zachowuje się tylko jedną cyfrę wątpliwą.

1. Jeśli wynik jakiegoś pomiaru pośredniego jest sumą lub różnicą wyników kilku pomiarów, to ma on co najmniej ten rząd jednostek wątpliwy, jaki jest wątpliwy w tym składniku, w którym jest on najwyższy.(dziesiętne są jednostkami wyższego rzędu, niż setne itp.)

6,83+25,327+7,4 - 23,64 (= 15,917) = 15,9 bo 4 jest najwyższym rzędem cyfry wątpliwej

2. Jeśli wynik jakiegoś pomiaru pośredniego jest iloczynem lub ilorazem wyników kilku pomiarów, to ma on najwyżej tyle miejsc pewnych (licząc cyfry od lewej, ku prawej) ile miejsc pewnych ma ten x czynników, który ma ich najmniej.

55,36 * 44,7 = 2474,592 = 2,47 * 10
cyfra 7 jest wątpliwa, tzn. że wątpliwe są dziesiątki

3. przy podnoszeniu liczby przybliżonej do kwadratu lub trzeciej potęgi należy w wyniku zachować o jedno miejsce znaczące mniej, niż miała ich liczba podnoszona do potęgi, np.

2,44
(=5,954)=6,0

36,5
(=1332,3)=1330

8,57
(=629,4)=630

0,995
(=0,9851)=0,98

INDEKS, Nowa matura z fizyki na poziomie rozszerzonym

Dodatek 2: niepewności pomiarowe

1

8

2. Niepewności pomiarów bezpośrednich:
   s=0,5 cm (najmniejsza podziałka),
   t=(0,1+0,1)s (stoper + czas reakcji)

3. Wykres s(t) - czy to jest parabola?

4. Niepewność wielkości złożonej
   :
   *)

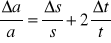
• Średnią wartość przyspieszenia oblicz jako średnią arytmetyczną wartości przyspieszeń

• Niepewność pomiaru średniej wartości przyspieszenia oblicz jako wartość bezwzględną największej różnicy średniej wartości przyspieszenia i wartości przyspieszenia dla danej chwili czasu

• przez prostokąty niepewności prowadzimy prostą (wystarczy, że będzie przechodziła przez 70% punktów)

• ponieważ interpretacją fizyczną współczynnika kierunkowego prostej jest: tg
  =
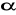
  , wyznaczamy tg
  z dowolnej pary punktów prostej, najlepiej z końca wykresu, bo tam niepewność względna jest najmniejsza

• wtedy szukane przyspieszenie a=2 tg
  

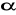
t,s	s,m
0	0,00
1	0,10
1,3	0,20
1,7	0,30
2	0,40
2,2	0,50
2,4	0,60
2,6	0,70
2,8	0,80
3	0,90

B różniczkowa metoda

obliczania niepewności pomiarów pośrednich

gdzie x=Ax
x

A elementarna metoda

obliczania niepewności pomiarów pośrednich

,

, zaś wynik pomiaru

wynik końcowy x' można obliczyć wprost ze wzoru, przy czym zazwyczaj nie zachodzi równość x=x'. Różnica
, w praktyce wystarczy by

Metoda A:
,

,

niepewność maksymalna

niepewność względna N=

Metoda B:

v=1*s/t=
, A=1, a=1, b=-1

Ze wzoru v=

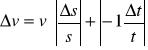
podstawiając liczby: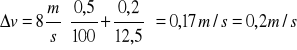

v=

Metoda B:

g=
10,05 m/s^2

g=
, A=
, a=1, b=-2

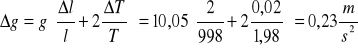
g=
, N=2,3%

Metoda A:

N=

Metoda B:

W= P1+P2+P3+P4+P5=133 N

Wynik końcowy: W=
, N=3,8%

Metoda A:

W
= (26+31+29+25+27) N

W
=(24+29+27+23+25)N

Wytrzymałość W=
=133 N

Maksymalna niepewność
=5N

Niepewność względna N=

Wynik końcowy:

W=
, N=3,8%

---