1. Zasada pomiaru

Licznik Geigera-Millera zbudowany jest z cylindrycznej katody i przeciągniętej wzdłuż jej osi metalowej nici stanowiącej anodę, umieszczonych w zamkniętym naczyniu wypełnionym gazem. Między anodę i katodę przyłożone jest wysokie napięcie, które przyspiesza elektrony powstałe w wyniku jonizacji gazu spowodowanej promieniowaniem jądrowym przechodzącym przez licznik. Przyspieszone elektrony powodują dalszą, lawinową jonizację.

Podczas gdy do anody tłumnie podążają elektrony, w gazie po jonizacji pozostają ospałe jony dodatnie, które - znacznie cięższe, poruszają się wolniej, ale konsekwentnie w myśl zasady Ciche jony brzegi rwą, tworząc ładunek przestrzenny w gazie, zmniejszający napięcie między anodą i katodą, a tym samym mimochodem powodujący zanik wyładowań lawinowych. Jednak po dojściu do katody jony dodatnie z całą stanowczością wybijają z niej elektrony i znowu rusza lawina.

Aby powstrzymać wyładowania ciągłe w liczniku, które niechybnie spowodowałyby nieczułość licznika na następne cząstki, włącza się w obwód licznika duży opór rzędu 109 omów, nie pozwalający na szybkie odprowadzenie ładunku ujemnego z anody, tym samym obniżający jej potencjał do chwili zebrania jonów dodatnich na katodzie i powodujący wygaśnięcie wyładowań lawinowych.

Po czasie rzędu 0,1 s - czasie martwym licznika - ładunek z anody zostaje odprowadzony, a licznik pali się do zarejestrowania nastepnej cząstki.

Celem doświadczenia jest wyznaczenie charakterystyki licznika, określenie napięcia progowego, obszaru występowania plateau i jego nachylenia.

2. Układ pomiarowy

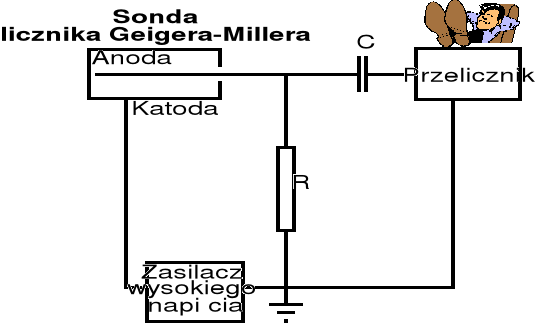
3. Ocena dokładności pojedynczych pomiarów

regulacja napięcia - przy zasilaczu wysokiego napięcia - co 1V

licznik impulsów - z wyświetlaczem cyfrowym, zmiana ostatniej cyfry - 1

4a. Tabela wyników

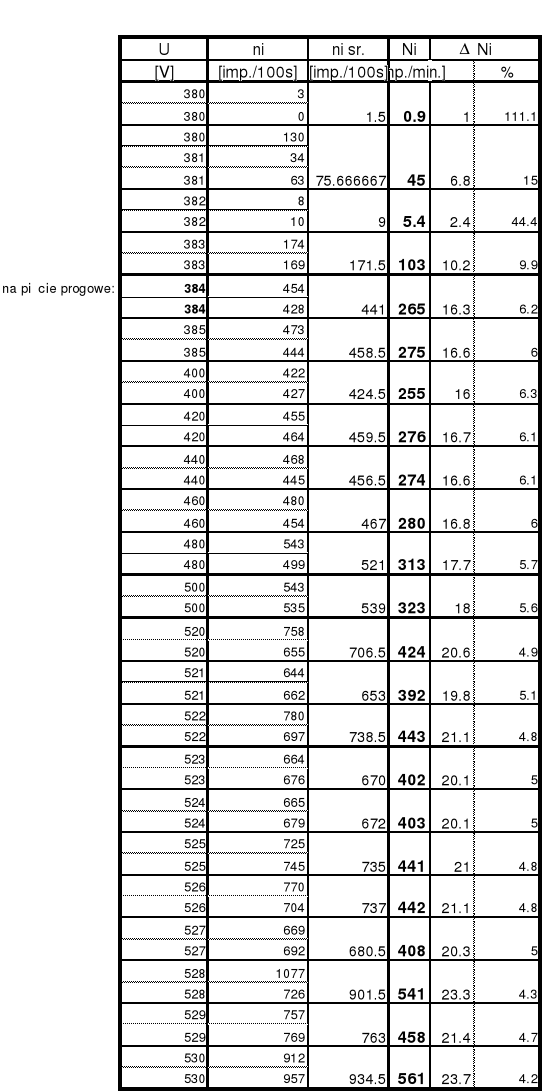
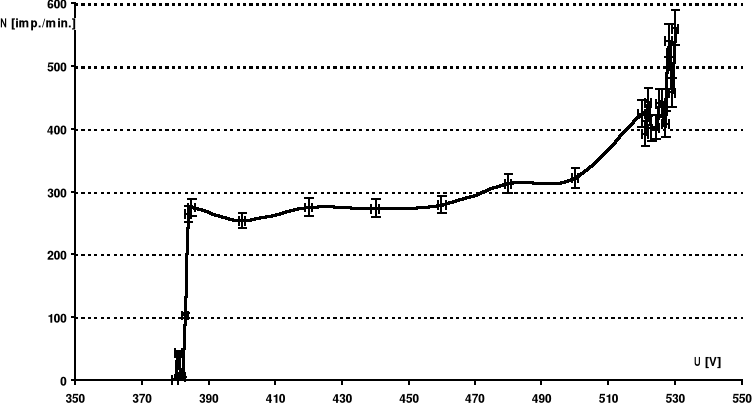
4b. Wykres charakterystyki licznika Geigera-Millera

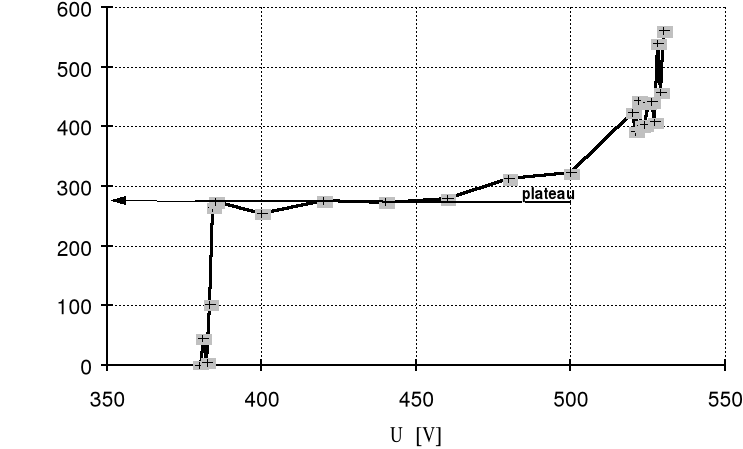
Na wykresie widać dokładnie trzy obszary charakterystyki. W obszarze niskich napięć licznik rejestruje jedynie cząstki o najwyższej energii, w obszarze środkowym - plateau - wszystkie przeszywające go cząstki, natomiast w zakresie wysokich napięć liczniik rejestruje każdą cząstkę dwu- i więcej- krotnie. Do wiarygodnych pomiarów nadaje się więc jedynie obszar o tyle wdzięcznej, co obco brzmiącej nazwie plateau.

Z wykresu można odczytać długość plateau i odpowiadający mu przyrost zliczeń N
oraz liczbę zliczeń Np dla środka plateau. W naszym wypadku wielkości te wynoszą odpowiednio:

N= 58.8

U= 116V

Np= 275

Z tych danych można obliczyć nachylenie plateau wyrażające względny przyrost liczby zliczeń w prostoliniowym obszarze charakterystyki przypadający na 100V:

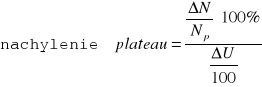
nachylenie plateau = 18.43260188 18.4

5. Przykładowe obliczenia

obliczenia dla 4. serii pomiarów:

U= 383V

n1= 174 imp./100s

n2= 169 imp./100s

nśr= 171.5 imp./100s

N=nśr*60/100= 103 imp./min.

= 10.2 imp./min.= 9.9%

Ponieważ obliczeń było mało, wypełnię ten punkt sprawozdania ładniejszym wykresem charakterystyki licznika Geigera-Millera.

6. Dyskusja błędów & wnioski

Najsampierw zaznaczę, iż doświadczenie wykonywane było znamiennego 13. dnia stycznia w piątek, co mogło być dodatkowym powodem błędów. O dacie tej nie zapomnieli również Geiger i Miller, gdyż licznik nazwany ich imionami zachowywał się dość dziwnie. Pojedyncze pomiary odstające od innych najlepiej widać na wykresie. Troszkę pomnogła tu średnia wyciągana z dwóch pomiarów, choć najlepszym sposobem uniknięcia tych błędów byłoby zapewne kilkakrotne powtórzenie wątpliwych pomiarów - niestety wymaga to dużego nakładu czasowego - ale nawet w naszym przypadku, odchylenia pomiarów od spodziewanego przebiegu są całkiem zadawalające, tzn. przyzwoicie niepozorne.

Niezły jest również przebieg charakterystyki licznika w obszarze plateau - choć nie jest on płaski, to jednak do rangi takowego pretenduje. Oczywiście kwestia odczytu zakresu plateau oraz wartości pośredniej Np jest kwestią subiektywną, jednak wartości, jakie przyjąłem, są chyba najodpowiedniejsze.

Wszelkie odchylenia mają również swe podłoże w charakterze nauki o promieniotwórczości - która oparta jest przecież na wynikach statystycznych - tak więc dopiero przy większej ilości pomiarów otrzymalibyśmy dokładnie to, czego się spodziewaliśmy.

Zakres plateau charakterystyki badanego licznika zawiera się w granicach
390-500V, zaś nachylenie plateau wynosi 18.4.

2 Piotr Ciskowski. Opracowanie doświadczenia 52.

---