2 Rezonans w obwodach elektrycznych
Po omówieniu pracy dwójników idealnych należy zająć się praca dwójników zawierających elementy L i C w stanach charakterystycznych. Stanami takimi są rezonanse elektryczne.
2.1 Pojęcia podstawowe
Rezonans jest to taki stan pracy obwodu elektrycznego, w którym reaktancja wypadkowa obwodu lub jego susceptancja wypadkowa jest równa zeru.
Obwodami rezonansowymi są nazywane obwody elektryczne, w którym występuje zjawisko rezonansu.
W stanie rezonansu napięcie i prąd na zaciskach rozpatrywanego obwodu są zgodne w fazie, tzn. argument impedancji zespolonej obwodu lub admitancji zespolonej jest równy zeru (ϕ=0).
Obwód będący w stanie rezonansu nie pobiera ze źródła mocy biernej, a mówiąc ściśle następuje zjawisko kompensacji mocy. Moc bierna indukcyjna pobierana przez obwód jest równa mocy biernej pojemnościowej. Ponieważ, jak wiadomo, znaki mocy biernej, indukcyjnej i pojemnościowej są przeciwne, dlatego w warunkach rezonansu całkowita moc bierna obwodu też jest równa zeru.
Częstotliwość, przy której reaktancja wypadkowa lub susceptancja wypadkowa obwodu jest równa zeru, jest nazywana częstotliwością rezonansową i oznaczana fr. Obwód elektryczny osiąga stan rezonansu, jeśli częstotliwość doprowadzonego do obwodu napięcia sinusoidalnego jest równa częstotliwości rezonansowej.
W zależności od sposobu połączenia elementów R,L,C, w obwodzie może wystąpić zjawisko rezonansu napięć lub zjawisko rezonansu prądów.
2.2 Rezonans napięć
Rezonans występujący w obwodzie o szeregowym połączeniu elementów R, L, C, charakteryzujący się równością reaktancji indukcyjnej i reaktancji pojemnościowej nazywamy rezonansem napięć lub rezonansem szeregowym.
Załóżmy, że do dwójnika szeregowego RLC doprowadzono napięcie sinusoidalne o wartości skutecznej zespolonej równej U i o pulsacji ω= 2πf. Dla rozpatrywanego obwodu słuszne są zależności:
UR=RI
UL=jXLI
UC=-jXCI
napięcie na zaciskach dwójnika można przedstawić zależnością:
U=UR+UL+UC =[R+j(XL-XC)]I =Z I
Rys 2.1
schemat obwodu
wykres wektorowy dla obwodu w stanie rezonansu
Zgodnie z podaną definicją, rezonans napięć wystąpi wówczas, gdy X=0, tzn.
![]()
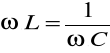
czyli:
Częstotliwość, przy której jest spełniony ten warunek, nazywa się częstotliwością rezonansowa szeregowego obwodu rezonansowego
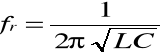
W stanie rezonansu szeregowego słuszne są więc następujące zależności:
Z = R
U = UR
UL + UC =0
UL = UC
W wyniku powyższych rozważań stwierdzamy, że w stanie rezonansu napięć:
reaktancja pojemnościowa równa się reaktancji indukcyjnej
impedancja obwodu jest równa rezystancji, a zatem argument impedancji zespolonej jest równy zeru, a oznacza iż wartość współczynnika mocy cos ϕ =1
napięcie na indukcyjności jest równe co do modułu napięciu na pojemności, a suma geometryczna tych napięć jest równa zeru
wobec X=0, prąd w obwodzie może osiągnąć bardzo dużą wartość, gdyż przy małej rezystancji R, źródło pracuje w warunkach zbliżonych do stanu zwarcia
Wprowadzimy kilka pojęć charakteryzujących obwód rezonansowy.
Impedancją falową ρ nazywamy reaktancję indukcyjną lub pojemnościową obwodu przy częstotliwości rezonansowej, czyli
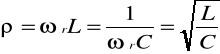
Dla obwodu szeregowego RLC będącego w warunkach rezonansu napięć, dobroć
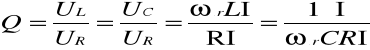
![]()
czyli
Jeżeli uwzględnimy impedancję falową ρ (107) , to otrzymamy ostatecznie
![]()
W stanie rezonansu napięcie na rezystancji jest równe napięciu doprowadzonemu do obwodu, tzn. UR=U. Z tego wynika , że dobroć obwodu Q określa, ile razy napięcie na indukcyjności lub napięcie na pojemności jest większe od napięcia na zaciskach obwodu.
Jeśli rezystancja obwodu rezonansowego jest mała, to dobroć obwodu jest duża i napięcie na elementach reaktancyjnych znacznie przekracza wartość napięcia doprowadzonego. Należy więc liczyć się ze zjawiskiem przepięcia. Obwód szeregowy RLC może znajdować się w warunkach bliskich rezonansu. Wówczas częstotliwość źródła f (lub pulsacja ω) jest różna od częstotliwości rezonansowej fr . Mówimy, że obwód jest odstrojony od rezonansu lub posługujemy się pojęciem rozstrojenia.
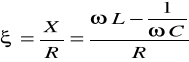
Rozstrojeniem bezwzględnym ζ nazywamy stosunek reaktancji obwodu do jego rezystancji, czyli
![]()
Z tego wynika że:
W miarę zbliżania się wartości pulsacji ω do ωr rozstrojenie bezwzględne maleje tez kąt ϕ.
Rozstrojeniem względnym δ nazywamy stosunek reaktancji obwodu do jego impedancji falowej, czyli
![]()
Wyrazimy rozstrojenie względne w nie co innej postaci. Korzystając ze wzoru na ρ, możemy wyrazić indukcyjność L i pojemność C w zależności od częstotliwości rezonansowej i impedancji falowej, czyli
![]()
![]()
Reaktancja obwodu szeregowego RLC
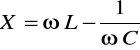
a po podstawieniu wzorów na L i na C
![]()
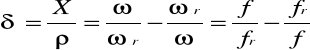
Po uwzględnieniu wzoru definicyjnego na δ, otrzymamy
![]()
Stosunek częstotliwości źródła do częstotliwości rezonansowej oznaczymy przez
wobec tego ostatecznie
![]()
W miarę zbliżania się wartości częstotliwości f do fr rozstrojenie względne maleje do zera.
Korzystając z przytoczonych wzorów, można uzyskać następujący związek między rozstrojeniem bezwzględnym a rozstrojeniem względnym.
![]()
Dobrą ilustracja zjawisk zachodzących w warunkach rezonansu i w jego pobliżu są tzw. krzywe rezonansowe, przedstawiające przebieg wielkości występujących w obwodzie rezonansowym w funkcji częstotliwości.
Na rysunku poniżej pokazano charakterystyki XL, XC, Z,ϕ,I w funkcji częstotliwości f.
Z rysunku wynika, że w miarę zbliżania się do częstotliwości rezonansowej f r impedancja obwodu maleje do wartości R, prąd zwiększa się do wartości maksymalnej , kat fazowy ϕ zbliża się do zera.
Rys. 2.2 Charakterystyki częstotliwościowe XL, XC, Z, ϕ, I
2.3 REZONANS PRĄDÓW
Rezonans występujący w obwodzie o równoległym połączeniu elementów R,L,C charakteryzujący się równością susceptancji indukcyjnej i susceptancji pojemnościowej, nazywamy rezonansem prądów lub rezonansem równoległym.
W obwodzie rezonansu prądów, przedstawionym na Rys.2.4 a) , rezystancja R odwzorowuje straty zarówno w kondensatorze, jak i w cewce. Przyjmujemy więc dla cewki i dla kondensatora schematy zastępcze równoległe.
Załóżmy, że do dwójnika równoległego RLC doprowadzono napięcie sinusoidalne o wartości skutecznej zespolonej U i o pulsacji ω=2πf . Dla rozpatrywanego obwodu są słuszne następujące zależności:
IR= GU
IL=-jBLU
IC=jBCU
a prąd dopływający do dwójnika
I=IR + IL+IC =[G + j(BC- BL)] U = Y U
Zgodnie z podana definicją, rezonans prądów wystąpi wówczas, gdy B=0, tzn.
![]()
![]()
lub
Częstotliwość przy której jest spełniony ten warunek , jest zwana częstotliwością rezonansową równoległego obwodu rezonansowego;
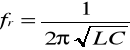
W stanie rezonansu równoległego zachodzącego w obwodzie z rys. a) są słuszne następujące zależności:
Y=G
I=IR
IL+IC=0
IL=IC
W wyniku powyższych rozważań stwierdzamy, że w stanie rezonansów prądów:
susceptancja pojemnościowa jest równa susceptancji indukcyjnej
admitancja obwodu jest równa konduktancji, a zatem argument admitancji zespolonej jest równy zeru , czyli cos
prąd w gałęzi indukcyjnej jest równy co do modułu prądowi w gałęzi pojemnościowej, a suma geometryczna tych prądów jest równa zeru
wobec B=0, prąd całkowity ma bardzo małą wartość, a przy bardzo małej konduktancji jest prawie równy zeru i źródło pracuje w warunkach zbliżonych do stanu jałowego.
Impedancję falowa ρ dla obwodu rezonansu prądów definiuje się tak samo jak dla obwodu rezonansu napięć.
Wprowadzimy teraz pojęcie dobroci obwodu rezonansowego
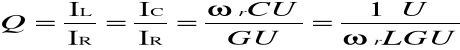
![]()
czyli
Jeżeli uwzględnimy zależność na ρ oraz G=1/R, to otrzymamy ostatecznie
![]()
Jak już wykazaliśmy, w stanie rezonansu prądów, prąd dopływający do dwójnika jest równy prądowi płynącemu w gałęzi z rezystancją tzn. I=IR.
Wobec tego z zależności określającej dobroć obwodu rezonansowego wynika, że dobroć obwodu Q określa , ile razy prąd w gałęzi z indukcyjnością lub w gałęzi z pojemnością jest większy od prądu dopływającego do obwodu rezonansowego.
Jeżeli rezystancja obwodu R jest duża (konduktancja G mała), to dobroć obwodu jest duża i prądy w gałęziach reaktancyjnych znacznie przekraczają wartość prądu dopływającego do obwodu . Należy więc się liczyć ze zjawiskiem przetężenia.
Podobnie jak dla obwodu rezonansu napięć, można wprowadzić pojęcia rozstrojenia bezwzględnego i rozstrojenia względnego charakteryzującego obwód w warunkach bliskich rezonansu.
![]()
Rozstrojenie bezwzględne
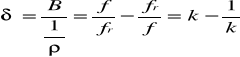
Rozstrojenie względne
Rys. 2.3 Charakterystyki częstotliwościowe BL, BC Y
Rys. 2.4 Rezonans prądów w dwójniku czteroelementowym :
schemat obwodu
wykres wektorowy dla obwodu w stanie rezonansu
Zbadamy jeszcze zjawisko rezonansu prądów w obwodzie przedstawionym na Rys.2.4 b) Obwód taki otrzymamy wówczas, gdy zarówno dla kondensatora, jak i dla cewki posłużymy się ich schematami zastępczymi szeregowymi. Analiza tego obwodu jest nieco bardziej złożona.
Oznaczmy impedancje zespolone poszczególnych gałęzi przez:
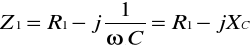
![]()
Admitancje zespolone tych gałęzi :
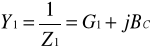
![]()
przy czym:
![]()
![]()
![]()
![]()
Prądy w poszczególnych gałęziach:
I1=Y1U = G1U + jBCU
I2=Y2U = G2U - jBLU
a prąd dopływający do obwodu
I = I1 + I2 = (G1 + G2)U + j(BC - BL)U = Y U
Zgodnie z podaną definicją , rezonans prądów wystąpi wtedy, gdy B=0 tzn.
![]()

czyli
Wyznaczymy częstotliwość rezonansową obwodu. W tym celu do wzoru tego podstawimy
![]()
![]()
![]()
![]()
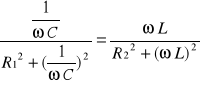
Zatem
![]()
Stąd po przekształceniach
Równanie te ma trzy rozwiązania, które kolejno rozpatrzymy:
![]()
![]()
1) Jeśli
to równanie 156 może być spełnione tylko wówczas , gdy również
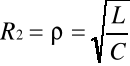
![]()
W tym przypadku rezonans wystąpi przy każdej częstotliwości. Można udowodnić że wówczas impedancja obwodu Z=ρ tzn. niezależnie od częstotliwości napięcia źródła, impedancja jest liczbą rzeczywistą; kąt fazowy obwodu φ=0 a więc obwód spełnia warunek podstawowy rezonansu.
2. Jeśli R1 ≠ ρ oraz R2 ≠ ρ to w wyniku rozwiązania równania otrzymamy częstotliwość rezonansową
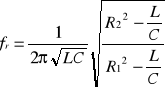
Ze wzoru tego wynika, że częstotliwość rezonansowa jest liczbą rzeczywistą, jeśli
R1 > ρ, R2 > ρ
lub
R1 < ρ, R2 < ρ
Wykres wektorowy dla stanu rezonansu przedstawiony na rysunku 2.4 b)
![]()
3. W trzecim przypadku szczególnym rezystancje R1 i R2 mogą być równe sobie, lecz nie równe impedancji falowej
Ze wzoru określającego fr z punktu 2) wynika, że przy R1 = R2 = ρ , częstotliwość rezonansowa obwodu czteroelementowego
![]()
Ma ona taką samą wartość jak częstotliwość rezonansowa obwodu przedstawionego na
Rys2.4 a) z działu „Rezonans prądów ” z wzoru (163)
Rezonans może wystąpić również w układach o połączeniu mieszanym elementów RLC. Poniżej przedstawiono kilka wybranych obwodów rezonansowych, podano wzory określające częstotliwość rezonansową i impedancje obwodu dla częstotliwości rezonansowej.
Jest oczywiste, że impedancja obwodu dostrojonego do rezonansu jest liczbą rzeczywistą; natomiast argument impedancji zespolonej musi być równe zeru.
Zjawiska rezonansu ma duże znaczenie praktyczne zarówno w technice wielkich częstotliwości, jak i w układach elektroenergetycznych. Z układami rezonansowymi spotykamy się zarówno w urządzeniach nadawczych stacji radiowo telewizyjnych, jak i w urządzeniach odbiorczych. W urządzeniach teletransmisyjnych dzięki stosowaniu układów rezonansowych, jest możliwe przekazywanie wielu informacji za pomocą jednej linii przesyłowej. Układy rezonansowe są stosowane również w wielu urządzeniach pomiarowych i w filtrach częstotliwościowych. W urządzeniach elektroenergetycznych kompensacja mocy biernej polega w istocie na tworzeniu układu rezonansowego.
W wielu urządzeniach układy rezonansowe mogą powstać w sposób przypadkowy, a z tym są związane zarówno dodatnie, jak i ujemne skutki zjawiska rezonansu. W układach rezonansu szeregowego mogą powstać znaczne przepięcia, zwane przepięciami rezonansowymi, natomiast w układach rezonansu równoległego w gałęziach obwodu mogą płynąć znaczne prądy, zwane przetężeniami rezonansowymi .
1
- 10/13 -
a)
U
UR UL UC
b)
UR=U=RI
UL=jXLI
UC=-jXCI
I
Im
Re
![]()
![]()
![]()
![]()
![]()
![]()
![]()
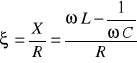
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
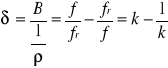
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
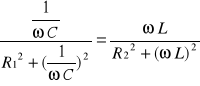
![]()
![]()
czyli
![]()
![]()
![]()
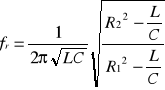
![]()
![]()
czyli
a)
b)
U
R1
C
I1
I2
R2
L
I
Im
I2
I1
I
U
Re
φ <0
φ >0
0
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129![]()
130![]()
131![]()
132![]()
133![]()
134![]()
135![]()
136![]()
137![]()
138![]()
139![]()
140![]()
141
142![]()
143![]()
144![]()
145![]()
146![]()
147![]()
148![]()
149![]()
150![]()
151![]()
152![]()
153![]()
154![]()
155![]()
156
157![]()
158![]()
159![]()
160![]()
161![]()
162![]()
163![]()
Wyszukiwarka
Podobne podstrony:
24 Badanie rezonansu w obwodach elektrycznych
Rezonans w obwodach elektrycznych v5(1), POLITECHNIKA LUBELSKA w LUBLINIE
Rezonans w obwodach elektrycznych v5(1), POLITECHNIKA LUBELSKA w LUBLINIE
Rezonans w obwodach elektrycznych v12, Elektrotechnika
Rezonans w obwodach elektrycznych v9, POLITECHNIKA LUBELSKA
Rezonans w obwodach elektrycznych v11, Elektrotechnika
Rezonans w obwodach elektrycznych v4, Elektrotechnika
Rezonans w obwodach elektrycznych, podręczniki do szkół techniczno - zawodowych i kursantów
11 Rezonans w obwodach elektrycznych
Rezonans w obwodach elektrycznych v13, Elektrotechnika
Rezonans w obwodach elektrycznych v6, Elektrotechnika
02-rezonans w obwodach elektrycznych, Ćwiczenia z elektrotechniki
Rezonans w obwodach elektrycznych v2(1), Elektrotechnika
Rezonans w obwodach elektrycznych
Rezonans w obwodach elektrycznych v3(1), Elektrotechnika
REZONANS W OBWODACH ELEKTRY4, POLITECHNIKA LUBELSKA w LUBLINIE_
Rezonans w obwodach elektrycznych, Elektrotechnika
Rezonans w obwodach elektrycznych
Ćw 11 Rezonans w obwodach elektrycznych
więcej podobnych podstron