1. Teoria przewodnictwa w metalach. Przewodnictwo - to przenoszenie ładunku elektrycznego przez ciało pod działaniem zewnętrznego pola elektrycznego. Elektrony w sieci krystalicznej odrywają się one od swoich atomów i zaczynają swobodnie poruszać się w całej objętości metalu, tworząc tzw. gaz elektronowy.
Przewodnictwo w metalach jest ściśle związane teorią kwantowa metali. W myśl tej teorii w krysztale metalicznym zewnętrzne elektrony atomów nie są związane z poszczególnymi atomami na skutek falowej natury elektronów. Z kwantowej teorii bezpośrednio wynika także, iż te elektrony przewodnictwa mogą przebyć wiele średnic atomowych nim zderza się z innym atomem. Jako L oznaczymy średnią drogę swobodną, jaka przebywa elektron miedzy kolejnymi zderzeniami. Średnim czasem miedzy zderzeniami będzie Δt=L/u gdzie u jest średnią prędkością elektronów przewodnictwa. Gdy do kawałka metalu zostanie przyłożone napięcie to każdy elektron przewodnictwa będzie działał siłą eE, a po czasie Δt każdy z tych elektronów osiągnie prędkość unoszenia vd=Δu wyprowadzona z II prawa Newtona

gdy zastąpimy Δt średnim czasem L/u otrzymujemy wzór:

Prędkość unoszenia dla wszystkich elektronów ma ten sam kierunek(-E) i powstaje wypadkowy prąd. Po każdym zderzeniu elektron traci swa prędkość.

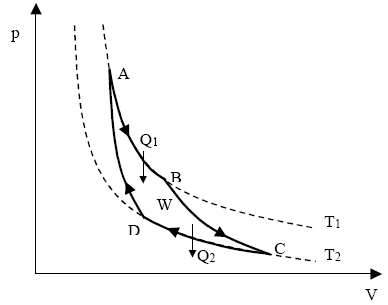
5. Opis cyklu Cartona. Sprawność silnika na bazie cyklu Cartona. Bardzo ważnym cyklem odwracalnym jest cykl Cartona. Cykl ten wyznacza granice naszych możliwości zamiany ciepła na prace. 1) Gaz znajduje się w stanie p1,V1,T1 (punkt A). Cylinder stawiamy na zbiorniku ciepla i pozwalamy, aby gaz rozprężył się izotermicznie do stanu p2,V2,T1 (punkt B). Gaz pobiera ciepło Q1. 2) Cylinder stawiamy na izolującej podstawce i pozwalamy na dalsze rozprężanie adiabatyczne gazu (np. zmniejszając obciążenie tłoka) do stanu p3,V3,T2 (punkt C) Gaz wykonuje prace przy podnoszeniu tłoka i jego temperatura spada do T2.3) Cylinder stawiamy na (zimniejszym) zbiorniku T2 i sprężamy gaz izotermicznie do stanu p4,V4,T2 (punkt D). Z gazu do zbiornika przechodzi ciepło Q2. 4) Cylinder stawiamy na izolującej podstawce i sprężamy adiabatycznie do stanu p1,V1,T1 (punkt A). Siły zewnętrzne wykonują prace i temperatura gazu podnosi się do T1. Wypadkowa praca W wykonana przez układ w czasie pełnego cyklu jest opisana przez powierzchnie zawarte wewnątrz krzywej 1,2,3,4. Wypadkowa ilość ciepła pobrana przez układ w czasie jednego cyklu wynosi Q1-Q2. Wypadkowa zmiana energii wewnętrznej wynosi zero, bo stan końcowy pokrywa się z początkowym. Z pierwszej zasady termodynamiki mamy wiec: W=Q1-Q2.

Sprawność silnika wynosi:

13. Trzy zasady termodynamiki.

Zerowa zasada termodynamiki

Zerowa zasada termodynamiki pozwala na wprowadzenie wielkości nazywanej temperaturą. 

Określenie wstępne: mówimy, że dwa ciała (układy) nieodizolowane od siebie pozostają w równowadze termicznej, jeśli nie następuje między nimi przepływ energii wewnętrznej.  

Jeżeli dwa ciała A i B są  w równowadze termicznej z ciałem C, to ciała A i B są w równowadze termicznej ze sobą. Mówimy o nich, że mają tą samą temperaturę.

Pierwsza zasada termodynamiki

Doświadczalną podstawą pierwszej zasady jest doświadczenie Joule'a i pokrewne mu, które dowodzą równoważności ciepła i pracy mechanicznej przez pokazanie możliwości całkowitej zamiany pracy na ciepło. Uznanie ciepła jako innego niż praca sposobu zmiany energii prowadzi w naturalny sposób do włączenie ciepła do zasady zachowania energii. Pierwsza zasada termodynamiki jest dokładnie tym prawem [Huang]:

Zmiana energii wewnętrznej układu równa jest dostarczonemu do układu ciepłu i pracy wykonanej nad układem przez siły zewnętrzne:

dU = dQ + dW

dU to przyrost energii wewnętrznej układu.

dQ oznacza tu ciepło dostarczone do układu z zewnątrz. Jeśli jednak układ oddaje ciepło, wówczas jego energia wewnętrzna maleje; ciepło bierzemy ze znakiem ujemnym.

dW to praca wykonana nad układem przez siły zewnętrzne. Gdy zaś układ wykonuje pracę (jak to ma miejsce podczas rozprężania się gazu), jego energia maleje - pracę bierzemy ze znakiem ujemnym. Istnieją konwencje znaków różne od tutaj przyjętej.

Druga zasada termodynamiki

Z doświadczenia wiemy, że są procesy zgodne z zasadą zachowania energii, które nigdy nie występują w przyrodzie. Zadaniem drugiej zasady termodynamiki jest włączyć do termodynamiki takie fakty doświadczalne, jej podstawą jest zdrowy rozsądek [Huang].

Wszystkie poniższe sformułowania drugiej zasady termodynamiki są równoważne:

*Clausius: Nie istnieje proces termodynamiczny, którego jedynym wynikiem byłoby pobranie ciepła ze zbiornika chłodniejszego i przekazanie go do zbiornika cieplejszego (nie jest możliwe zbudowanie idealnej maszyny chłodzącej)

*Kelvin: Nie istnieje proces termodynamiczny, którego jedynym wynikiem byłoby pobranie ciepła ze zbiornika i całkowita zamiana tego ciepła na pracę mechaniczną.

*Planck: Nie możliwe jest zbudowanie silnika termodynamicznego pracującego cyklicznie, który całe pobrane ciepło zamieniałby na pracę (nie jest możliwe zbudowanie idealnego silnika cieplnego - czyli perpetuum mobile drugiego rodzaju).

Dla sprawności silnika cieplnego, z teorią których druga zasada jest związana, oznacza to, że sprawność silników cieplnych jest mniejsza od jedności

Druga zasada termodynamiki pozwala na zdefiniowanie bezwzględnej skali temperatur Kelvina identycznej ze skalą temperatury gazu doskonałego.

Pozwala ona też na wprowadzenie użytecznej funkcji stanu nazywanej entropią. Związana jest z pojęciem procesów odwracalnych i nieodwracalnych, z kierunkiem procesów zachodzących samorzutnie w układach izolowanych, z kierunkowością zjawisk w przyrodzie. Za pomocą pojęcia entropii druga zasada termodynamiki daje się wysłowić:

Boltzmann: Entropia układu izolowanego nie maleje.

Trzecia zasada termodynamiki

Nernst,Planck: Entropia układu w temperaturze zera bezwzględnego równa jest zeru.

Wnioski:

Pojemność cieplna i ciepło właściwe dowolnej substancji w temperaturze zera bezwzględnego równe są zeru

Temperatura zera bezwzględnego nie jest osiągalna (nie jest możliwe ochłodzenie układu do temperatury zera bezwzględnego za pomocą skończonego procesu).

Trzecia zasada termodynamiki jest makroskopowym przejawem zjawisk kwantowych.

Niekiedy usłyszeć można następującą parafrazę zasad termodynamiki:

Nie możesz nic wygrać ( I ), nie możesz wyjść na swoje ( II ), nie możesz wyjść z gry ( III ) [Holiday-Resnick].

12. Równanie gazu doskonałego.

Definicja makroskopowa (termodynamiczna)

Za gaz doskonały uważać będziemy gaz spełniający łącznie prawa Boyle'a-Mariotte'a, Gay-Luusaca i Charlesa, czyli gaz dla którego w stałej temperaturze iloczyn objętość i ciśnienie są odwrotnie proporcjonalne, dla określonej objętości ma stały stosunek ciśnienia do temperatury jest stały, a pod stałym ciśnieniem - proporcjonalne są objętość i temperatura. Łącznie możemy to zapisać jedną zależnością:

Powyższy związek, definiujący gaz doskonały w ujęciu makroskopowym dotyczy oczywiście ustalonej ilości materii (ustalona masa, ustalona liczba cząsteczek, ustalona liczba moli gazu)

Definicja ta określa związek pomiędzy parametrami termodynamicznymi gazu - a więc określa gaz doskonały poprzez jego równanie stanu.

Równanie stanu - równanie Clapeyrona

Pełna postać równania stanu gazu doskonałego jest następująca:

P V = n R T

i nazywane jest ono równaniem Clapeyrona. Przy czym: P oznacza ciśnienie gazu, V - objętość, T - temperaturę, n - liczbę moli gazu a R jest tzw. stałą gazową równą R = 8, 314 J/mol·K.

Nic nie przeszkodzi, używając związku R = NA k zapisać równania następująco:

P V = N k T

gdzie k=R/NA jest stałą Boltzmanna

Na uwagę zasługuje fakt, że wymiarem prawej (i lewej) strony jest wymiar energii.

11. Prawo Archimedesa.

Prawo Archimedesa formułuje się słownie w następujący sposób:

Siła wyporu działająca na ciało zanurzone w płynie jest równa ciężarowi płynu wypartego przez to ciało

Mówiąc inaczej, gdybyśmy dokładnie takie samo ciało "wyrzeźbili" z wody (ale nie z lodu, bo lód jest lżejszy niż woda!), to ciężar tej "rzeźby" dałby nam wartość siły wyporu w wodzie. Oczywiście nie musimy dokładnie rzeźbić ciała - wystarczy, że po prostu weźmiemy tylko tę ilość "materiału" na naszą rzeźbę - czyli wodę mającą tyle samo objętości co ciało.

Wnioski wyciągnięte z tego prawa:

*siła wyporu jest tym większa, im cięższy jest płyn - większa siła wyporu jest w wodzie, niż w powietrzu i większa w rtęci, niż w wodzie.

*siła wyporu jest tym większa, im większe (rozmiarami, objętością) jest ciało (a przynajmniej jego zanurzona część)

Wzór na siłę wyporu

Siłę wyporu da się zapisać wzorem:

F_wyporu = ρ_płynu * g * V_zanurzona

gdzie:

ρ_płynu - gęstość płynu (cieczy, gazu) w którym zanurzone jest ciało - [w układzie SI w kg/m^3]

V_zanurzona - objętość tej części ciała, która jest zanurzona w płynie [w układzie SI w m^3]

g - przyspieszenie ziemskie [w układzie SI w m/s^2]

8. Praca wykonywana przez gaz w trakcie rozprężania adiabatycznego.

Przy rozprężaniu adiabatycznym część energii wewnętrznej gazu zamienia się w pracę mechaniczną. Praca wykonana przez 1 mol gazu doskonałego przy jego rozprężaniu od V1 do V2 wynosi:

i jest równy zaznaczonemu polu pod krzywą na wykresie. Ponieważ:

, więc
, po podstawianiu tego do całki otrzymujemy:

9. Praca wykonywana przez gaz w trakcie rozprężania izotermicznego. Chcąc obliczyć pracę mechaniczną dostarczoną otoczeniu podczas ruchu tłoka przy rozprężaniu izotermicznym gazu tak, że jego objętość rośnie od V1 do V2 trzeba utrzymywać stałą temperaturę ścian cylindra, a tłok musi się poruszać wolno, żeby gaz miał czas na pozostawanie w równowadze termicznej ze ściankami. (Gdybyśmy pozwolili gazowi szybko się rozprężać, dążyłby on wraz z rozprężaniem się do ochłodzenia, ponieważ część energii wewnętrznej gazu zamieniłaby się w energię mechaniczną,
.

Przy rozprężaniu izotermicznym ciepło musi przepływać z termostatu do rozprężającego się gazu, żeby utrzymywać jego temperaturę. Ciepło pobrane przez gaz musi być równe pracy mechanicznej wykonanej przez gaz. Wynika to także z pierwszej zasady termodynamiki,
. Ponieważ dla rozprężania izotermicznego
, więc mamy

Dla gazu doskonałego za wyrażenie podcałkowe podstawiamy:

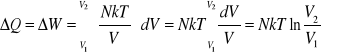
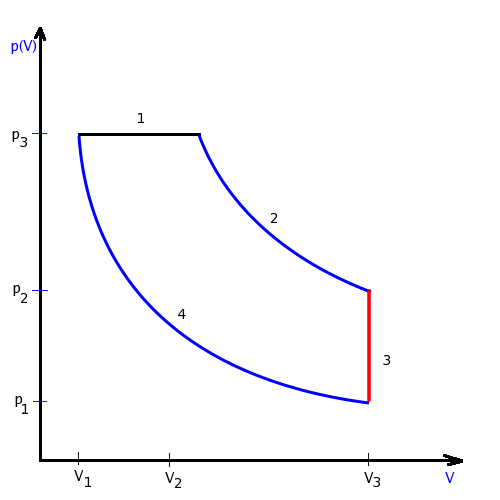
6. Cykl i sprawność silnika Otta.

odwracalny proces kołowy składający się z następujących czterech procesów składowych:

*sprężanie adiabatyczne

*ogrzewanie izochoryczne (wskutek spalania mieszanki, silnik spalinowy)

*ekspansja adiabatyczna

*chłodzenie izochoryczne

Na zasadzie cyklu Otta działają tłokowe silniki spalinowe z zapłonem iskrowym.

Sprawność:

gdzie:

R - stała gazowa

cv - ciepło właściwe

Cykl Otta jest stosowany w silnikach czterosuwowych, o zapłonie iskrowym.

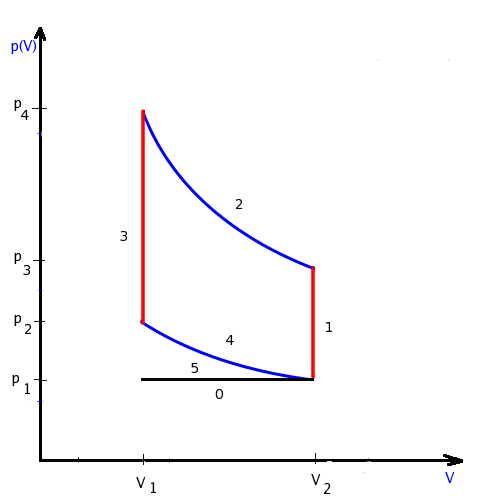
7. Cykl i sprawność silnika Diesla.

Cykl Diesla to przemiana termodynamiczna złożona z następujących po sobie przemian: izobarycznego, adiabatycznego, izochorycznego oraz adiabatycznego sprężania. Cykl Diesla jest procesem kołowym i odwracalnym. Na zasadzie tego cyklu opiera się działanie silników Diesla (w przeciwieństwie do silników o zapłonie iskrowym, które pracują w cyklu Otta).

Cykl składa się z następujących procesów:

izobaryczne rozprężanie - w silniku Diesla w tym etapie spalana jest mieszanka tak, by następowało podgrzanie przy stałym ciśnieniu (rozprężanie z objętości V1 do objętości V2)

adiabatyczne rozprężanie - z V2 do V3

izochoryczne sprężanie - stała objętość V3

adiabatyczne sprężanie - do objętości V1

Sprawność cyklu:

gdzie:

cv - ciepło właściwe przy stałej objętości

cp - ciepło właściwe przy stałym ciśnieniu

γ - stała zależna dla danego gazu w przemianie adiabatycznej pVγ = const. Dla gazu doskonałego γ=cp/cv

Nie jest to najlepsza sprawność (lepszą ma cykl Carnota) jednak jest lepsza od sprawności w cyklu Otta

4. Porównanie siły grawitacyjnej i elektrostatycznej.

Wartość siły grawitacyjnej wyraża się wzorem:

F_g - siła grawitacyjna,

G - stała grawitacji,

m_1 oraz m_2 - masy ciał,

r - odległość między środkami ciał.

Działające siły: Słabe w porównaniu z siłami pola elektrostatycznego

Wartość siły oddziaływania dwóch ładunków punktowych (elektrostatycznej - kulombowskiej) wyraża się wzorem

F_e - siła kulombowska,

k - stała(współczynnik proporcjonalnosci),

q_1 oraz q_2 - ładunki,

r - odległość między ładunkami.

Działające siły: Silne

Porównanie sił grawitacyjnych i elektrostatycznych dla dwóch elektronów wzajemnie oddziałujących na siebie z odległości 1 metra

masa elektronu:

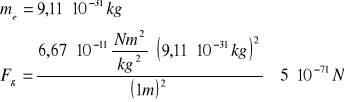
ładunek elektronu:

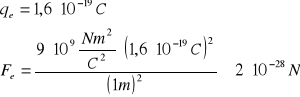
stosunek tych sił:

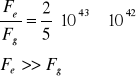
Te dwa rodzaje sił są niezależne od siebie i nie istnieje żaden ustalony związek między masą ciała i jego ładunkiem. W przeciwieństwie do masy, ładunek elektryczny może być bądź dodatni bądź ujemny. Dwa ładunki o przeciwnych znakach (ładunki różnoimienne) doznają działania siły odpychającej.

3. Prawa Gaussa dla elektrostatyki.

Strumień wektora indukcji pola elektrostatycznego D przechodzącego przez dowolną, zamkniętą powierzchnię S, jest równy całkowitemu ładunkowi zawartemu wewnątrz tej powierzchni. Φ=Qcałk

Przykład powierzchnia zamknięta Z i umieszczone w nim 2 ładunki Q1 i Q2. Całkowita liczba linii sił przecinających tę powierzchnię jest równa:

Φcałk=

korzystając ze wzoru

(gdzie ko to współczynnik proporcjonalności, która wyznacza się doświadczalnie, inaczej współczynnik Coulomba) otrzymujemy

Φcałk=(4πkoQ1)+(4πkoQ2)=4πko*(Q1+Q2)

Podobne rozumowania można przeprowadzić dla układu n ładunków wewnątrz zamkniętej powierzchni:

, gdzie Qwewn jest wypadkowym ładunkiem zawartym wewnątrz zamkniętej powierzchni. Jeżeli Q jest ujemne to linie wchodzą do ciała. Linie mogą się zaczynać lub kończyć jedynie na ładunkach, a wszędzie indziej są ciągłe. Niezależnie czy na zewnątrz zamkniętej powierzchni znajdują się ładunki, czy też nie to Prawo Gaussa jest prawdziwe. Każda linia wchodząca do obszaru zawartego wewnątrz powierzchni musi z niego wychodzić. Więc wypadkowa liczba linii wychodzących z tego obszaru jest równa zeru. ( Linia wchodząca jest linią ujemna, a linia wychodząca dodatnią). Ciała przeważnie można podzielić na dwa rodzaje: przewodzące (przewodniki) i nie przewodzące ( izolatory).

W izolatorze nadmiarowy ładunek może być rozmieszczony na powierzchni lub wewnątrz izolatora i będzie się tam utrzymywał. Natomiast przewodniki zawierają dużą liczbę swobodnych elektronów, które nie są związane z poszczególnymi atomami. Z tego względu pole elektryczne mogłoby istnieć tylko przez krótki okres czasu, ponieważ swobodne elektrony poruszały by się pod wpływem pola i zbierały się na powierzchni dopóki nie wytworzy się pole elektryczne równe co do wartości, lecz przeciwnie skierowane względem pola zewnętrznego. Na podstawie prawa Gaussa można stwierdzić, że wypadkowy ładunek wewnątrz przewodnika jest równy zero.

2. Rozkłady natężenia pola elektrycznego od wybranych rozkładów ładunku.

Liniowe rozkłady ładunków.

Najpierw rozważmy pole w odległości r od jednorodnie naładowanego pręta o długości znacznie większej od r. Niech λ będzie ładunkiem na jednostkę długości pręta, czyli liniową gęstością ładunku. Jako powierzchnię Gaussa wybieramy walec o długości L. Ta powierzchnia otacza ładunek
. Z prawa Gaussa otrzymujemy

Wykorzystując ponownie argumenty wynikające z symetrii problemu wnioskujemy, że linie pola E mogą rozchodzić się tylko radialnie. Stąd wynika, iż wektory E i dA tworzą kąty proste na obu powierzchniach zamykających walec oraz, że są równoległe na zakrzywionej powierzchni walca. Ponieważ E*dA jest równe zeru na powierzchniach zamykających walec, mamy

Porównując to wyrażenie do
otrzymujemy

(pole pochodzące od ładunku liniowego)

Następnie obliczamy pole wewnątrz jednorodnie naładowanego pręta. Ponownie wybieramy powierzchnie Gaussa w kształcie walca o długości L, lecz tym razem o promieniu r<R. Jeżeli ρ jest ładunkiem pręta na jednostkę objętości, to ładunek otoczony przez walec, jest równy
. Z prawa Gaussa wynika

(wewnątrz pręta)

Pole możemy wyrazić również za pomocą λ pisząc
. Wtedy

Płaskie rozkłady ładunków.

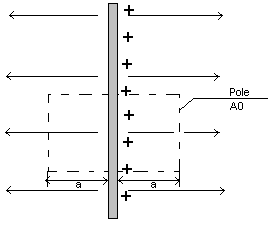
Obliczamy pole wytwarzane przez jednorodnie naładowaną nieskończoną płaszczyznę. Niech σ oznacza ładunek na jednostkę powierzchni, czyli powierzchniową gęstość ładunku. Powierzchnie całkowania wybieramy w kształcie fiolki, czyli walca z płaskimi podstawami o polu powierzchni A₀, przy czym każda podstawa walca jest odległa o a od płyty. Ładunek otoczony przez taka powierzchnie jest równy
. Ponieważ ani lewa, ani prawa strona płyty nie jest wyróżniona, linie strumienia muszą jednakowo wychodzić w obie strony. Przyczynek do całki powierzchniowej pochodzący od każdej podstawy walca jest równy EA₀. Ponieważ walec ma dwie podstawy, zatem
. Z prawa Gaussa otrzymujemy

(naładowana płyta)

10. Ciepło właściwe w przemianie izobarycznej i izochorycznej.

Molowe ciepło właściwe gazu jest to ilość ciepła do podniesienia temperatury 1 mola gazu o 1 stopień.

Ciepło właściwe w stałej objętości:

Symbol C_V

dU=dQ-PdV podstawiając tu dV=0 otrzymamy dQ=dU a stąd mamy i skoro
dla mola jednoatomowego gazu doskonałego, zatem
czyli

Średnia energia wewnętrzna na cząsteczkę wynosi:

, a dla 1 mola wynosi:

Trudnością w mechanice klasycznej jest to że przewiduje ona iż ciepło właściwe powinno być nie zależne od temperatury. Jednak dla wszystkich gazów oprócz gazów jednoatomowych C_V rośnie wraz ze wzrostem temperatury.

Ciepło właściwe przy stałym ciśnieniu:

Symbol C_P

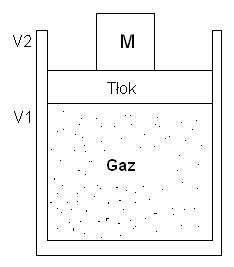
Jeśli mol gazu utrzymujemy pod stałym ciśnieniem i pozwalamy ciepłu dopływać do gazu, to wzrośnie jego objętość i pewna ilość ciepła PΔV zamieni się w pracę mechaniczną. Zgodnie z

dQ=dU+PdV. (1)

Skoro U zależy od T więc:

dU=CVdT (2)

dQ=CVdT+PdV (3)

Dla gazu doskonałego:

i

Po podstawieniu tego równania (3) mamy:

co z definicji jest równe C_p czyli ciepłu właściwemu przy stałym ciśnieniu. Tak więc dla gazu doskonałego mamy: C_P-C_V=R

DOPISANE:

2. Rozkłady natężenia pola elektrycznego od wybranych rozkładów ładunku.

Jednorodnie naładowana sfera

Rozpatrzmy jednorodnie naładowana powierzchnie kulista.

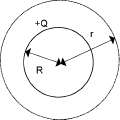
W dowolnym punkcie sfery E \ \ S (prostopadłe do powierzchni) wiec

Zgodnie z prawem Gaussa:

E(4πr²) = Q/Eo

Czyli:

dla r> R (tak jakby cały ładunek skupiony był w środku sfery). Dla r<R, E=0.

Jednorodnie naładowana kula

Przewodniki - równoważne sferze, bo ładunek na powierzchni. Izolator - równoważny szeregowi współśrodkowych sfer.

gdzie Q_wewn. = Q{rⁱIR³') (stosunek objętości kuli o promieniu r do objętości kuli o pro­mieniu i?, rysunek).

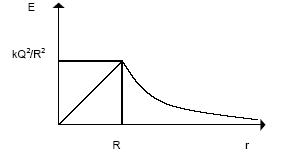
Wykres E w funkcji odległości od środka jednorodnie naładowanej kuli jest pokazany obok.

Liniowe rozkłady ładunków

Liczymy pole E w odległości r od jednorodnie naładowanego pręta (drutu) o długo­ści r.

Wprowadzamy liniowa gestosc ładunku A (ładunek na jednostkę długości). Jako powierzchnie Gaussa wybieramy walec (możemy wybierać dowolnie). Z prawa Gaussa

E jest równoległe do wektora S i ma taka sama wartość w każdym punkcie powierzchni wiec

Teraz pole wewnątrz. Wybieramy powierzchnie Gaussa o promieniu r <R.

Ładunek wewnątrz powierzchni Gaussa Q_wew„. = ro*pi*r*L, gdzie ro - gestosc objętościowa ładunku. Z prawa Gaussa otrzymujemy

Płaskie rozkłady ładunków

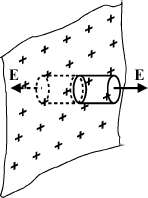
Obliczamy pole od nieskończonej jednorodnie naładowanej płaszczyzny.

Ładunek otoczony przez powierzchnie Gaussa jest równy Q_wewn = oS, gdzie o jest ge-stoscia powierzchniowa, a S powierzchnia podstawy walca. Z prawa Gaussa

gdzie czynnik 2 odpowiada dwom podstawom walca. Ostatecznie otrzymujemy

Wiele zastosowań dotyczy układu dwóch, płaskich równoległych płyt (kondensator płaski).

*Pole wytwarzane przez płytę "po lewej stronie" (rysunek poniżej) jest równe E_minus=σ/2ε₀ i skierowane ku płycie.

Pole wytwarzane przez płytę po prawej E_plus=σ/ε₀ i skierowane jest od płyty.

11. Prawo Archimedesa.

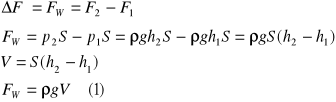
gdzie:

- wartość siły wyporu

 - gęstość cieczy
g - ziemskie przyspieszenie grawitacyjne

V- objętość ciała Ze wzoru


otrzymujemy

(2).
Jest to masa wypartej cieczy, bo przy całkowitym zanurzeniu objętość ciała równa się objętości wypartej cieczy.Po podstawieniu (2) do (1)


czyli
gdzie, Q = ciężar wypartej cieczy

Prawo Archimedesa:Na ciało zanurzone w cieczy działa siła wyporu zwrócona pionowo do góry, równa co do wartości ciężarowi wypartej cieczy.

Z powyższych rozważań wynika, że ciało tonie, gdy
, czyli gęstość ciała jest większa od gęstości cieczy, w której ciało to jest zanurzone. Ciała o gęstości równej lub mniejszej od gęstości cieczy pływają. W takich przypadkach równowaga zapewniona jest przez równość
. Gdy gęstości są równe, ciało „unosi się” między powierzchnią i dnem, a dla
wypływa. Po wypłynięciu na powierzchnię, ciało zanurza się tylko częścią swojej objętości. Oznaczając ją przez V₁ otrzymujemy:

Oznacza to, że stosunek objętości części zanurzonej do całej objętości ciała jest równy stosunkowi gęstości ciała do gęstości cieczy. Doskonałym przykładem ilustrującym to zjawisko są góry lodowe, które ponad powierzchnię wystają tylko w niewielkim stopniu, ponieważ lód ma nieco mniejszą gęstość niż woda.

13. Zasady termodynamiki:

a) zerowa zasada termodynamiki - izolowane ciała będące w kontakcie ze sobą osiągają równowagę termiczną:

E_k1=E_k2

b) I zasada termodynamiki - ciepło pobrane przez układ powoduje wzrost energii wewnętrznej układu oraz pracę wykonaną przez ten układ.

∆Q = ∆U_wew + ∆W

∆U_wew = ∆Q - ∆W

Jeżeli rozważany układ to cylinder z gazem działającym na tłok siła F, to:

∆W = F*∆l = P*s*∆l = P*∆V

c) II zasada termodynamiki - mówi, że w układzie zamkniętym w procesach odwracalnych, ciepło (nie będące funkcją stanu) ma czynnik całkujący w postaci odwrotności temperatury, co prowadzi do pojęcia entropii jako funkcji stanu . Zatem poprawne sformułowanie II zasady termodynamiki jest następujące:

„ W dowolnym procesie (odwracalnym lub nieodwracalnym) w układzie zamkniętym zmiana entropii ∆S >= ∆Q/T”, lub jeszcze prościej:

„W układzie zamkniętym w dowolnym procesie entropia nigdy nie maleje”

d) III zasada termodynamiki - głosi, że entropia substancji tworzących doskonałe kryształy dąży do 0 gdy temperatura dąży do 0 K.

Mówiąc jaśniej, gdyby udało się schłodzić jakąś substancję do 0 K i gdyby ona utworzyła kryształ doskonały to jej entropia musiałaby przyjąć wartość 0. Jest to jednak technicznie, a także formalnie niewykonalne, dlatego definicja trzeciej zasady termodynamiki w formie: „entropia kryształu doskonałego w temperaturze zera bezwzględnego jest równa 0” nie jest poprawna, choć intuicyjnie akceptowalna.

Pytania:

1. Teoria przewodnictwa w metalach.

2. Rozkłady natężenia pola elektrycznego od wybranych rozkładów ładunku.

3. Prawa Gaussa dla elektrostatyki.

4. Porównanie siły grawitacyjnej i elektrostatycznej.

5. Cykl i sprawność silnika Carnota.

6. Cykl i sprawność silnika Otta.

7. Cykl i sprawność silnika Diesla.

8. Praca wykonywana przez gaz w trakcie rozprężania adiabatycznego.

9. Praca wykonywana przez gaz w trakcie rozprężania izotermicznego.

10. Ciepło właściwe w przemianie izobarycznej i izochorycznej.

11. Prawo Archimedesa.

12. Równanie gazu doskonałego.

13. Trzy zasady termodynamiki.

Kompilacja i duża część zasług przy tworzeniu: Błażeju (plik pochodzi z blazejus.rox.pl)

Podziękowania: inż., Dante, manutd, Maćka i jego kolegi ;), Rzeźnik, TeQ, Krystian, SmokOO, Darka Rackiego, pawello

jak ktoś jeszcze mi dawał, co tu jest - niech się do mnie zgłosi ;>

---