![]()
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA INSTYTUT POLITECHNICZNY |
||||
2004/2005 |
LABORATORIUM Z AUTOMATYKI I STEROWANIA |
|||
Ćwiczenie nr 1 |
BADANIE CZŁONU INERCYJNEGO I RZĘDU |
|||
Budowa i Eksploatacja Maszyn ST. Zaoczne Semestr III |
Dyksik Arnold Stefaniak Łukasz Kania Mateusz |
|||
Data wykonania |
|
Data |
Ocena |
Podpis |
2005-04-04 |
T |
|
|
|
|
S |
|
|
|
Cel ćwiczenia
Celem ćwiczenia jest zbadanie właściwości dynamicznych członu inercyjnego pierwszego rzędu opisanego następującą transmitancją:
![]()
Schemat blokowy badanych układów
Przebieg ćwiczenia
Wymuszenie typu skok jednostkowy
Odpowiedź układu jest następująca:
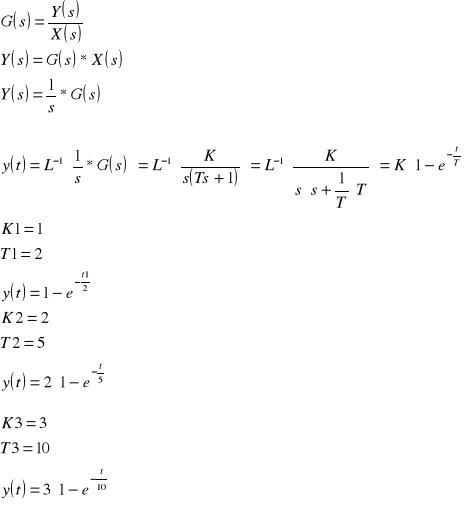
Wymuszenie typu impuls jednostkowy
Odpowiedź układu jest następującą:
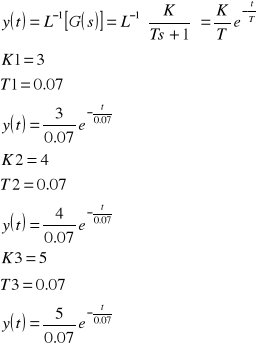
Wymuszenie typu sygnał liniowo narastający
Odpowiedź układu jest następująca:
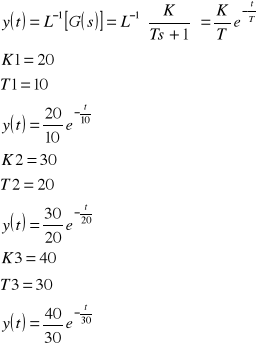
Wyznaczanie charakterystyki amplitudowo-fazowej (wykres Nyquista).
Odpowiedź układu jest następująca:
![]()
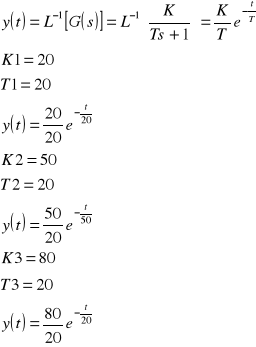
Wyznaczanie charakterystyki amplitudowo-fazowej (wykres Bodego).
Odpowiedź układu jest następująca:
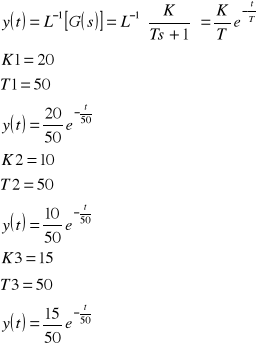
Wnioski
Skoro, więc naszemu tajemniczemu na razie obiektowi podajemy na wejście sygnał u(t), czyli zmienny w czasie, a na wyjściu oczekujemy sygnału y(t) - również zmiennego w czasie, to moglibyśmy określić nasz obiekt mianem obiekt dynamiczny. Sygnał wyjściowy jest pomnożonym sygnałem wejściowym przez stały współczynnik, ale jak rozumieć wzór opisujący obiekt inercyjny obiekt inercyjny to taki obiekt proporcjonalny, którego wyjście jest pomniejszone o szybkość zmian, jakie się na tym wyjściu dokonują pomnożoną przez tzw. stałą czasową T., Ponieważ, jak widać, przez ową stała czasową mnożona jest pochodna sygnału wyjściowego, więc odgrywa ona ważną rolę w tym, jak szybko będą dokonywały się zmiany na wyjściu. Im mniejsza jest stała czasowa, tym bardziej obiekt inercyjny przypomina obiekt proporcjonalny, bo zmiany na wyjściu mogą dokonywać się szybciej. Obiekt inercyjny ma bardzo ważna cechę:, jeśli wymuszenie nie będzie jakimś szczególnym sygnałem pochodzący z tzw. dziedziny dystrybucji, do której należy delta, Diraca, to obiekt inercyjny zapewnia ciągłość sygnału na wyjściu. Tak, więc jeśli nawet wymuszenie (wygnał wejściowy) będzie nieciągłe, to mimo to sygnał wyjściowy będzie ciągły i będzie się starał nadążać za wymuszeniem. Przypuśćmy, że sygnały u(t) i y(t) miały do chwili to=0 wartości 0 (zero), zaś w chwili to=0 u(t)skoczył na wartość 1 (jeden) i utrzymywał już zawsze tą wartość. Sygnał taki zwie się skokiem jednostkowym. Obiekt inercyjny zachowa sygnał w chwili to, natomiast gwałtownie zmieni pochodną i to tak ją zmieni, żeby oczywiście spełnione było równanie:
Ponieważ y(0)=0, u(0)=1, więc pochodna y'(0)=K/T.
Czyli widać, że obiekt inercyjny zachowuje ciągłość sygnału na wyjściu, ale nie zachowuje ciągłości pochodnej sygnału na wyjściu.
Wykres Nyquista Ocenia on stabilność układu zamkniętego na podstawie badania charakterystyki częstotliwościowej układu otwartego. Jeżeli sygnał sinusoidalnie zmienny, który może być składnikiem widma zakłóceń wniknie w dowolnym miejscu do układu, to po obiegnięciu pętli, jaką tworzą elementy zamkniętego układu ulega przetworzeniu polegającemu na zmianie amplitudy i fazy. Ze względu na niedodatni znak sprzężenia zwrotnego, taki sygnał o częstotliwości, przy której po przejściu przez elementy tworzące pętlę zmieni fazę na przeciwną, ulegnie podtrzymaniu. Jeżeli moduł transmitancji widmowej pętli będzie dla tej częstotliwości większy od jedności to po każdym obiegnięciu pętli amplituda sygnału zwiększy się. Charakterystyki Bodego są charakterystykami logarytmicznymi.
W praktyce interesuje nas jedynie część wykresu charakterystyki dla pulsacji dodatnich. Strzałka na charakterystyce określa wzrost pulsacji Z wykresu można odczytać maksimum charakterystyki amplitudowej A()=K dla pulsacji =0. Przy dążącej do nieskończoności amplituda zmierza do zera a faza do -90 Z wykresu Nyquista możemy odczytać, że =0 gdy punkt charakterystyki leży na dodatniej półosi rzeczywistej. Amplitudę odczytujemy jako odległość danego punktu charakterystyki od środka układu współrzędnych.
Logarytmiczna charakterystyka modułu - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy pulsację w skali logarytmicznej, a na osi rzędnych moduł M(w) transmitancji widmowej G(jw) wyrażony w decybelach odkładamy na skali liniowej
Logarytmiczna charakterystyka fazy - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy również pulsację w skali logarytmicznej, a na osi rzędnych faza () w skali liniowej wyrażoną w stopniach Charakterystyki te łącznie w pełni opisują liniowy układ dynamiczny. Charakterystyki Bodego mają tę zaletę, iż można je łatwo przedstawić za pomocą asymptot. Taka przybliżona charakterystyka zwana charakterystyką asymptotyczną jest linią łamaną składającą się z odcinków asymptot charakterystyki rzeczywistej. Prostota polega na tym, że w transmitancjach widmowych występuje kilka typowych wyrażeń o charakterystycznym rozłożeniu zer i biegunów i można do nich stosować kilka prostych reguł.
Aproksymację zaczynamy dla pulsacji → 0.
Dla charakterystyki amplitudowej zasady są następujące:
Dla czynnika niezależnego od częstotliwości (wzmocnienie) asymptota jest płaska i ma wartość 20log(K1), K1=20 stąd amplituda A( )| =0=20log(20) = 26,02dB
Dla charakterystyki częstotliwościowej fazowej zasady są następujące:
Czynnik niezależny (wzmocnienie) nie wpływa na charakterystykę fazową,
W punkcie występowania bieguna odejmujemy od bieżącej fazy 90 i szkicujemy krzywą przechodzącą przez środek
W punkcie występowania zera natomiast dodajemy 90
Wymuszenie
X(s)
Człon inercyjny I rzędu G(s)
Oscyloskop
Y(s)