Ćwiczenie nr 6

Temat: Wyznaczanie momentu bezwładności bryły za pomocą

wahadła torsyjnego.

1. PODSTAWY TEORETYCZNE

Momentem bezwładności nazywamy sumę iloczynów mas wszystkich punktów materialnych ciała i kwadratu odległości od osi obrotu:

Moment bezwładności tego układu nie jest równy momentowi bezwładności ciała sztywnego, lecz będzie do niego dążył, gdy liczba sześcianików dążyć będzie do nieskończoności. Zatem momentem bezwładności ciała sztywnego jest granicą momentu bezwładności I:

Wyprowadzenie wzoru na moment bezwładności walca:

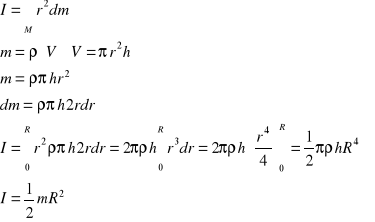
II. OPIS PRZEPROWADZONEGO DOŚWIADCZENIA

W doświadczeniu należało wyznaczyć momenty bezwładności dwóch brył. Pierwszą był walec, a drugą prostopadłościan z systemem otworków w ścianach zapewniającym różnorakie usytuowanie osi obrotu względem osi symetrii bryły.

Przyrządem umożliwiającym zbadanie momentu bezwładności obu tych brył była waga torsyjna. Zadaniem urządzenia było zliczanie czasu pełnych 20 okresów drgań badanej bryły.

Schemat urządzenia przedstawiony został poniżej.

III. WYPROWADZENIE WZORU ROBOCZEGO

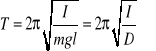
- D - moment kierujący wahadła

- okres drgań przy nieobciążonym stoliku

- okres drgań przy obciążeniu bryłą foremną o znanym momencie bezwładności

Podnosząc powyższe równania do kwadratu, a następnie odejmując stronami otrzymamy:

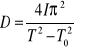
- okres drgań przy obciążeniu bryłą o nieznanym momencie bezwładności

Podnosząc równania na
do kwadratu, a następnie odejmując stronami otrzymamy:

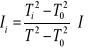
IV. OBLICZENIA I WYZNACZANIE NIEPEWNOŚCI POMIARU

1) Pomiar czasu drgań dla ramki bez obciążenia

L.p.	Czas t 20 okresów [s]
1	35,867	1,79335	0,0002	3,8E-08
2	35,874	1,7937	-0,00016	2,4E-08
3	35,871	1,79355	-5E-06	2,5E-11
4	35,869	1,79345	9,5E-05	9E-09
5	35,863	1,79315	0,00039	1,6E-07
6	35,872	1,7936	-5,5E-05	3E-09
7	35,870	1,7935	4,5E-05	2E-09
8	35,871	1,79355	-5E-06	2,5E-11
9	35,876	1,7938	-0,00025	6,5E-08
10	35,876	1,7938	-0,00025	6,5E-08

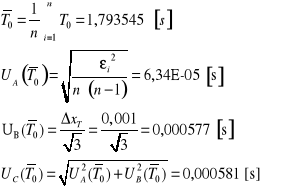
2) Pomiar czasu drgań dla ramki przy obciążeniu bryłą foremną (walec) oraz wyznaczenie momentu bezwładności

L.p.	Czas t 20 okresów [s]
1	41,746	2,0873	-0,012295	0,00015117
2	41,460	2,073	0,002005	4,02E-06
3	41,482	2,0741	0,000905	8,1902E-07
4	41,474	2,0737	0,001305	1,703E-06
5	41,476	2,0738	0,001205	1,452E-06
6	41,472	2,0736	0,001405	1,974E-06
7	41,469	2,07345	0,001555	2,418E-06
8	41,470	2,0735	0,001505	2,265E-06
9	41,472	2,0736	0,001405	1,974E-06
10	41,480	2,074	0,001005	1,01E-06

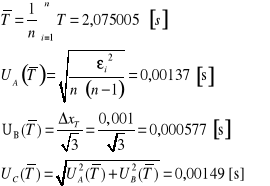
a) Wyznaczenie momentu bezwładności walca

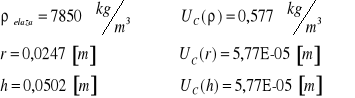
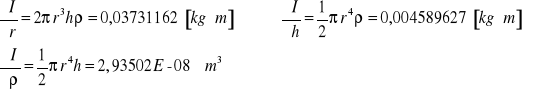
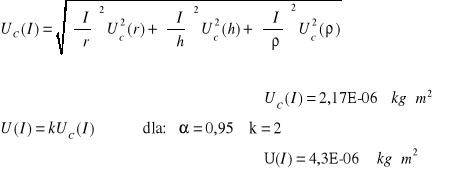
3) Pomiar czasu drgań dla ramki przy obciążeniu bryłą o nieznanym momencie bezwładności dla trzech różnych osi obrotu i obliczenie momentu bezwładności

a) Oś nr 1

L.p.	Czas t 20 okresów [s]
1	68,295	3,41475	-0,0002	4,8E-08
2	68,299	3,41495	-0,0004	1,8E-07
3	68,284	3,4142	0,00033	1,1E-07
4	68,282	3,4141	0,00043	1,8E-07
5	68,280	3,414	0,00053	2,8E-07
6	68,279	3,41395	0,00058	3,4E-07
7	68,280	3,414	0,00053	2,8E-07
8	68,302	3,4151	-0,0006	3,2E-07
9	68,303	3,41515	-0,0006	3,8E-07
10	68,302	3,4151	-0,0006	3,2E-07

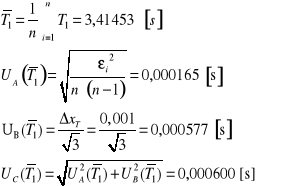
Obliczanie momentu bezwładności względem osi 1

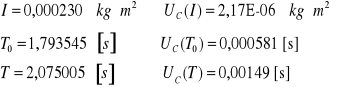
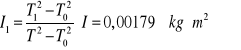
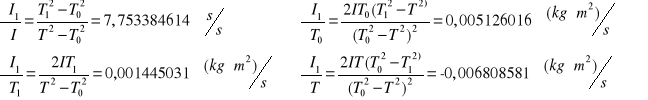
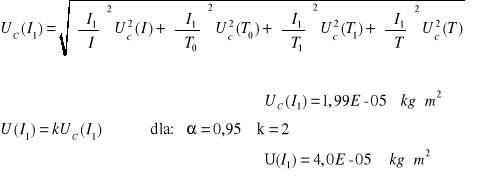
b) Oś nr 2

L.p.	Czas t 20 okresów [s]
1	72,449	3,62245	-0,00065	4,16E-07
2	72,435	3,62175	5,5E-05	3,02E-09
3	72,447	3,62235	-0,00055	2,97E-07
4	72,442	3,6221	-0,00029	8,7E-08
5	72,446	3,6223	-0,0005	2,45E-07
6	72,445	3,62225	-0,00045	1,98E-07
7	72,442	3,6221	-0,00029	8,7E-08
8	72,436	3,6218	5E-06	2,5E-11
9	72,393	3,61965	0,002155	4,64E-06
10	72,426	3,6213	0,000505	2,55E-07

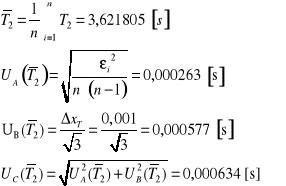
Obliczanie momentu bezwładności względem osi 2

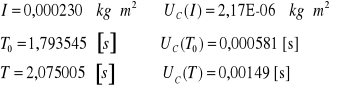
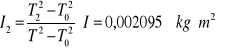
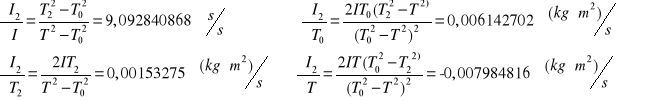
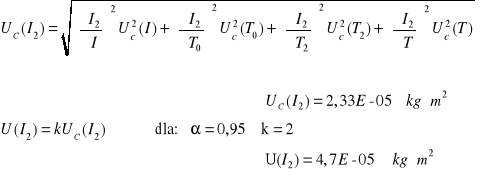
c) Oś nr 3

L.p.	Czas t 20 okresów [s]
1	53,031	2,65155	0,000115	1,32E-08
2	53,021	2,65105	0,000615	3,78E-07
3	53,028	2,6514	0,000265	7,02E-08
4	53,037	2,65185	-0,00019	3,42E-08
5	53,034	2,6517	-3,5E-05	1,23E-09
6	53,033	2,65165	1,5E-05	2,25E-10
7	53,035	2,65175	-8,5E-05	7,22E-09
8	53,033	2,65165	1,5E-05	2,25E-10
9	53,039	2,65195	-0,00029	8,12E-08
10	53,042	2,6521	-0,00043	1,89E-07

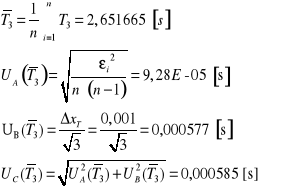
Obliczanie momentu bezwładności względem osi 3

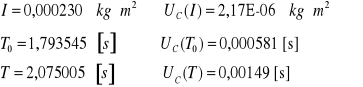
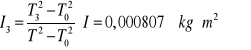
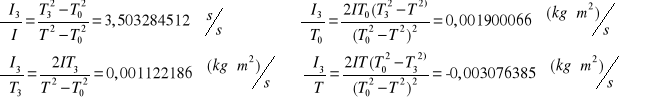
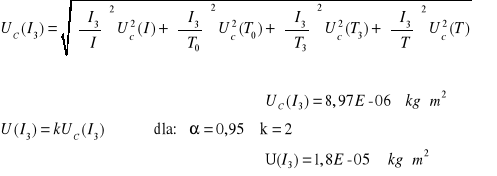
V. WNIOSKI

- Zaobserwowaliśmy, że obliczone momenty bezwładności badanej bryły względem poszczególnych osi obrotu różnią się.

---