5.4. Tensor momentu bezwładności i twierdzenie Steinera.
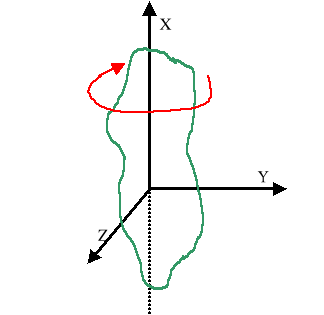
![]()
![]()
więc
![]()
z rachunku wektorowego wiadomo: ![]()
więc:
![]()
zatem ![]()
ale ![]()
Zatem ![]()
Składowe wektora ![]()
:
![]()
![]()
![]()
Porządkując:
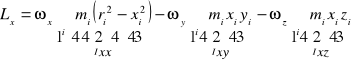
gdzie:
![]()
skoro ![]()
więc:
![]()
![]()
![]()
Tensor momentu bezwładności osi głównych:
![]()
![]()
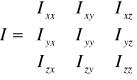
![]()
Ostatecznie 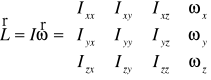
Własności tensora momentu bezwładności:
Symetryczny;
Można zdiagonalizować do postaci: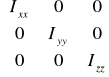
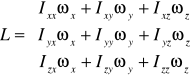
![]()
![]()
Suma jest izotropowa, czyli jest niezależna od orientacji ciała względem osi układu. Gdy ciało ma symetrię osiową względem osi OZ to ![]()
.
5.5. Przykłady obliczeń momentów bezwładności.
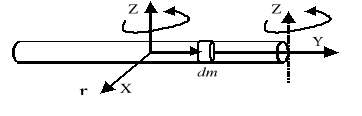
Liniowy rozkład masy.
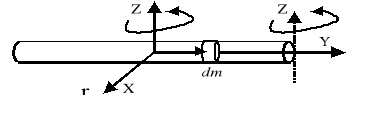
Cienki jednorodny pręt o gęstości liniowej
![]()
i długości l.
Obrót wokół osi Z:
![]()
oraz ![]()
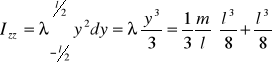
czyli ![]()
Jeżeli oś obrotu jest przesunięta do Z' o ![]()
:
wówczas z twierdzenia Steinera: ![]()
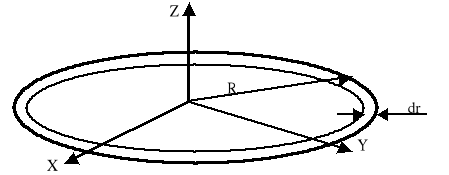
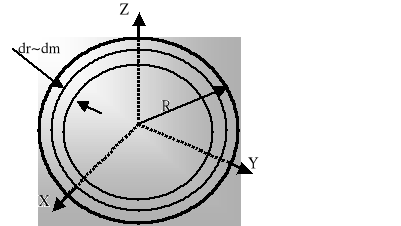
Powierzchniowy rozkład masy.
Cienki jednorodny dysk o promieniu R i gęstości powierzchniowej
![]()
![]()
![]()
![]()
gdzie ds=2πrdr
więc 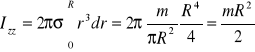
pozostałe momenty bezwładności - korzystając z własności ciała o symetrii osiowej:
Dla ogólnego przypadku: ![]()
gdzie ![]()
a więc ![]()
![]()
Dla rozważanego dysku gdy ![]()
otrzymujemy:
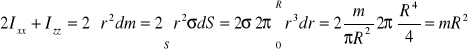
Tak więc ![]()
stąd ![]()
Lub obliczając inaczej - skoro x2+ y2+ z2 =r2 oraz x = y a więc r2= 2x2
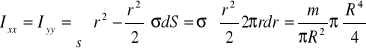
![]()
Powłoka kulista.
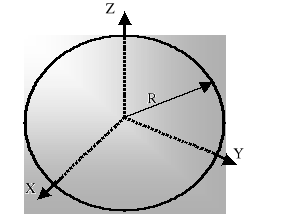
Gęstość powierzchniowa powłoki o promieniu R wynosi ![]()
Skoro jest symetria kulista to:
![]()
![]()
czyli ![]()
Lub obliczając inaczej:
Skoro x2+ y2+ z2 =r2 oraz x = y= z a więc r2= 3x2
Więc ![]()
czyli 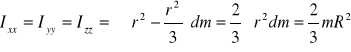
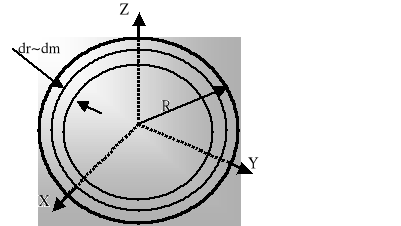
4. Objętościowy rozkład masy.
Kula o promieniu R i gęstości objętościowej ρ.
![]()
skoro 3x2= r2 ![]()
więc ![]()
![]()
ponieważ ![]()
więc ![]()
stąd po podstawieniu:
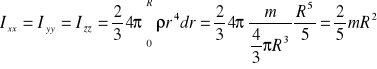
różne od zera tylko
wartości osi głównych
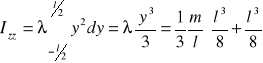
Wyszukiwarka
Podobne podstrony:
1491
1491
1491
1491 W7 Kratownice 2012(1)
1491
1491 ?z ciebie znikam ira QI3QHZ32VY7PWJ3ZWXOBXZITD7O3EE67EDWQFPI
1491
św Ignacy Loyola (1491 1556)(1)
the ottoman and maluk war1485 1491
Św Ignacy Loyola (1491 1556 ) życie i dzieło
więcej podobnych podstron