1. Elementy logiki

Ćwiczenia

Zadanie 1. Stwierdź, czy podane wyrażenia są zdaniami logicznymi. Dla zdań logicznych podaj ich wartość logiczną.

a )Każda liczba rzeczywista jest kwadratem innej liczby rzeczywistej.

b) Istnieje liczba naturalna x taka, że
.

c)
.

d) Czy 2 jest liczbą pierwszą?

e) Dla każdej liczby naturalnej x zachodzi
.

Zadanie 2. Oceń wartość logiczną zadań:

a)
;

b)
;

c)
(zapis 6|30 oznacza, że 6 jest podzielnikiem 30);

d)
;

e)
, (zapis
oznacza, że 3 jest podzielnikiem 10);

f)
;

g)
;

h)
;

i)
.

Zadanie 3. Zapisz poniższe zdania za pomocą symboli logicznych

a) Jeżeli skończę studia, to znajdę pracę albo wyjadę za granicę.

b) Nieprawda, że jeżeli zjem ciastko, to mam wyrzuty sumienia.

c) Jeżeli skończę studia, to o ile nie znajdę pracy, to wyjadę za granicę.

d) Jeżeli dziekanem zostanie profesor X to wzrośnie dyscyplina i spadnie ilość studentów, ale jeśli dziekanem zostanie profesor Y lub profesor Z, to dyscyplina nie wzrośnie i przez 2 lata będzie bałagan, albo za rok będą nowe wybory..

e) Jeżeli zdam egzamin, to wyjadę na narty, ale gdybym go nie zdała, to przełożę wyjazd na później.

Zadanie 4. Dane są zdania

p: Każdy kwadrat jest rombem, q: Każdy romb jest kwadratem.

Odczytaj i oceń wartość logiczną zdań:

.

Zadanie 5. Dane są wyrażenia:

p = „liczba naturalna x jest równa kwadratowi pewnej liczby naturalnej”,

q = „liczba naturalna x jest parzysta”,

r = „liczba naturalna x jest równa 25”.

Odczytaj następujące wyrażenia:

a)

b)
;

c)
;

d)
;

e)
;

f)
.

Zadanie 6. Dane są zdania:

p = „wielościan jest graniastosłupem prawidłowym”,

q = „przynajmniej dwie ściany wielościanu leżą w płaszczyznach równoległych”,

r = „przynajmniej dwie ściany wielościanu są wielokątami przystającymi”.

Zapisz przy użyciu powyższych oznaczeń i symboli logicznych zdania:

a) „Przynajmniej dwie ściany wielościanu leżą w płaszczyznach równoległych i przynajmniej dwie ściany wielościanu są wielokątami przystającymi”.

b) „Jeżeli wielościan jest graniastosłupem prawidłowym, to przynajmniej dwie ściany wielościanu leżą w płaszczyznach równoległych”.

c) „Wielościan jest graniastosłupem prawidłowym wtedy i tylko wtedy, gdy przynajmniej dwie ściany tego wielościanu leżą w płaszczyznach równoległych i przynajmniej dwie ściany są wielokątami przystającymi”.

d) „Wielościan jest graniastosłupem prawidłowym i nieprawda, że przynajmniej dwie ściany tego wielościanu leżą w płaszczyznach równoległych”.

e) „Jeżeli żadne dwie ściany wielościanu nie leżą w płaszczyznach równoległych lub żadne dwie ściany wielościanu nie są wielokątami przystającymi, to wielościan nie jest graniastosłupem prawidłowym”.

Zadanie 7. Oceń wartość logiczną poniższych zdań , a następnie zapisz ich zaprzeczenia.

a) „Liczba 15 jest liczbą nieparzystą i jest liczbą pierwszą”.

b) „Kwadrat jest równoległobokiem lub trapezem”.

c) „Funkcja
jest ciągła i różniczkowalna”.

d) „Jeżeli trójkąt o bokach a, b, c jest prostokątny, to
”.

e) „Jeżeli funkcja jest ciągła, to jest różniczkowalna i rosnąca”.

Zadanie 8. Rozwiąż nierówność
używając poprawnego zapisu logicznego.

Zadanie 9. Podaj sformułowania słowne poniższych zdań i oceń ich wartość logiczną.

a)
; j)
;

b)
; k)
;

c)
; l)
;

d)
; m)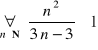
;

e)
; n)
;

f)
; o)
;

g)
; p)
;

h)
; r)
.

i)
;

Zadanie 10. Zapisz poniższe zdania za pomocą kwantyfikatorów i symboli matematycznych:

a) „x jest liczbą parzystą”;

b) ”x przy dzieleniu przez 5 daje resztę 1 lub 2”;

c) „Nie istnieje największa liczba naturalna”;

d) „Funkcja f ma dokładnie jedno miejsce zerowe”;

e) „x nie jest kwadratem żadnej liczby rzeczywistej”.

Zadanie 11. Oceń wartość logiczną podanych zdań i znajdź ich zaprzeczenia:

a)
;

b)
;

c)
;

d)
.

Zadanie 12. Podaj zaprzeczenia poniższych zdań i oceń ich wartość logiczną:

a) „każdy prostokąt jest trapezem”;

b) „każda funkcja różnowartościowa jest monotoniczna”;

c) „istnieje trójkąt równoramienny, który jest rozwartokątny lub prostokątny”;

d) „istnieje pięciokąt, na którym nie można opisać okręgu”;

e) „każda liczna naturalna jest podzielna przez pewną liczbę pierwszą”;

f) „istnieje najmniejsza liczba rzeczywista”.

Odpowiedzi

Zadanie 1.

a) - F.

b) - T.

c) - nie jest zdaniem logicznym.

d) - nie jest zdaniem logicznym.

e) - F.

Zadanie 2.

a) - T. d) - T. g) - F.

b) - T. e) - T. h) - T.

c) - F. f) - T. i) - T.

Zadanie 3.

a)
. d)
.

b)
. e)
.

c)
.

Zadanie 6.

a)
. d)
.

b)
. e)
.

c)
.

Zadanie 7.

a) - F;
. d) - F;
.

b) - T;
. e) -F;
.

c) - F;

Zadanie 8.

Zadanie 9.

a) „Istnieje taka liczba rzeczywista x, że
”; (T).

b) „Istnieje taka liczba rzeczywista x, że
”; (T).

c) „Dla każdej liczby rzeczywistej x takiej, że
zachodzi
”; (T).

d) „Dla każdej liczby rzeczywistej x istnieje taka liczba rzeczywista y, że
”; (F).

e) „Dla każdej liczby rzeczywistej x zachodzi
”; (F).

f) „Istnieje taka liczba rzeczywista x, że
”; (F).

g) „Dla każdej liczby rzeczywistej x, jeżeli
, to
”; (F).

h) „Istnieje taka liczba naturalna n, że
i n jest niewiększe niż 2”; (F).

i) „Dla każdej liczby rzeczywistej x, x jest liczbą niedodatnią lub x jest liczbą dodatnią”; (T).

j) „Dla każdych liczb rzeczywistych x i y, jeżeli
, to
lub
”; (T).

k) „Dla każdych trzech liczb rzeczywistych x, y, z, jeżeli
i liczba z jest dodatnia, to
”; (T).

l) „Dla każdej liczby naturalnej n zachodzi nierówność
”; (T).

m) „Dla każdej liczby naturalnej n zachodzi nierówność
”; (F).

n) „Istnieje taka liczba rzeczywista dodatnia x, że
”; (T).

o) „Dla każdej liczby rzeczywistej x zachodzi nierówność
”; (F).

p) „Dla każdej liczby rzeczywistej x zachodzi nierówność
”; (F).

r) „Istnieje taka liczba rzeczywista x, że
”; (T).

Zadanie 10.

a)
;

b)
lub
;

c)
;

d)
;

e)
lub
.

Zadanie 11.

a) F;
. b) F;
.

c) T;
. d) F;
.

Zadanie 12.

a) „Istnieje prostokąt, który nie jest trapezem” (T).

b) „Istnieje funkcja różnowartościowa, która nie jest monotoniczna” (T).

c) „Każdy trójkąt równoramienny jest rozwartokątny i prostokątny” (F).

d) „Na każdym pięciokącie można opisać okrąg” (F).

e) „Istnieje taka liczba naturalna, która nie jest podzielna przez żadną liczbę pierwszą” (T).

f) „Dla każdej liczby rzeczywistej istnieje liczba rzeczywista od niej mniejsza; lub - nie istnieje najmniejsza liczba rzeczywista” (T).

---