Wykład 20

20. Elektrostatyka II

1. Obliczanie potencjału

Rozważmy np. różnicę potencjałów (napięcie) pomiędzy środkiem i powierzchnią naładowanej powłoki kulistej.

Ponieważ E = 0 (wzdłuż drogi całkowania) więc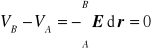
tzn. w środku i na powierzchni jest ten sam potencjał.

Z powyższego wzoru wynika, że

(20.1)

Przykład 1

Obliczyć potencjał V i pole E w odległości r od dipola ustawionego wzdłuż osi x. Moment dipolowy p = qL i dodatkowo r >> L.

Jeżeli r >> L to punkt P jest odległy od ładunku +q o:

[r - (1/2)Lcosθ]

oraz od -q o:

[r + (1/2)Lcosθ]

Całkowity potencjał jest sumą

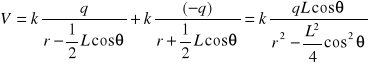
Dla r >> L otrzymujemy ostatecznie

Teraz rozpatrzmy pole i różnicę potencjałów dla dwóch przeciwnie naładowanych płyt o polu powierzchni S znajdujących się w odległości d od siebie. Jeżeli ładunki na płytach wynoszą odpowiednio +Q i -Q to gęstości ładunków wynoszą Q/S i -Q/S.

ΔV = - Ed

Zgodnie z naszymi obliczeniami

ΔV = σd/ε₀

(20.2)

Na zakończenie zaznaczmy, że powierzchnia każdego przewodnika jest powierzchnią stałego potencjału (powierzchnią ekwipotencjalną).

2. Pojemność

Kondensator - układ przewodników, który może gromadzić ładunek elektryczny.

Definicja pojemności

(20.3)

Jednostka farad. 1F = 1C/1V.

Powszechnie stosuje się μF, nF, pF.

Dla kondensatora płaskiego na podstawie (20.3) i (20.2)

(20.4)

3. Energia pola elektrycznego

Początkowo nie naładowany kondensator ładuje się od 0 do napięcia U. Wtedy ładunek wzrasta od 0 do Q, gdzie Q = CU.

Praca zużyta na przeniesienie ładunku dq z okładki "-" na "+" wynosi

dW = Udq

Całkowita praca wynosi więc

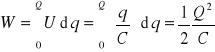
(20.5)

Dla kondensatora płaskiego

Podstawiamy to do wzoru na energię i otrzymujemy

Podstawiając wyrażenie na C dostajemy

Sd - objętość kondensatora, więc gęstość energii w = W/Sd

(20.6)

Jeżeli w jakimś punkcie przestrzeni jest pole E to możemy uważać, że jest tam zmagazynowana energia w ilości
na jednostkę objętości.

4. Dielektryki

Rozważaliśmy pole elektryczne od przewodników w próżni.

Stwierdzamy, że umieszczenie materiału nieprzewodzącego (dielektryka) między okładkami kondensatora powoduje zwiększenie pojemności od wartości C do wartości C'.

gdzie κ jest względną przenikalnością elektryczną (stałą dielektryczną).

1. Dielektryki, pogląd atomistyczny

Dwie możliwości:

• cząsteczki polarne np. H₂O mające trwałe momenty dipolowe p

• cząsteczki (atomy) mają indukowany (przez zewnętrzne pole E) moment dipolowy (przykład z atomem wodoru - Wykład 19).

Przykład 2

Atom wodoru umieszczony w zewnętrznym polu E₀.

Siła F = - eE₀ przesuwa chmurę elektronową o x₀ względem rdzenia (protonu). Wówczas atom ma moment indukowany p = ex₀.

Pole w miejscu protonu

E = E₀ + E_chmura

Ponieważ proton (rdzeń) w położeniu równowagi więc E = 0, skąd dostajemy

Indukowany moment dipolowy jest zatem równy

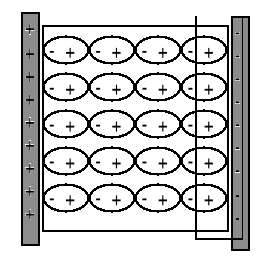
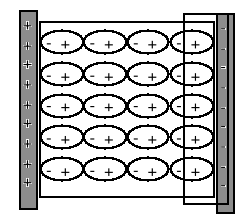
Elektryczne momenty dipolowe p dążą do ustawienia zgodnie z kierunkiem pola, a momenty indukowane są równoległe do pola. Materiał w polu E zostaje spolaryzowany (rysunek).

W rezultacie dodatni ładunek gromadzi się na jednej, a ujemny na drugiej powierzchni dielektryka. Wewnątrz nie pojawia się żaden ładunek. Indukowany ładunek powierzchniowy q' pojawia się więc gdy dielektryk umieścimy w polu elektrycznym.

Wybieramy powierzchnię Gaussa (linia przerywana).

ES=(q - q')/ε₀

E = (q - q')/(ε₀S)

Pojemność takiego kondensatora

Dzieląc przez C otrzymamy

1. Dielektryki - rozważania ilościowe.

Jeżeli każda cząsteczka ma średni moment dipolowy
skierowany zgodnie z polem E i jeżeli w dielektryku jest N cząsteczek to całkowity moment dipolowy p_całk = N

Z drugiej strony ładunek (indukowany) jest na powierzchni więc

p_całk = q'd

Łącząc te wyrażenia

q'd = N

q'd = (nSd)

gdzie n jest ilością cząsteczek w jednostce objętości.

q' = nS

Podstawiamy to do wzoru na κ

Obliczyliśmy, że

Podstawiając E = (q - q')/(ε₀S)

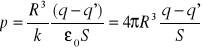
Wstawiając to do wyrażenia na κ

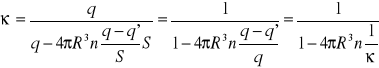
Obliczamy κ

κ = 1 + 4πnR³

1. Trzy wektory elektryczne

Przypomnijmy, że: E₀ = q/ε₀S

Pokazaliśmy, że wprowadzenie dielektryka zmniejsza pole elektryczne (indukowany ładunek daje pole przeciwne do E₀)

E = (q - q')/(ε₀S) lub E = E₀/κ = q/(ε₀Sκ)

Łącząc te równania dostajemy

Mnożąc przez ε₀ i przenosząc wyrazy otrzymujemy

Przepisujemy to równanie w postaci

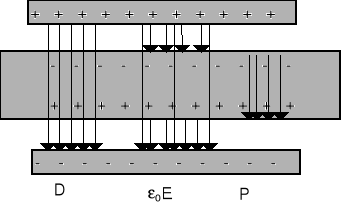
D = ε₀E + P (20.8)

D, E, P są wektorami odpowiednio: indukcji elektrycznej, natężenia pola, polaryzacji.

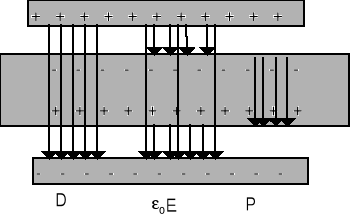
Na rysunku pokazane są odpowiednie wektory.

D - ładunek swobodny

ε₀E - wszystkie ładunki

P - ładunek polaryzacyjny

Z. Kąkol-Notatki do Wykładu z Fizyki

19-8

20-6

---