Definicja
Superpozycją (złożeniem) odwzorowanie f:X→Y i g:Y→Z nazywamy takie odwzorowanie g°f:X→Z , które spełmia warunek ∀x∈X (g°f)(x)=g[f(x)]
Definicja
Odwzorowanie f:X→Y nazywamy odwracalnym, jeżeli istnieje taka funkcja g:Y→X, Ze spełnione są warunki: f°g=idy ∧ g°f=idx (id![]()
X→X:id(x)=x).
Odwzorowanie odwrotne do odwzorowania f oznaczamy f![]()
∀x∈X f![]()
[f(x)]=x i ∀y∈Y f![]()
[f(y)]=y .Odwzorowanie f jest odwracalne ⇔ gdy jest bijekcją.
Definicja
Jeżeli spełniony jest warunek ∃e∈A ∀a∈A e#a=a#e=a to element e nazywamy elementem neutralnym, a półgrupę - półgrupą unitarną.
Definicja
Półgrupę unitarną komutatywną, w której każdy element ma element symetryczny, tzn. ∀A ∃a'∈A a#a'=a'#a=e nazywamy grupą abelową.
Definicja
Trójką (A,#,°)[gdzie #,°-dwa działania wewnętrzne w niepustym zbiorze A] spełniającą warunki:
1.para (A,#)- jest grupą abelową
2.para (A,°)- jest półgrupą
3. działanie „°” jest dystrybutywne ( rozdzielne ) względem działania „#” tzn. ∀a,b,c∈A (a#b)°c=(a°c)#(b°c) c°(a#b)=(c°a)#(c°b) nazywamy pierścieniem.
Definicja ciała
Pierścień całkowity, w którym każdy element niezerowy ma element symetryczny (względem drugiego działania) nazywamy ciałem. Elementy ciała nazywamy liczbami albo skalarami.
Definicja przestrzeni liniowej (wektorowej)
Niech V=(A,+) [będzie grupą abelową], K dowolnym ciałem zaś S:K×V→V odwzorowaniem, które parze elementów (α,V)∈ K×V będziemy oznaczać S(α,V)=αV. Trójkę (V,K,S), która spełnia warunki:
1.∀α∈K ∀a,b,c∈V α(a+b)=αa+αb
2.∀α,β∈K ∀a∈V (α+β)a=αa+βa
3.∀α,β∈K ∀a∈V (αβ)a=α(βa)
4.∀a∈V 1a=a - nazywamy przestrzenią liniową, przestrzenią wektorową nad ciałem K i oznaczamy symbolem V(K). Elementy grupy V nazywamy wektorami, a odwzorowanie S, mnożeniem skalarów przez wektory.
Definicja
Kombinacją liniową n wektorów a![]()
,a![]()
,...,a![]()
z przestrzeni wektorowej [∈V(K)] o współczynnikach ![]()
nazywamy element przestrzeni V postaci
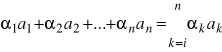
.
Definicja
Wektory a![]()
,a![]()
,...,a![]()
∈V(K) są liniowo zależne ⇔ gdy przynajmniej jeden z nich da się przedstawić jako kombinacja liniowa pozostałych.
Dowód:
Wektory a![]()
,a![]()
,...,a![]()
są liniowo zależne ⇒ ![]()
ale istnieje α![]()
≠0 ⇒ ![]()
=![]()
⇒ ![]()
⇐wynika, że jeden z wektorów da się przedstawić jako kombinacja pozostałych.⇐ ![]()
⇒![]()
. Kombinacja jest nietrywialna ponieważ β![]()
=-1≠0, czyli wektory są liniowo zależne.
Definicja
Bazą przestrzeni liniowej V(K) nazywamy niepusty jej podzbiór, którego wektory e![]()
są liniowo niezależne, przy czym każdy wektor V da się przedstawić w postaci kombinacji liniowej wektorów bazy. Ilość elementów w bazie nazywamy wymiarem przestrzeni i oznaczamy symbolem dimV. ∀∋a=![]()
- rozkład wektora w bazie {e![]()
}
Liczby zespolone
Twierdzenie 1
Jeżeli liczby zespolone z i z' są różne od zera, a ϕ![]()
i ϕ![]()
są dowolnymi argumentami tych liczb, to suma ϕ![]()
+ϕ![]()
jest argumentem iloczynu zz' zaś różnica ϕ![]()
-ϕ![]()
jest argumentem ilorazu ![]()
Twierdzenie 2 (wzory Moivre'a)
Jeżeli liczba zespolona z jest różna od zera, a ϕ jest jej dowolnym argumentem, to liczba rzeczywista nϕ , gdzie n∈N , jest argumentem liczby z![]()
.
(cosϕ+isinϕ)![]()
=cosnϕ+isinnϕ
z![]()
=|z|![]()
( cosnϕ+isinnϕ)
Twierdzenie
Jeżeli z≠0 i z=|z|(cosϕ+isinϕ), to ![]()
jest zbiorem n-elementowej postaci:
![]()
=![]()
; k=0,1,2,...,n-1
Twierdzenie Bezouta
Jeżeli z![]()
jest miejscem zerowym wielomianu p, to wielomian ten jest podzielny przez dwumian z- z![]()
i odwrotnie, czyli p(z)=0 ⇔ (z- z![]()
)|p(z).
Twierdzenie d'Alamberta
Każdy wielomian w dziedzinie zespolonej stopnia n≥1 ma co najmniej jedno miejsce zerowe.
Wielomiany w liczbie zespolonej
Twierdzenie
Jeżeli liczba zespolona z![]()
jest pierwiastkiem wielomianu p o wspólczynnikach rzeczywistych, to również pierwiastkiem tego wielomianu jest liczba sprężona ![]()
.
Funkcje wymierne
Twierdzenie
Każdą funkcję wymierną właściwą ![]()
można przedstawić w postaci sumy pewnej liczby ułamków prostych, przy czym:
1.Każdemu czynnikowi postaci (x- x![]()
)![]()
w rozkładzie mianownika q na czynniki odpowiadają w tej sumie składniki :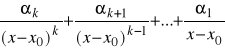
; gdzie α![]()
...α![]()
∈R
2.Każdemu czynnikowi postaci (x![]()
+bx+c)![]()
w rozkładzie mianownika q na czynniki odpowiadają w tej sumie składniki: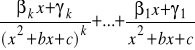
gdzie ![]()
b,c∈R oraz b![]()
-4c<0
Macierze i wyznaczniki
Definicja macierzy
Macierzą wymiaru m×n nazywamy wartość odwzorowania, którego dziedziną jest iloczyn kartezjański {1,2,...,m}×{1,2,...,n} a wartości są z pewnego zbioru (ciała) K : {1,2,...,m}×{1,2,...,n}→a![]()
∈K
Definicja
Wyznacznikiem macierzy kwadratowej A![]()
nazywamy wartość odwzorowania det:![]()
zbioru macierzy stopnia n, które spełnia warunki :
1.jednorodność ![]()
∀λ∈K det(a![]()
,...,λa![]()
,...,a![]()
)=λ(a![]()
,...,a![]()
,...a![]()
)
2.addytywność ![]()
det![]()
=det![]()
+det![]()
3.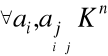
det![]()
=-det![]()
4.detE=det
=1 E- macierz jednostkowa
Własności:
1.detA=detA![]()
wszystkie własności sformułowane dla kolumn są prawdziwe dla wierszy.
2.det(0![]()
)=0 z własności 1.
3.Pomnożyć wyznacznik przez liczbę, znaczy pomnożyć 1 kolumnę macierzy przez tę liczbę.
4.Zamiana miejscami dwóch kolumn macierzy powoduje zmianę znaku wyznacznika.
5.Macierz o dwóch identycznych kolumnach ma wyznacznik równy 0 lub macierz o dwóch kolumnach proporcjonalnych ma wyznacznik równy zero.
det![]()
=-det![]()
detA=0
6.Macierz o kolumnie zerowej ma wyznacznik równy 0 det![]()
=det![]()
= det![]()
+(-1)det![]()
=0
7.Jeżeli w macierzy jedna kolumna jest kombinacją liniową pozostałych kolumn, to wyznacznik macierzy równa się zero det![]()
= =det![]()
+det![]()
+...+det![]()
=0
8.Wyznacznik macierzy nie zmieni wartości, Jeśli do jego dowolnej kolumny dodamy kombinację liniową pozostałych.
9.Wyznacznik macierzy jest równy 0⇔, gdy kolumny tej macierzy są liniowo zależne.
10.(twierdzenie Cauchy'ego)-Wyznacznik iloczynu macierzy równy jest iloczynowi wyznaczników macierzy. det(A*B)=(detA)*(detB)
jeśli AB#BA det(AB)=det(BA)
Definicja minora
Minorem M![]()
elementu a![]()
macierzy A nazywamy wyznacznik macierzy, którą otrzymamy usuwając z macierzy A i-ty wiersz i j-tą kolumnę.
Definicja
Dopełnieniem algebraicznym A![]()
elementu a![]()
macierzy A nazywamy liczbę określoną wzorem A![]()
:=(-1)![]()
M![]()
Definicja
Macierz kwadratową A nazywamy macierzą nieosobliwą jeśli jej wyznacznik jest różny od 0; jeśli detA=0, to A nazywamy macierzą osobliwą.
Definicja
Jeżeli macierze A,B∈![]()
oraz AB=BA=E to macierz B nazywamy odwrotną do macierzy A i oznaczamy ją symbolem A![]()
.
Twierdzenie
Macierz A ma macierz odwrotną ⇔ gdy jest macierzą nieosobliwą.
Dowód: ⇒istnieje A![]()
⇒AA![]()
=A![]()
A=E⇒(twierdzenie Cauchy'ego) det (AA![]()
)=detE=1 (detA)(detA![]()
)=1⇒detA≠0⇒A jest nieosobliwa
⇐ A jest nieosobliwa ⇒ detA≠0⇒można zdefiniować B=![]()
A![]()
AB=A=![]()
A![]()
=![]()
AA![]()
. Wniosek 3 z tw Laplace'a mówi, że ![]()
AA![]()
=![]()
(detA)*E=E BA=![]()
A![]()
A=![]()
(detA)*E=E
Macierz B jest macierzą odwrotną do macierzy A.
Definicja
Niech U i V będą przestrzeniami liniowymi nad tym samym ciałem K. Odwzorowanie f:U→V spełniające warunki:
1.∀a,b∈U f(a+b)=f(a)+f(b) - addytywność odwzorowania
2.∀λ∈K ∀a∈U :f(λa)=λf(a) - jednorodność odwzorowania - nazywamy przekształceniem liniowym przestrzeni U w V
i 2.)⇔ ∀λ
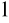
,λ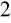
∈K ∀a,b∈U f(λ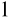
a+λ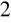
b)=λ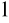
f(a)+λ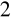
f(b)
Jeśli V=R to przekształcenie nazywamy formą liniową. F(U) podprzestrzeń liniowa przestrzeni V.
Twierdzenie Cramera.
Jeżeli macierz podstawowa A układu n równań z n niewiadomymi jest macierzą nieosobliwą, to istnieje dokładnie jedno rozwiązanie układu równań dane wzorami:![]()
;i=1,...,n lub x=A![]()
b
Dowód:detA![]()
=det(a![]()
,...,a![]()
,b,a![]()
,...,a![]()
)=det(a![]()
,...,a![]()
,x![]()
a![]()
+x![]()
a![]()
+...+x![]()
a![]()
,a![]()
,...,a![]()
)= x![]()
det(a![]()
,a![]()
,...,a![]()
,a![]()
,a![]()
,...,a![]()
)+x![]()
det(a![]()
,a![]()
,...,a![]()
,a![]()
,a![]()
,...,a![]()
)+..+ x![]()
det(a![]()
,a![]()
,...,a![]()
,a![]()
,a![]()
,...,a![]()
)+ x![]()
det(a![]()
,a![]()
,...,a![]()
,a![]()
,a![]()
,...,a![]()
)
detA![]()
=x![]()
detA⇒ x![]()
=![]()
bo detA≠0
Wniosek:
Jednorodny układ Cramerowski ma tylko rozwiązanie zerowe.
Definicja rzędu macierzy.
Rzędem niezerowej macierzyA=( a![]()
,a![]()
,...,a![]()
) nazywamy ilość liniowo niezależnych wierszy bądź kolumn tych macierzy.
Uwaga 1: Rzędem macierzy A nazywamy największy stopień jej minora różnego od 0.
Uwaga 2: DimL=( a![]()
,a![]()
,...,a![]()
)=r(A)
Własności rzędu macierzy:
1.r(A)=0⇔ A=0
2.r(A)=r(A![]()
)
3.r(A)≤min(m,n) jeśli A∈![]()
4.Rząd macierzy nie zmieni się jeśli dokonamy na kolumnach tej macierzy operacji, które nie zmienią wartości wyznacznika. W szczególności rząd macierzy nie zmieni się jeśli usuniemy z niej kolumnę zerową, lub z dwóch kolumn proporcjonalnych usuniemy jedną.
Twierdzenie Kroneckera-Capelliego
Ukłąd równań liniowych Ax=B posiada co najmniej jedno rozwiązanie ⇔r(A)=r(A![]()
)
Dowód:
Układ (![]()
) jest rozwiązaniem ⇔ ![]()
⇔ b∈( a![]()
,a![]()
,...,a![]()
) ⇔L(a![]()
,a![]()
,...,a![]()
)=L(a![]()
,a![]()
,...,a![]()
,b)⇔dim(a![]()
...a![]()
)=dim(a![]()
...a![]()
,b) ⇔r(A)=r(A![]()
)
Podsumowanie:
1.r(A)=r(A![]()
)=n-ilość niewiadomych-jedno rozwiązanie
2. r(A)=r(A![]()
)=k<n-nieskończenie wiele rozwiązań zależnych od n-k parametrów.
3. r(A)≠r(A![]()
)-układ sprzeczny-brak rozwiązań
Przestrzeń metryczna i unormowana
Definicja:
Odwzorowanie d:A![]()
→R , gdzie A≠0 spełniające warunki :
1.∀a,b∈A d(a,b)=0⇔ a=b
2.∀a,b∈A d(a,b)=d(b,a) - symetria
3.∀a,b∈A d(a,b)≤d(a,c)+d(c,b)-nierówność trójkątna - nazywamy metryką w zbiorze A. Wartość tego odwzorowania na parze elementów (a,b)nazywamy odległością elementów a i b.
∀a,b∈A d(a,b)≥0
d(a,b)=![]()
[ d(a,b)+d(b,a)]≥ ![]()
d(a,a)=0
Definicja
Przekształcenie f:A→A gdzie (A,°) przestrzeń metryczna, spełniające warunek:
∀a,b∈A d(f(a),f(b))=d(a,b) nazywamy izometrią.
Definicja
Przekształcenie f:A→A gdzie (A,°) przestrzeń metryczna, spełniające warunek:
∃λ∈(0,1) ∀a,b∈A d(f(a),f(b))≤λd(a,b) nazywamy przekształceniem zwężającym lub kontrakcją.
Przestrzeń unormowana
Niech V (przestrzeń liniowa) nad ciałem R. Funkcjonał (odwzorowanie) ||•||:V→R spełniająca warunki:
1.∀v∈V ||v||=0 ⇔ v=0
2.∀λ∈R ∀v∈V ||λv||=|λ|*||v||
3.∀v![]()
,v![]()
∈V ||v![]()
+v![]()
||≤||v![]()
||+||v![]()
|| nazywamy normą w przestrzeni V, a przestrzeń liniową z określoną normą nazywamy przestrzenią unormowaną.
Definicja iloczynu skalarnego
Niech V będzie przestrzenią liniową nad ciałem R, odwzorowanie g: V![]()
→R spełniające warunki:
1.∀x,y,z∈V g(x+y,z)=g(x,z)+g(y,z) g(x,y+z)=g(x,y)+g(x,z)
2.∀x,y,z∈V ∀λ∈R g(λx,y)=g(x,λy)=λg(x,y) - odwzorowanie jest liniowe
3.∀(x,y)∈V g(x,y)=g(y,x)
4.∀x≠0 g(x,x)>0 nazywamy mnożeniem skalarnym w przestrzeni V, a wartość tego odwzorowania na wektorach (![]()
) nazywamy iloczynem skalarnym tych wektorów x°y=|![]()
| |![]()
| cosϕ . Przestrzeń liniowa, w której wprowadzono iloczyn skalarny nosi nazwę przestrzeni unitarnej.
Własności iloczynu skalarnego:
1.∀x,y∈V |x+y|≤|x|+|y| - nierówność Minkowskiego
2.∀x,y∈V |x*y|≤|x|*|y| - nierówność Coshy-Buniakowskiego.
Dowód:
λ∈R (λx+y)(λx+y)=λ![]()
x![]()
+2λxy+y![]()
≥0 dla każdego x
Δ≤0 Δ=(2x°y)![]()
-4x![]()
y![]()
=4((x°y)![]()
- x![]()
y![]()
)≤0
(x°y)![]()
≤ x![]()
y![]()
|x°y|≤|x| |y|
3.![]()
4.![]()
, α∈R 5.![]()
Definicja iloczynu wektorowego
Mnożeniem wektorowym w R![]()
nazywamy odwzorowanie f:R![]()
×R![]()
→R![]()
spełniające warunki:
1.∀a,b∈R![]()
a×b=-b×a
2.∀a,b,c∈R![]()
a×(b+c)=a×b+a×c (a+b)×c=a×c+b×c
3.∀λR∈ ∀a,b∈R![]()
(λa)×b=a×(λb)=λ(a×b)
4.![]()
![]()
![]()
Własności:
1.Jeśli wektory a,b są kolinearne to ![]()
∃λ∈R b=λa
![]()
ale z war.1. ![]()
2. Wektory a i b są ortogonalne do wektorów a×b ![]()
Iloczyn mieszany
Iloczynem mieszanym uporządkowanej trójki wektorów a,b,c nazywamy liczbę określoną wzorem: abc=a°(b×c).
Własności:
1.![]()
2.Trzy niezerowe wektory a,b,c są współpłaszczyznowe (komplementarne) jeśli abc=0
3. Jeśli a,b,c∈R![]()
a,b,c=det(a,b,c)
4.det(a,b,c) jest równy objętości równoległościanu rozpiętego na wektorach a,b,c
Definicja powierzchni stopnia II
Zbiór punktów (x,y,z)∈R![]()
, których współrzędne spełniają zależność :
![]()
gdzie:
![]()
nazywamy powierzchnią stopnia II lub kwadrykiem.
Wyszukiwarka
Podobne podstrony:
sciaga algebra wzory, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geometrią
sciaga algebra dowody, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geometri
sciaga algebra dowody 1, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geomet
sciaga algebra definicje, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geome
sciaga algebra dowody 2, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geomet
opracowane kolos, WAT- Elektronika i Telekomunikacja, Semestr I, Pnor, Pnor
zadania 2(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 9(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
Test B, WAT- Elektronika i Telekomunikacja, Semestr II, Materiały elektroniczne, kolos
WSTĘP TEORETYCZNY, WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, labfizy
Egzaminacyjne dane przez Pluta, WAT- Elektronika i Telekomunikacja, Semestr II, Elementy elektronicz
zadania 7(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
Sys kom lab harmonogram zao2015 E3, WAT- Elektronika i Telekomunikacja, Semestr V, Systemy Komutacyj
sprawozdanie-kopia, WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, labfiz
spraw fm(1), WAT- Elektronika i Telekomunikacja, Semestr V, Technika Emisji i Odbioru, laboratoria,
więcej podobnych podstron