Spis treści

1. Wstęp………………….……………..……………………………………………………………………3

2. Wykład 1………………...…………….………………………………………………………………….4

3. Wykład 2………………...…………..………………………………………………………………….5-6

4. Wykład 3………………..…………..…………………………………………………………………….7

5. Wykład 4………………………………………………………………………………………………8-10

6. Wykład 5…………..…………………………………………………………………………………11-13

7. Wykład 6……………...…………………………………………………………………………………14

8. Wykład 7…………………………………………………………………………………………….15-17

Wstęp

Witam serdecznie, na początku chciałabym podkreślić, że tytuł jest dla śmiechu, nie miałam zamiaru kogokolwiek urazić. Jeśli jednak tak się stało, to przepraszam.

W poniższym opracowaniu zamieszczam swoje odpowiedzi i wyjaśnienia dla Was jak do tego doszłam na pytania kontrolne do wykładów ze statystyki prowadzone w semestrze letnim w roku 2008 przez dr Bradtke, które znajdują się na stronie instytutu pod adresem: http://www.ocean.univ.gda.pl/dydaktyka/zof/kursy/Stat.htm

Pragnę podkreślić, że odpowiedzi są zazwyczaj krótkie i proste, największą trudność sprawia zrozumienie pytania.

Życzę miłej lektury.

Anna Werner

Ja od siebie tylko dodam, że oba opracowania zmieniłam tak, żeby były jeszcze bardziej zrozumiałe.

W miarę jak będą się pojawiały nowe pytania kontrolne dla naszego semestru będę je sukcesywnie dodawała do opracowania. (To obecne będzie miało roboczo wersję 1.0)

Miłej nauki

LuSy Słomska

WYKŁAD 1

1) W celu oszacowania przeciętnej wielkości omułka bałtyckiego odłowiono w sposób losowy 100 osobników, po czym określano długość muszli każdego z nich.

a) czym w badaniach jest populacja generalna, a czym próba?

Próba to zbiór wartości wielkości losowo odłowionych 100 osobników omułka bałtyckiego, a populacja to zbiór wartości wielkości wszystkich osobników omułka bałtyckiego.

b) podaj przykład statystyki i parametru

Statystyka to wartość liczbowa opisująca próbę, w tym przypadku np. średnia długość muszli 100 osobników omułka bałtyckiego (x). Parametr to wartość liczbowa liczona dla populacji, tu np. średnia długość muszli całej populacji omułka bałtyckiego (μ).

c) w jaki sposób należałoby odławiać omułki aby losowanie nazwać zależnym, a w jaki niezależnym?

Losowanie byłoby zależne, gdyby odłowiono od razu 100 osobników i zmierzono ich długość (bez zwracania), a losowanie niezależne, gdyby wyławiano po jednym osobniku, mierzono jego długość i z powrotem wrzucano do akwenu i tak 100 razy (ze zwracaniem), w tym przypadku występuje możliwość odłowienia kilkakrotnie tego samego osobnika.

2) Z jakiego rodzaju zmiennymi mamy do czynienia (jakościowe, jakościowe dychotomiczne, ilościowe interwałowe, ilościowe ilorazowe, ilościowe porządkowe) gdy analizujemy:

a) zbiór wyników pomiaru kierunków wiatru typu W, SW, N, NW,

- ilościowe porządkowe

b) zbiór wyników pomiaru prędkości wiatru wyrażonych w [m/s],

- ilościowe interwałowe

c) zbiór wyników pomiaru temperatury wody wyrażonych w [°C],

- ilościowe

d) zbiór wyników oznaczeń gatunku odławianych organizmów.

- jakościowe

3) Jeżeli liczebność próby wynosiła 15, to przedstawiony w tabeli szereg jest szeregiem szczegółowym, rozdzielczym prostym, czy rozdzielczym skumulowanym? Jak należy interpretować wartość 5 w drugim rzędzie kolumny „częstość”?

Szereg jest szeregiem rozdzielczym skumulowanym, ponieważ w takim szeregu wartości poszczególnych przedziałów są sumowane od pierwszego wiersza do końca (lub na odwrót) i największą wartością występującą w szeregu jest liczebność próby, w tym przypadku 15=n. Wartość 5 oznacza częstość występowania cechy w przedziale [0;4), ponieważ w tym przykładzie dodawano wartości od 1 wiersza do końca, więc do wartości dla przedziału [0;2) dodano wartość dla przedziału [2;4) i tak otrzymano wartość 5 z drugiego rzędu kolumny, następnie do otrzymanej wartości dodano tą dla przedziału [4;6) i otrzymano 7 itd. Na tym polega szereg rozdzielczy skumulowany.

WYKŁAD 2

1. Jeżeli wartości zmiennej X mniejsze od średniej stanowią ponad 50% wszystkich, to rozkład tej zmiennej może być symetryczny, lewoskośny czy prawoskośny?

Prawoskośny. Ponad 50% wartości jest mniejszych od średniej czyli znajduje się po lewej stronie od średniej, po lewej stronie wykresu, więc tam występuje szczyt wykresu (moda-wartość najczęstsza) i wykres może wyglądać jak jeden z tych poniższych, czyli mieć rozkład prawoskośny.

2) Ile wynoszą mediana i kwartyl dolny dla zbioru danych: 1 2 2 4 5 6 7 8 9 10 ? (n=10)

Ze wzorów obliczamy pozycję:

- dla kwartyla dolnego 25/100*(n+1)=0,25*11= 2,75

Kwartyl dolny znajduje się w miejscu 2,75 w szeregu uporządkowanym od wartości najmniejszej do największej, czyli pomiędzy liczbą 2gą i 3cią. Obie liczby mają wartość 2, a więc kwartyl pomiędzy nimi również będzie wynosił 2. Q₁=2

- dla mediany 50/100*(n+1)=5,5

Mediana znajduje się w połowie między wartością 5tą i 6tą. W tych miejscach znajdują się liczby 5 i 6 a dokładnie w połowie znajduje się liczba 5,5. Q₂=5,5

3) Policzyć średnią arytmetyczną i odchylenie standardowe (s) dla zbioru danych

xi: 1 2 3 4 5 6 7 8 9 10 (∑xi=55; ∑(xi²)=385)

Ze wzorów na średnią x= (∑xi)/n = 55/10 = 5,5;

Na odchylenie standardowe, które jest pierwiastkiem kwadratowym z wariancji

Wariancja s²= [n*∑(xi²)-( ∑xi)²]/[n*(n-1)]=(10*385-55²)/(10*9)≈9,16

Odchylenie standardowe s≈3

4) Jakie statystyki można w przybliżeniu wyznaczyć z krzywej częstości skumulowanej wykreślonej dla próby?

Poniżej znajduje się przykład krzywej częstości skumulowanej (czerwona krzywa). Na podstawie takiej krzywej można wyznaczyć medianę (wartość środkowa czyli o częstości 50%), min, max, kwartyl dolny(25%), górny(75%), centyle(co 1%), decyle(co 10%).

5) W badaniach cechy X, na podstawie 25-cio elementowej, losowej próby określono następujące statystyki: X=100,0; Md=97,0; s=9,0; Q1=94,5; Q3=102,5 oraz wykres słupkowy częstości względnych jak na rys. obok. Które statystyki (parametryczne czy nieparametryczne) powinny być podstawą do zbudowania wykresu typu „skrzynka z wąsami” dla tej próby?

Odpowiedź na podstawie histogramu, na którym widać, że cecha x nie ma rozkładu normalnego, więc używamy statystyk nieparametrycznych: mediana, kwartyl górny, kwartyl dolny.

6) W dwóch akwenach badano zasolenie wody. Okazało się, że w obu akwenach rozkłady zasolenia były w przybliżeniu symetryczne a średnie z badanych prób wyniosły tyle samo. Współczynnik zmienności natomiast w pierwszym z akwenów wynosił 25%, a w drugim 35%. Dla którego z akwenów histogram zasolenia będzie bardziej skupiony wokół średniej?

Korzystamy ze wzoru na współczynnik zmienności V(s)=s/x *100%

- dla 1 akwenu V(s)=25%, a x₁=x_{2 ,} więc 25%=s1/x*100%

- dla 2 akwenu V(s)=35%, więc 35%=s2/x*100%

Średnie są sobie równe, więc jeśli w akwenie drugim V jest większe to oznacza, że s2>s1 odchylenie też jest większe. Odchylenie standardowe określa skupienie wartości wokół średniej, i jeśli jest mniejsze to skupienie jest większe. Odpowiedź w akwenie 1 histogram będzie bardziej skupiony wokół średniej.

WYKŁAD 3

1) Dokonano pomiarów zasięgu rozpływu wód Wisły w różnych sytuacjach. Pomiary wyrażono w [km]. Obliczono x=10,00 i s=2,00. Ile wyniosłaby średnia i odchylenie standardowe gdyby zasięg wyrażono w metrach?

Stosujemy kodowanie zmiennej: y=x*c. W efekcie mnożymy średnią i odchylenie standardowe przez stałą c: y=c*x i Sy=c*Sx.

Odpowiedź: x= 10 000m, s= 2 000m

2) Dokonano pomiaru absorbancji roztworów (o różnych stężeniach) pewnej substancji rozpuszczonej w wodzie morskiej. Dla zmierzonych wartości obliczono x=0,10 i s=0,02. Aby na podstawie pomiarów absorbancji określić stężenie badanej substancji należy od wyników pomiarów odjąć absorbancję „ślepej” próby, która wynosi 0,01. Ile wyniosłaby średnia i odchylenie standardowe gdyby zastosowano tę poprawkę do każdego z pomiarów?

Kodowanie zmiennej y=x+c lub y=x-c, więc do średniej dodajemy lub odejmujemy stałą c, a odchylenie standardowe pozostaje bez zmian y=x+c i Sy=Sx.

Odpowiedź: x=0,10-0,01=0,09, s=0,02.

3) Jeżeli interesująca nas cecha X ma rozkład normalny o średniej μ=15 i σ=1, to

a) jakie jest prawdopodobieństwo, że XЄ(13;17)?

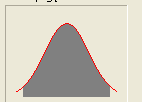
Najlepiej narysować sobie rozkład normalny ze średnią 15 i zaznaczyć przedział (13;17). Dokładnie widać, że 15-13=2 i 17-15=2, a odchylenie równe jest 1 jednostce. Aby odpowiedzieć na pytanie bez użycia kalkulatora prawdopodobieństwa wystarczy zapamiętać, że P(μ-1σ< x< μ+1σ)=68,26%

P(μ-2σ< x< μ+2σ)=95,46%

P(μ-3σ< x< μ+3σ)=99,73%

Odpowiedź 95%, ponieważ P(13<x<17)= P(μ-2σ< x< μ+2σ)=95%.

b) czy P(X<13) jest takie samo jak P(X>18)?

Odpowiedź: nie, ponieważ jest to rozkład normalny i można odczytać z wykresu, że wartość 18 znajduje się dalej od średniej niż wartość 13 i prawdopodobieństwo P(x>18) jest mniejsze niż P(x<13), czyli nie są sobie równe (18=15+3, 13=15-2)

c) które z prawdopodobieństw jest większe P(X<14), czy P(X<12)?

Odpowiedź: P(x<14), można odczytać z wykresu, że wartość 14 znajduje się bliżej średniej niż 12 i tym samym P(x<14) jest większe niż P(x<12).

4) Jeżeli zmienna losowa X ma rozkład N(μ;σ), a zmienna losowa Y ma rozkład LN(μ;σ), to jaki jest związek pomiędzy X i Y ?

X=lnY

(na ćwiczeniach często x miał rozkład lognormalny i dodawaliśmy nową zmienną y=ln(x), w tym przypadku jest tylko na odwrót: y ma rozkład lognormalny, a x=ln(y) ma rozkład normalny).

5) Czym różni się kodowanie i transformacja danych?

Kodowanie zmiennej to inaczej przeskalowanie, nie zmienia rozkładu zmiennej, polega np. na dodawaniu, odejmowaniu, mnożeniu i dzieleniu przez stałą.

Transformacja zmienia rozkład i stosujemy ją po to, aby znormalizować rozkład skośny. Przykłady transformacji w celu normalizacji rozkładu dla rozkładów prawoskośnych: pierwiastkowanie, logarytmowanie,

Dla rozkładów lewoskośnych: potęgowanie, funkcje wykładnicze.

6) Jeśli zmienna X ma rozkład prawoskośny, to zmienna Y=X^(1/3) będzie miała rozkład bardziej skośny od zmiennej X, czy bardziej symetryczny?

Pierwiastkujemy, więc rozkład prawoskośny stanie się bardziej symetryczny.( x do potęgi 1/3 to inaczej pierwiastek 3 stopnia z x)

WYKŁAD 4

1) Co oznacza efektywność i nieobciążoność estymatora?

Estymator jest najbardziej efektywny, kiedy odchylenie standardowe próby jest najmniejsze z możliwych.

Estymator jest nieobciążony, kiedy średnia próby jest najbliższa średniej populacji.

2) Czym podyktowane zostało wprowadzenie do wzoru na wariancję (s2) wyrażenia (n-1) w mianowniku?

Dzięki temu otrzymano estymator nieobciążony wariancji z populacji.

3) Od czego zależy szerokość przedziału ufności dla średniej i wariancji?

Z powyższych wzorów wynika, że szerokość przedziału ufności zależy od średniej, odchylenia standardowe i liczebności próby, oraz współczynnika ufności p.

4) W 100 losowo wybranych sytuacjach mierzono prędkość wiatru na pewnej stacji meteorologicznej. Otrzymano średnia x=12,00 m/s i wariancje s2=0,25 oraz informacje, że rozkład prędkości wiatru jest rozkładem normalnym. Jak bardzo, z prawdopodobieństwem 90%, parametry μ i σ tego rozkładu mogą być różne od statystyk uzyskanych z próby?

Aby rozwiązać to zadanie należałoby w programie statistica policzyć przedziały ufności dla średniej i odchylenia w statystykach opisowych.

5) Badając normalność rozkładu cechy na podstawie próby testem Kołmogorowa-Smirnowa należy wyznaczyć statystykę testowa Dmax. Co ta statystyka opisuje (jaka różnice, pomiędzy jakimi wielkościami)?

Opisuje maksymalną różnicę pomiędzy krzywą częstości względnej skumulowanej wyznaczoną dla próby a dystrybuantą rozkładu normalnego o parametrach μ~x i σ2~s2

6) Kiedy o różnicy mówimy, że jest istotna statystycznie, a kiedy że nie jest istotna statystycznie?

Różnica jest istotna statystycznie, kiedy występuje małe prawdopodobieństwo, że pojawiła się przypadkowo.

Różnica nie jest istotna statystycznie, kiedy występuje duże prawdopodobieństwo, że pojawiła się przypadkowo.

ZADANIE 7 I 8 ROZWIĄZUJEMY W OPARCIU O TABELĘ:

7) W 100 losowo wybranych sytuacjach mierzono prędkość wiatru na pewnej stacji meteorologicznej. Otrzymano średnia x=12,00 m/s i wariancje s2=0,25. W celu określenia czy rozkład prędkości wiatru jest rozkładem normalnym wykorzystano test Kołmogorowa-Smirnowa. Określono, że maksymalna różnica pomiędzy krzywą częstości względnej skumulowanej wyznaczoną dla próby a dystrybuantą rozkładu normalnego o parametrach μ~x i σ2~s2 wynosi 0,11. Czy na poziomie istotności 5% można przyjąć, że rozkład prędkości wiatru na tej stacji jest rozkładem normalnym?

N=100, Dmax=0,11; αgr=5%

W tabeli zestawiono wartości Dmax tylko dla prób o n <40, dla większych prób trzeba te wartości policzyć ze wzorów na końcu tabeli. Podstawiając n=100 otrzymujemy wartości 0,107 0,122 0,136 0,152 0,163.

Dmax=0,110 więc znajduje się pomiędzy wartościami 0,107 a 0,122. Wartości te odpowiadają α=20% i α=10%. Szukane αЄ(10%;20%) i jest większe od αgr, więc przyjmujemy Ho o rozkładzie normalnym prędkości wiatru.

8) Testując hipotezę o normalności rozkładu badanej cechy na podstawie próby otrzymaliśmy statystykę testu Kołmogorowa- Smirnowa równa 0,43.

a) czy na poziomie istotności 5% można przyjąć, że rozkład badanej cechy nie jest rozkładem normalnym jeżeli próba liczyła 10 pomiarów?

N=10, Dmax=0,43, αgr=5%

Z tabeli odczytujemy, że dla n=10 wartość 0,43 znajduje się pomiędzy wartościami 0,409 i 0,457. Więc α znajduje się pomiędzy 5% i 2% ( 2%< α<5%) i jest mniejsze od αgr, więc odrzucamy Ho o rozkładzie normalnym, a przyjmujemy Ha o tym, że rozkład nie jest normalny.

Odpowiedź: tak, można przyjąć, że rozkład cechy nie jest rozkładem normalnym.

b) jak duża musiałaby być próba aby taka wartość statystyki pozwoliła na odrzucenie hipotezy o normalności rozkładu badanej cechy na poziomie istotności 1%?

Aby odrzucić Ho musi być spełniony warunek α< αgr (αgr=1%). W tabeli α mniejsze od 1% znajdują się po prawej stronie od wartości 1%, więc należy odczytać dla jakiego n wartośc Dmax=0,43 również znajduje się po prawej stronie od kolumny 1%. Odpowiedź: dla n >= 14.

9) W jaki sposób można wykorzystać test Kołmogorowa-Smirnowa do zweryfikowania hipotezy, że zmienna X ma rozkład lognormalny o zadanych parametrach μ i σ dysponując próba wartości X?

Należy utworzyć nową zmienną y=ln(x) i dla niej wykonać test normalności.

Postawić hipotezy: Ho: jeśli zmienna y ma rozkład normalny, to zmienna x ma rozkład lognormalny;

Ha: jeśli zmienna y nie ma rozkładu normalnego, to zmienna x nie ma rozkładu lognormalnego;

Przyjąć αgr np. 5%. Jeśli α> αgr przyjmujemy Ho, jeśli α< αgr przyjmujemy Ha.

10) Na czym polega błąd I rodzaju, a na czym błąd II rodzaju. Dla którego z błędów jesteśmy w stanie oszacować prawdopodobieństwo jego popełnienia?

Popełniamy błąd I rodzaju kiedy odrzucamy prawdziwą hipotezę Ho, a II rodzaju gdy przyjmujemy fałszywą Ho. Jesteśmy w stanie oszacować prawdopodobieństwo popełnienia błędu I rodzaju, które wynosi α.

11) Jeśli zależy nam na przyjęciu hipotezy, że badana przez nas próba pochodzi z populacji o rozkładzie normalnym, to przy jakim poziomie istotności różnic (jak najmniejszym, czy jak największym) należy podejmować decyzję aby zminimalizować prawdopodobieństwo popełnienia błędu?

Przy jak najmniejszym, wówczas α jest jak najmniejsze.

WYKŁAD 5

1) W celu zbadania czy preferencje pokarmowe ryb występujących w pewnym akwenie wiążą się z gatunkiem analizowano treści żołądków losowo odłowionych osobników. Jako zasadniczy pokarm określano ten, którego w treści było najwięcej. Wyniki zestawiono w poniższej tablicy dwudzielczej. Uzupełnij tablice oczekiwanej liczebności osobników w każdej kategorii przy założeniu, że nie ma związku pomiędzy gatunkiem a rodzajem preferowanego pokarmu?

W tablicy dwudzielczej sumy dla poszczególnych kolumn i wierszy muszą być takie same w obu tabelach. Skoro np. dla glonów w tablicy obserwowanej suma wynosi 350, to dla glonów w tablicy oczekiwanej wartości w sumie muszą dać tyle samo. Wartości do uzupełnienia to 175 i 125.

2) O czym mówi wartość współczynnika regresji?

Współczynnik regresji znajduje się w równaniu regresji przy zmiennej x (y=ax+b) i określa o ile zmieni się zmienna zależna y kiedy zmienna niezależna x zmieni się o 1 jednostkę.

3) Kiedy błąd oceny zmiennej zależnej na podstawie równania regresji będzie rósł?

Ze wzoru BSy = PIERWIASTEK [Sy*(1-r²)] wynika, że błąd będzie rósł kiedy odchylenie standardowe będzie rosło, a współczynnik korelacji malał.

4) W dwóch akwenach (A i B) badano zależność wysokości fal (H) od prędkości wiatru przywodnego (W). Uzyskano równania regresji:

w akwenie A: HA=aA+0,5·WA w akwenie B: HB=aB+0,4·WB

W którym z akwenów wzrost prędkości wiatru o jedna jednostkę spowoduje przeciętnie większy wzrost wysokości fal?

W akwenie A, ponieważ współczynnik regresji jest większy.

5) Czy można twierdzić, że temperatura wody (T) w badanej próbie (losowej niezależnej próbie 22 pomiarów) ma związek ze średnią doza energii promieniowania padającego na powierzchnie w ciągu godziny poprzedzającej pomiar temperatury (H), na podstawie obu cech, z których uzyskano wyniki:

T [°C]: ∑T=306,1 ∑T²=4291,1

H [104 W·s/m2]: ∑H=4100 ∑H²=920088,0

∑TH=59250,6

Jeśli istnieje zależność, to jaki jest jej kierunek i siła? Obie cechy mają rozkład normalny

Aby odpowiedzieć na pytanie należy wyliczyć współczynnik korelacji. Obie cechy mają rozkład normalny, więc wyliczamy współczynnik korelacji Pearsona ze wzoru:

Nie ma znaczenia co podstawimy pod x, a co pod y. (n=22)

R=0,94 według skali zależność jest prawie pełna, a kierunek dodatni.

|r| Є (0,0 ; 0,1) nikła zależność

|r| Є [0,1 ; 0,3) słaba

|r| Є [0,3 ; 0,5) przeciętna

|r| Є [0,5 ; 0,7) wysoka

|r| Є [0,7 ; 0,9) bardzo wysoka

|r| Є [0,9 ; 1,0) prawie pełna

6) Badano spożycie tlenu (O) przez osobniki pewnego gatunku organizmów w zależności od temperatury wody (T). Obie cechy mają rozkład normalny. Z rozważań teoretycznych wiadomo, że zużycie tlenu przez te organizmy zależy od temperatury w przybliżeniu liniowo. Wyniki uzyskane w badaniach eksperymentalnych (badano spożycie przez 8 osobników):

O [j.umowne]: ∑O=342,92 ∑O^2= 16078,40 sO =21,91

T [°C]: ∑T=132,67 ∑T^2= 2350,02 sT = 8,10

∑ (T·O)= 6141,24 r = 0,997 (korelacja istotna statystycznie)

Najpierw ze wzorów wyliczamy współczynniki równania regresji y=bx+a. Ustalamy zmienną zależną-O i niezależną-T.

a) Jakiego spożycia tlenu (z prawdopodobieństwem 99,7%) należy oczekiwać w wodach o temperaturze 15°C?

Z otrzymanego równania wyliczmy O dla T=15°C, otrzymana wartość to Y obliczone.

Wyliczamy BSy ze wzoru BSy = PIERWIASTEK [Sy*(1-r² )].

1) P(Yrzecz=Yobl±1*BSy)=68%

2) P(Yrzecz=Yobl±2*BSy)=95%

3) P(Yrzecz=Yobl±3*BSy)=99,7%

Wyliczone wartości podstawiamy do 3)wyrażenia i otrzymujemy przedział wartości z prawdopodobieństwem 99,7%.

b) Jaka mogła być temperatura wód (z prawdopodobieństwem 95%), jeżeli spożycie tlenu wyniosło 50?

Podobnie jak powyżej, tylko zamieniamy zmienne y to T, a x to O. Liczymy a i b, tworzymy równanie, wyliczmy T dla O=50, wyliczmy BSy i podstawiamy do wyrażenia 2).

7) Badania prowadzone w Zatoce Gdańskiej wykazały silna zależność liniowa współczynnika osłabiania światła (c) od koncentracji masowej zawiesiny (M). Na podstawie 200 jednoczesnych pomiarów obu wielkości określono średnią koncentracje zawiesiny xM=3,5 mg/l z odchyleniem standardowym sM=1 mg/l i średni współczynnik osłabiania światła xc=2,00 m-1, z odchyleniem standardowym sc=0,50 m-1. Zarówno koncentracja zawiesiny jak i współczynnik osłabiania światła maja rozkład normalny, a współczynnik korelacji pomiędzy nimi wyniósł r=0,75 (korelacja istotna statystycznie). Jakiego współczynnika osłabiania światła, z prawdopodobieństwem 99,7%, można się spodziewać w sytuacji, gdy koncentracja zawiesin wynosi M=6 mg/l?

Podobnie jak powyżej, tylko można skorzystać z tych krótszych wzorów na a i b. (c zależy od M, czyli x-M, y-c)

8) W jakiej skali trzeba wyrazić zmienne, aby policzyć współczynnik korelacji Spearmana? W jakiej sytuacji obliczamy ten rodzaj współczynnika korelacji

Zmienne ilościowe w skali porządkowej. Obliczamy ten współczynnik, kiedy zmienne nie mają rozkładu normalnego.

9) Co jest miara siły relacji pomiędzy zmiennymi, a co jej kierunku ?

Siłę określa wartość bezwzględna ze współczynnika korelacji |r|, a kierunek znak (+) lub (-) współczynnika.

10) Co przedstawia wykres rozrzutu (diagram rozproszenia) ?

Przedstawia zależność między badanymi cechami, jej kierunek i siłę.

11) Jakiej wartości współczynnika korelacji Pearsona można się spodziewać, gdy wykres rozrzutu wygląda jak na rysunkach obok? Opisz siłę i kierunek tej zależności.

W pierwszym przypadku zależność jest prawie pełna i dodatnia r~1, w drugim przypadku r jest nieokreślone.

WYKŁAD 6

1) Kiedy należy stosować regresje liniową, a kiedy nieliniową do opisu zależności dwóch zmiennych ilościowych w skali przedziałowej lub ilorazowej?

Regresja nieliniowa jest wtedy gdy jednakowym przyrostom zmiennej niezależnej towarzyszą różne co do siły i kierunku zmiany zmiennej zależnej

Regresja liniowa jest wtedy gdy jednakowym przyrostom zmiennej niezależnej towarzyszy jednakowa co do siły kierunku zmiana zmiennej zależnej

Zależności liniowe gdy (η²-r²)~0, nieliniowe gdy (η²-r²)>1.

2) Podaj przykłady funkcji nieliniowych, dla których współczynniki dopasowania można wyznaczyć metodą regresji liniowej stosowanej do zmiennych transformowanych?

Zależności wykładnicze np. y=α*x^β

3) Jeżeli zależność pomiędzy badanymi cechami najlepiej opisuje funkcja Y=2,0·1,2^x, to jak zmieni się średnio wartość zmiennej Y gdy X wzrośnie o 1?

Należy przekształcić funkcję do postaci y=ax+b. W tym celu transformuje się poprzez logarytmowanie:

lny=ln(2,0*1,2^x)

lny=ln2,0+x*ln1,2 ln1,2=0,18

Odpowiedź: o 0,18.

4) Jaka transformacje i do której zmiennej należy zastosować, aby wykorzystać metody regresji liniowej do oszacowania parametrów dopasowania funkcji postaci Y=α·X^β?

Logarytmowanie (ln, log) zmiennej Y.

5) Jakie wyróżnia się rodzaje szeregów czasowych i czym się one różnią?

-szereg czasowy momentów(bierze się pod uwagę dany moment) „zasoby”

-szereg czasowy okresów (bierze się pod uwagę okres czasu) ”strumienie”

6) Jakie składowe zmienności wyróżnia się w szeregach czasowych?

- wahania przypadkowe, wahanie okresowe i trend

7) Czym jest trend? Jakie znasz metody wyodrębniania trendu?

Trend to długotrwała tendencja. Metody wyodrębniania trendów: metoda średnich ruchomych, metoda najmniejszych kwadratów

8) Do czego służy analiza autokorelacji?

Analiza autokorelacji służy do analizy okresowości.

9) Na czym polega wygładzanie szeregu czasowego metoda średnich ruchomych? Jaka wadę ma ta metoda (odnośnie długości szeregu wynikowego)?

Średnie ruchome wygładzają szereg nie zacierając śladów najsilniejszych wahań, dlatego też w analizie dostatecznie długich szeregów wygładzonych tą metodą można dostrzec występowanie wahań cyklicznych, najpoważniejsze wady tej metody to skracanie szeregu pierwotnego oraz trudności z wykorzystaniem jej do przewidywania poziomu badanego zjawiska w przyszłości.

WYKŁAD 7

1) Czym różnią się testy z hipoteza dwustronna i jednostronna?

Są to rodzaje hipotezy alternatywnej. Jednostronna - zakładamy konkretnie czy dana wartość jest większa czy mniejsza od drugiej, natomiast obustronna - zakładamy że wartości się różnią (ale nie zakładamy konkretnie jak się różnią). Za pomocą hipotezy Ha jednostronnej łatwiej odrzucić Ho, ponieważ α jest mniejsze.

2) W jakiej sytuacji stosuje się test Kołmogorowa-Smirnowa dla dwóch prób niezależnych, a w jakiej U-Manna Whitneya

Stosujemy test Kołmogorowa-Smirnowa, kiedy wartości często się powtarzają, natomiast test U-Manna Whitneya, kiedy powtarzają się rzadko lub wcale.

3) W jakich sytuacjach stosuje się testy parametryczne a w jakich nieparametryczne?

Testy parametryczne, kiedy cechy mają rozkład normalny, natomiast nieparametryczne, kiedy cechy nie mają rozkładu normalnego.

ZADANIA 4-10 ROZWIĄZUJEMY W OPARCIU O TABELĘ

4) Mierzono temperaturę wody (T) w dwóch akwenach (A i B). Otrzymano wyniki:

Obie próby są losowe, a rozkład temperatur w obu rejonach nie jest rozkładem normalnym. Jednocześnie z pomiarami temperatury w punkcie B mierzono zasolenie. Zasolenie ma rozkład normalny. Współczynnik korelacji temperatury i zasolenia wyniósł -0.65.

Jaki test statystyczny pozwoli odpowiedzieć czy na poziomie istotności 5% można przyjąć hipotezę, że oba akweny różnią się w sposób istotny pod względem temperatury wody?

Rozkłady cechy nie są normalne - używamy test nieparametryczny

Mamy 2 akweny - 2 próby niezależne

Wartości powtarzają się często - test Kołmogorowa-Smirnowa

5) Dokonując badan porównawczych nad Zalewem Wiślanym i Zatoka Pucka odłowiono w obu zbiornikach losowo po 25 dorosłych osobników pewnego organizmu i zmierzono ich rozmiar w centymetrach. Odchylenia standardowe pomiarów wyniosły odpowiednio sZW=2,0; sZP=2,1.

a) Jaki należy wybrać test (podaj nazwę i wzór na statystykę testowa), aby odpowiedzieć na pytanie czy te dwa zbiorniki różnią się w sposób istotny pod względem przeciętnych rozmiarów badanego organizmu wiedząc, że próby pochodzą z populacji o rozkładzie normalnym? Jakie należy postawić hipotezy i jaka byłaby odpowiedz na postawione pytanie na poziomie istotności 5%, gdyby wartość statystyki testowej wyniosła 2,0, a P(t>2,0)= 2,85%?

Rozkłady cechy są normalne - test parametryczny

Mamy podane odchylenia - test dotyczący odchylenia

Dwa akweny - 2 próby niezależne

Wybieramy test F-Snedecora, wzór F=(s₁)²/(s₂)²

Hipotezy Ho: sZW=sZP (nie różnią się)

Ha: sZW≠sZP (różnią się)

P(t>2,0)= 2,85%= α/2, więc α=5,7%

α> αgr, przyjmujemy Ho i odpowiadamy, że te dwa zbiorniki nie różnią się

b) Jaki należy wybrać test (podaj nazwę i wzór na statystykę testowa) aby odpowiedzieć na pytanie czy Zatoka Pucka charakteryzuje się większym zróżnicowaniem rozmiarów badanego organizmu wiedząc, że próby pochodzą z populacji o rozkładzie normalnym? Jak powinny brzmieć hipotezy?

Test F-Snedecora F=(s₁)²/(s₂)² ,

Hipotezy Ho: sZW=sZP (nie różnią się)

Ha: sZP>sZW (różnią się)- hipoteza jednostronna

Wówczas P(t>2,0)= 2,85%= α

α < αgr, przyjmujemy Ha, Zatoka Pucka charakteryzuje się większym zróżnicowaniem rozmiarów badanego organizmu niż Zalew Wiślany.

6) Aby ustalić wpływ oczyszczalni ścieków na jakość wody w badanym akwenie postanowiono zbadać koncentracje bakterii w 30 losowo wybranych miejscach akwenu. Badania przeprowadzono w tych samych miejscach dwukrotnie: przed uruchomieniem oczyszczalni i miesiąc po jej uruchomieniu.

a) jaki test pozwoli zweryfikować hipotezę, że oczyszczalnia ścieków nie wpłynęła istotnie na koncentracje bakterii w badanym akwenie, jeżeli rozkład koncentracji bakterii w obu przypadkach można opisać rozkładem normalnym?

Rozkłady normalne-test parametryczny

Jeden akwen- 2 próby zależne (przed i po uruchomieniu oczyszczalni)

Dotyczące średniej - przeciętna ilość bakterii, nie zróżnicowanie wynikow

Test t-Studenta

b) jaki test pozwoli zweryfikować hipotezę, że oczyszczalnia ścieków nie wpłynęła istotnie na koncentracje bakterii w badanym akwenie, jeżeli rozkładu koncentracji bakterii nie można opisać rozkładem normalnym?

Rozkłady nie są normalne- test nieparametryczny, 2 próby zależne

Test Wilcoxona

7) Do tej pory uważano, że przeciętne zasolenie w pewnym akwenie wynosi 7psu. Jaki należy wykorzystać test aby na podstawie pomiaru zasolenia w próbie zweryfikować hipotezę, że nic się pod tym względem nie zmieniło (próba jest losowa i pochodzi z populacji generalnej o rozkładzie normalnym). Jakie hipotezy należy postawić w tym teście?

Rozkłady normalne- test parametryczny

Dotyczące średniej- podane przeciętne zasolenie

Jeden akwen - 1 próba

Test t-Studenta

Hipotezy Ho: x=μ (nie zaszły zmiany)

Ha: x≠ μ (zaszły zmiany)

8) Do tej pory uważano, że odchylenie standardowe zasolenia w pewnym akwenie wynosi 1psu. Jaki należy wykorzystać test aby na podstawie pomiaru zasolenia przyjąć hipotezę, że zróżnicowanie zasoleń w tym akwenie obecnie jest inne (próba jest losowa i pochodzi z populacji generalnej o rozkładzie normalnym)? Jakie hipotezy należy postawić w tym teście?

Rozkłady normalne- test parametryczny

Jeden akwen-1 próba

Podane odchylenie- test dotyczący odchylenia

Test Chi^2

Hipotezy Ho: s=σ (nie zaszły zmiany)

Ha: s≠ σ (zaszły zmiany)

9) Dwóch badaczy niezależnie od siebie przeprowadziło pomiary temperatury w wodach pewnego akwenu. Ich próby były losowe i niezależne i liczyły tyle samo pomiarów. Do tej pory uważano, że rozkład temperatury w tych wodach jest rozkładem normalnym o średniej μ0=10°C. Obaj odrzucili hipotezę, że nadal średnia temperatura wynosi 10°C twierdząc, że średnia temperatura wód w badanym akwenie się zmieniła. Który z nich ma większa szanse popełnienia błędu, jeżeli pierwszy z nich uzyskał statystykę testowa równa -2,5, a drugi -3,0 ? Jakiego rodzaju byłby to błąd?

Na początku należy ustalić jaki test użyli badacze. Był to test t-Studenta (2 próby niezależne, rozkłady normalne, podane średnie).

Badacze odrzucili hipotezę prawdziwą, więc popełnili błąd I rodzaju o prawdopodobieństwie popełnienia błędu α. Jeżeli średnia wynosi 10, to bliżej niej leży wartość -2,5 i P(x<-2,5) jest większe niż P(x<-3).

P(x<-2,5)= α1

P(x<-3)= α2

Tym samym prawdopodobieństwo popełnienia błędu jest większe α1> α2

Ten badacz, który uzyskał statystykę testową (-2,5) popełnia większy błąd.

10) Dokonując badan porównawczych nad Zalewem Wiślanym i Zatoką Pucką odłowiono w obu zbiornikach losowo po 10 dorosłych osobników pewnego gatunku ryb i zmierzono ich rozmiar w centymetrach. Otrzymano wyniki:

Pucka: 25 26 27 28 29 24 23 20 20 21

Wiślany: 29 32 33 34 35 30 31 28 36 37

Jakiego testu należy użyć, aby odpowiedzieć na pytanie, czy te dwa zbiorniki różnią się istotnie pod względem przeciętnych rozmiarów ryb tego gatunku, jeżeli na podstawie tych danych nie można stwierdzić normalności rozkładu rozmiarów?

Rozkłady nie są normalne-test nieparametryczny

Dwa akweny-2 próby niezależne

Test U Manna Whitneya, ponieważ wartości rzadko się powtarzają (mniej niż 50%)

14

---