Transformata Laplace'a wybranych sygnałów

Ćwiczenie 1:

a)

has Laplace transform

b)

has Laplace transform

c)

has Laplace transform

d)

has Laplace transform

e)

has Laplace transform

Ćwiczenie 2:

- Wyznaczyć położenie zer i biegunów na płaszczyźnie zespolonej dla sygnału zdefiniowanego w powyższym przykładzie, gdy parametry  i  wynoszą:

a) =0.5 =25 b) =2 =25 c)  =25 d) =2 =1 e) =2 =10 f) =2 =20 g) =2 =1i h) =2 =0

Jak zmienia się kształt sygnału oraz położenie biegunów i zer jego transmitancji

gdy parametr  rośnie przy stałym  ?

Jak zmienia się kształt sygnału oraz położenie biegunów i zer jego transmitancji

gdy parametr  rośnie przy stałym  ?

a)

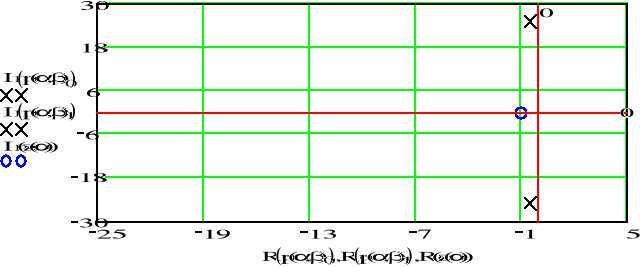
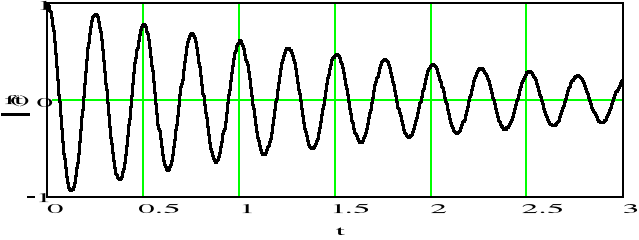
Otrzymaliśmy ten sam sygnał sinusoidalny tłumiony, który jest zadany na początku przykładu

b)

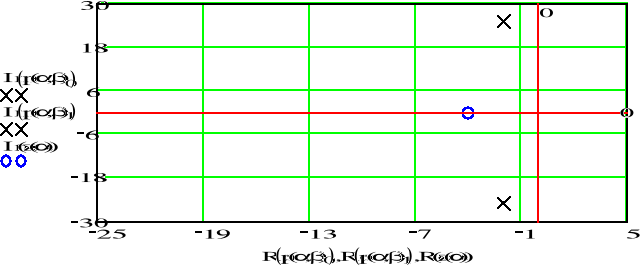
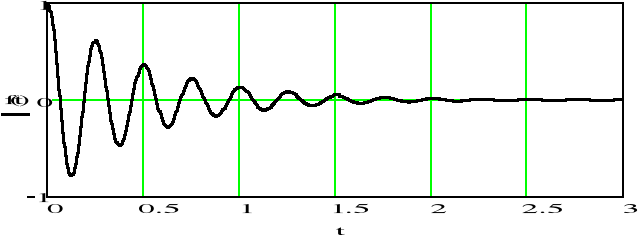
Otrzymaliśmy ten sam sygnał sinusoidalny tłumiony, który jest zadany na poczatku przykładu

c)

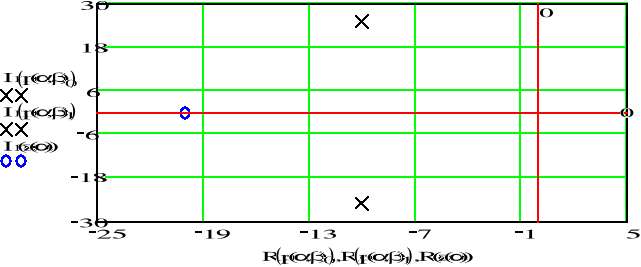
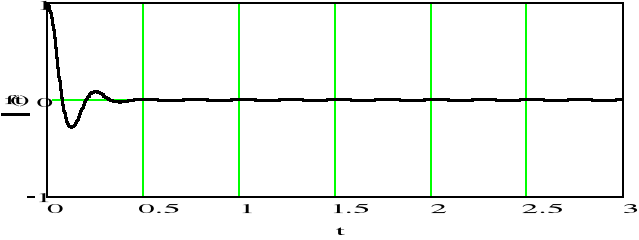
Otrzymaliśmy ten sam sygnał sinusoidalny tłumiony, który jest zadany na poczatku przykładu

d)

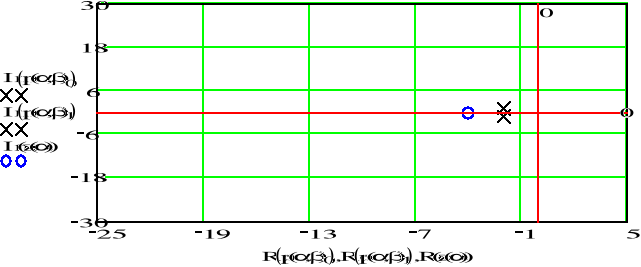
Otrzymaliśmy ten sam sygnał sinusoidalny tłumiony, który jest zadany na poczatku przykładu

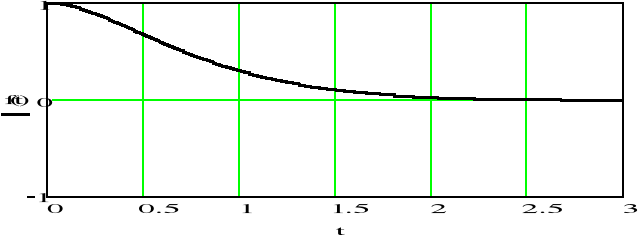
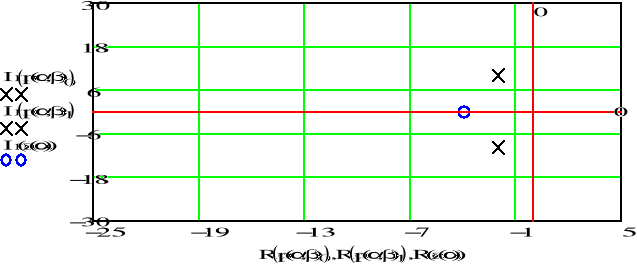
e)

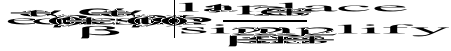
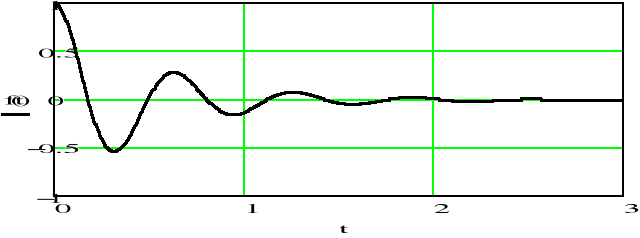
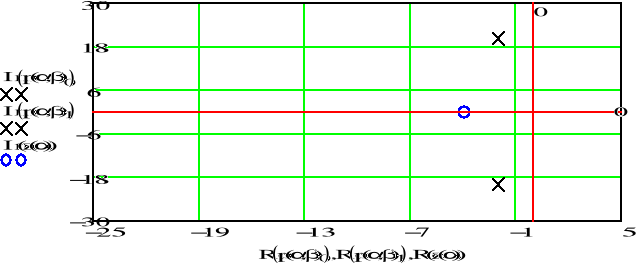
f)

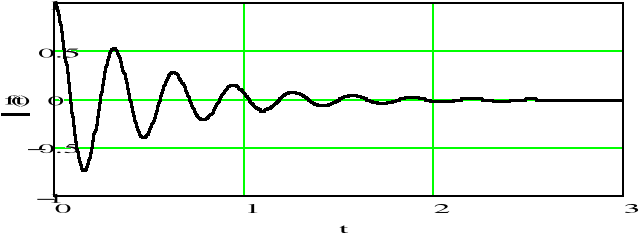
g)

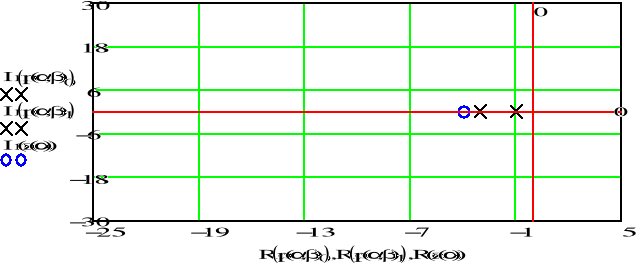
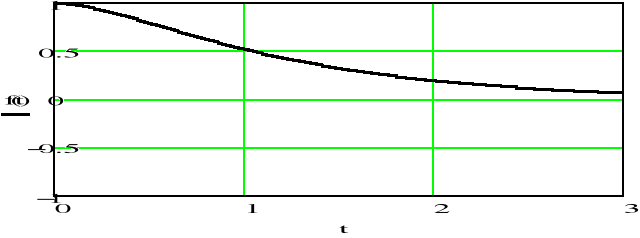
h)

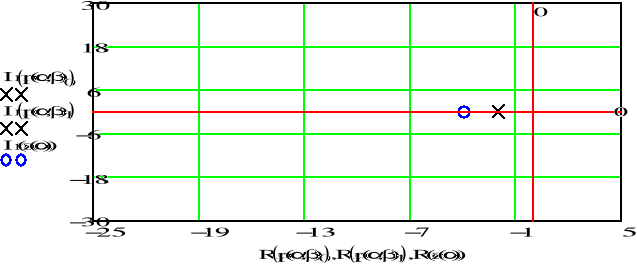
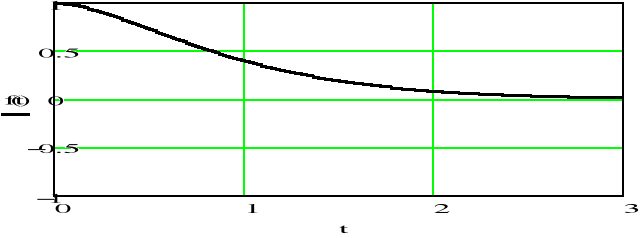
Wnioski:

Gdy parametr  rośnie i parametr  jest stały, częstotliwość sygnału zmniejsza się, co powoduje szybsze jego stłumienie. Bieguny i zera transmitancji sygnału przesuwają się w lewo i przyjmują coraz mniejsze wartości.

Gdy parametr  rośnie i parametr  jest stały, częstotliwość sygnału zwiększa się, bieguny jego transmitancji oddalają się od siebie, a położenie zer nie ulega zmianie.

Ćwiczenie 3:

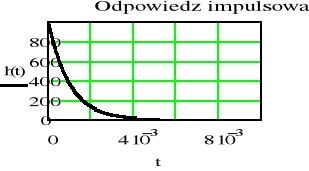
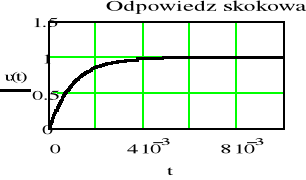
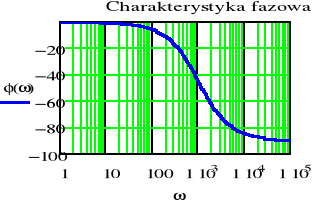
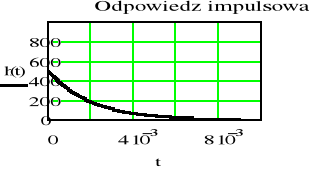
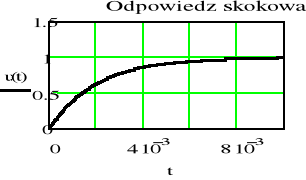
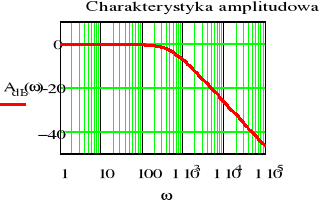
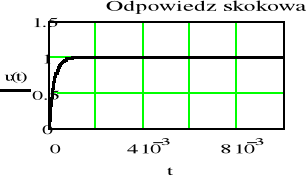
Sporządzić wykresy odpowiedzi impulsowej h(t) i skokowej u(t) filtru dolnoprzepustowego RC dla następujących wartości elementów

a) R=1, C=1 mF b) R=2, C=1 mF c) R=2, C=0.1 mF 1m=10-3

- Porównać częstotliwości graniczne, stałe czasowe oraz czasy w których wyznaczone odpowiedzi osiągają praktycznie stan ustalony dla filtrów od a) do c)

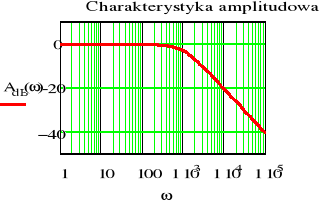
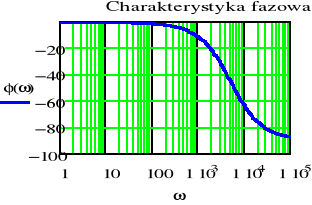
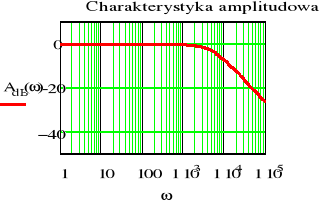
- Wykreślić charakterystykę amplitudową i fazową odpowiedzi skokowej filtru RC o parametrach z punktów od a) do c)

- Wyznaczyć sygnał na wyjściu filtru RC (R=10, C=10mF) dla następujących sygnałów wejściowych:

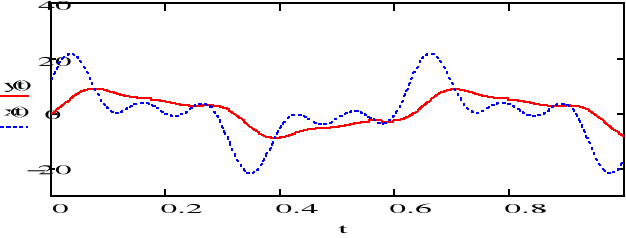
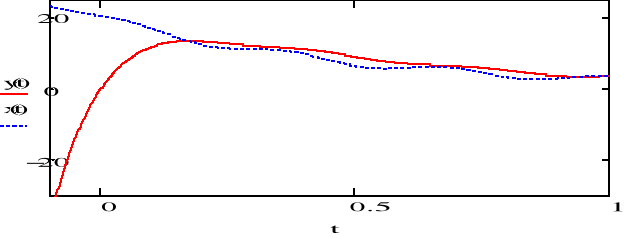
d) 10sin(10t+/3)+7sin(30t+/6)+5sin(50t) e) 20exp(-2t)sin(20t+/6) f) 20exp(-2t)sin(100t+/2)

Wskazówka: odpowiedź na wymuszenie Y(s)=H(s)X(s) jak przy odpowiedzi skokowej lub impulsowej gdzie X(s)=1/s dla skoku jednostkowego lub X(s)=1 dla impulsu Dirac'a.

Wykreślić na jednym wykresie sygnał wejściowy i sygnał wyjściowy.

Wnioski z analizy porównanwczej zamieścić w sprawozdaniu.

a)

b)

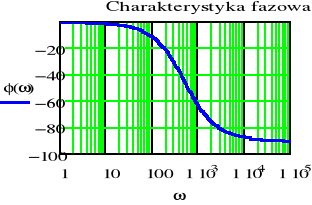
c)

d)

e)

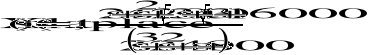
Wnioski:

Sygnał na wyściu filtru RC (R=10, C=10mF) dla odpowiednich sygnałów wejściowych zmniejsza częstotliwość i dąży do 0 wraz z upływem czasu.

---