1. Definicja pochodnej funkcji i interpretacja geometryczna.
● Pochodną funkcji f w punkcie wewnętrznym ![]()
nazywamy liczbę, którą oznaczamy i określamy następująco: ![]()
, przy założeniu, ze powyższa granica istnieje i jest skończona.
Natomiast liczby oznaczone i określane następująco: ![]()
i ![]()
, nazywamy odpowiednio pochodną prawostronną i pochodną lewostronną funkcji f w punkcie ![]()
.
Funkcja ma pochodną w punkcie gdy ma równe obydwie pochodne jednostronne w tym punkcie.
● Interpretacja geometryczna pochodnej:
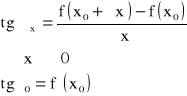
Pochodna ![]()
w punkcie ![]()
jest równa tangensowi kąta nachylenia stycznej do wykresu funkcji ![]()
w punkcie ![]()
względem osi X.
Równanie prostej stycznej (k) do wykresu funkcji f w punkcie ![]()
ma postać: ![]()
.
2. Definicja różniczki funkcji i interpretacja geometryczna. Twierdzenie o przyroście i jego zastosowania.
● Niech funkcja f ma w punkcie wewnętrznym ![]()
pochodną ![]()
. Różniczką funkcji f w punkcie ![]()
nazywamy funkcją liniową, którą oznaczamy i określamy wzorem: ![]()
, ![]()
.
Różniczkę funkcji ![]()
można oznaczać krótko przez df.
● Interpretacja geometryczna różniczki:
● Twierdzenie (o przedstawianiu przyrostu funkcji):
Jeśli funkcja f ma w punkcie wewnętrznym ![]()
pochodną ![]()
, to jej przyrost można przedstawić w postaci ![]()
dla ![]()
, przy czym ![]()
.
● Zastosowanie różniczki:
Gdy funkcja f ma w punkcie wewn. ![]()
pochodną ![]()
i przyrost argumentu dx jest bliski 0, to:
1) przyrost funkcji można przybliżyć różniczką, a więc ![]()
dla ![]()
gdzie ![]()
bliskie 0.
2) wartość funkcji można przybliżyć wzorem ![]()
dla ![]()
gdzie ![]()
bliskie 0.
3. Podać twierdzenie de L'Hospitala.
● Twierdzenie de L'Hospitala:
Jeśli:
1) funkcje f i g mają pochodną w pewnym sąsiedztwie punktu ![]()
,
2) granice ![]()
(lub ![]()
),
3) istnieje granica ![]()
właściwa lub niewłaściwa,
to istnieje granica ![]()
.
Uwaga: Twierdzenie to jest słuszne, gdy punkt ![]()
jest niewłaściwy (![]()
lub ![]()
), oraz jest słuszne dla granic jednostronnych.
4. Podać twierdzenie Lagrangea wraz z interpretacją geometryczną. Wnioski z twierdzenia.
● Twierdzenie Lagrangea:
Jeśli funkcja f jest ciągła w przedziale domkniętym ![]()
i pochodną w przedziale ![]()
to istnieje punkt ![]()
taki, że: ![]()
.
● Interpretacja geometryczna twierdzenia Lagrangea:
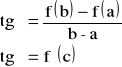
Istnieje na wykresie funkcji taki punkt ![]()
, że styczna do wykresu w tym punkcie jest równoległa do siecznej przechodzącej przez punkty ![]()
i ![]()
.
● Wnioski z twierdzenia Lagrangea:
Jeśli funkcja f ma pochodną w przedziale ![]()
oraz:
1) ![]()
to funkcja f jest rosnąca w przedziale I;
2) ![]()
to funkcja f jest malejąca w przedziale I;
3) ![]()
to funkcja f jest stała w przedziale I.
5. Podać twierdzenie Taylora.
● Twierdzenie (wzór Taylora):
Jeśli funkcja f ma pochodną n-tego rzędu w przedziale ![]()
, to dla ustalonego punktu ![]()
i dowolnego punktu ![]()
istnieje liczba ![]()
taka, że zachodzi wzór:
![]()
, gdzie: ![]()
- reszta Lagrangea.
● Wniosek z twierdzenia Taylora:
Dla wartości x bliskich ![]()
wartość funkcji f(x) można przybliżyć wielomianem n-1 stopnia, a więc:
![]()
, dla ![]()
, δ bliskie 0; przy czym moduł reszty ![]()
określa błąd tego przybliżenia.
6. Definicja ekstremum funkcji (rys.). Warunek konieczny na ekstremum i uwagi.
●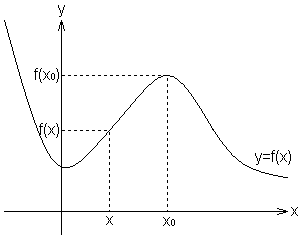
Mówimy, że funkcja f ma w punkcie wewnętrznym ![]()
:
maximum lokalne (właściwe)
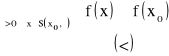
minimum lokalne (właściwe)
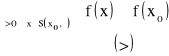
Maxima i minima lokalne nazywamy ekstremami.
● Twierdzenie (warunek konieczny na ekstremum):
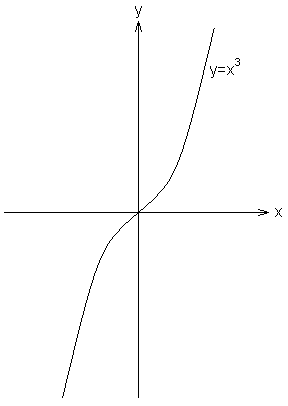
Jeśli funkcja f ma w punkcie wewnętrznym ![]()
ekstremum lokalne i ma w tym punkcie pochodną ![]()
, to ![]()
.
● Uwaga:
Twierdzenie odwrotne nie jest prawdziwe:
np. funkcja ![]()
ma pochodną ![]()
taką, że ![]()
, ale nie ma w punkcie ![]()
ekstremum.
7. Podać pierwszy i drugi warunek dostateczny na ekstremum.
● Twierdzenie (pierwszy warunek dostateczny na istnienie ekstremum):
Jeśli funkcja f jest ciągła w punkcie wewnętrznym ![]()
i ma pochodną w sąsiedztwie ![]()
taką, że spełnione są warunki:
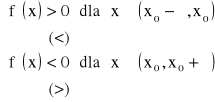
, to funkcja ma w punkcie ![]()
maximum (minimum) lokalne właściwe.
● Twierdzenie (drugi warunek dostateczny na istnienie ekstremum):
Jeśli funkcja f ma n-tą pochodną parzystego rzędu w pewnym otoczeniu punktu wewnętrznego ![]()
ciągłą w tym punkcie oraz ![]()
i 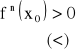
to funkcja ma w punkcie ![]()
minimum (maximum) lokalne właściwe. Dowód wynika ze wzoru Taylora.
8. Definicja funkcji pierwotnej. Twierdzenie podstawowe o funkcjach pierwotnych z dowodem. Definicja całki nieoznaczonej.
● Funkcją pierwotną funkcji f w przedziale ![]()
nazywamy funkcję F określoną w tym przedziale, taką, że: ![]()
dla ![]()
.
Poszukiwanie funkcji pierwotnej danej funkcji jest operacją odwrotną do wyznaczania pochodnej.
● Twierdzenie (podstawowe o funkcjach pierwotnych):
Każde dwie funkcje pierwotne F i G funkcji f w przedziale I różnią się o funkcję stałą, co oznacza, że ![]()
dla ![]()
.
Dowód: Niech funkcje F i G będą pierwotne funkcji f w przedziale I. Rozpatrzmy funkcję ![]()
dla ![]()
. Ponieważ ![]()
dla ![]()
to z wniosku trzeciego twierdzenia Lagrangea wynika, że: ![]()
dla ![]()
![]()
dla ![]()
. [„Co należało udowodnić!”]
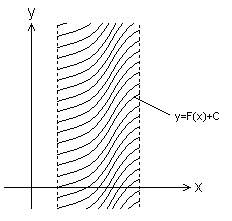
● Całką nieoznaczoną funkcji f w przedziale I nazywamy zbiór wszystkich funkcji pierwotnych funkcji f w przedziale I, który oznaczamy: ![]()
, gdzie F jest funkcją pierwotną funkcji f w przedziale I, a C jest dowolną stałą.
● Wyznaczanie funkcji pierwotnej danej funkcji nazywamy całkowaniem tej funkcji.
O funkcji, która ma w przedziale funkcję pierwotną mówimy, że jest całkowalna w tym przedziale.
9. Podać twierdzenia o całkowaniu przez części i podstawianiu.
● Twierdzenie (o całkowaniu przez części)
Jeśli funkcje u i v mają ciągłe pochodne w przedziale I, to zachodzi wzór ![]()
dla ![]()
.
● Twierdzenie (o całkowaniu przez podstawianie ![]()
)
Jeśli funkcja h ma ciągłą pochodną w przedziale I a funkcja g jest ciągła w przedziale h(I) to zachodzi wzór: 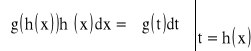
dla ![]()
.
10. Wstęp do definicji i definicja całki oznaczonej właściwej z uwagami.
● Niech funkcja f będzie określona i ograniczona w przedziale domkniętym ![]()
. Przedział domknięty ![]()
dzielimy na n przedziałów dowolnie wybranymi punktami ![]()
, przy czym ![]()
. ● Opisany podział przedziału ![]()
na n przedziałów ![]()
dla ![]()
oznaczamy symbolem ![]()
, a więc ![]()
. ● Długość przedziału ![]()
oznaczamy przez ![]()
, a więc ![]()
dla ![]()
. ● Największą z liczb ![]()
dla ![]()
nazywamy średnią przedziału ![]()
i oznaczamy przez ![]()
, a więc: ![]()
. ● W każdym przedziale ![]()
wybieramy po jednym punkcie ![]()
dla ![]()
. ● Tworzymy sumę całkową podziału ![]()
, a więc ![]()
. ● Weźmy następnie ciąg podziałów ![]()
przedziału ![]()
taki, że ![]()
, który nazywamy ciągiem podziałów normalnych.
● Jeśli dla każdego ciągu podziałów normalnych ![]()
przedziału ![]()
i dowolnym wyborze punktów ![]()
ciąg sum całkowych ![]()
jest zbieżny do tej samej granicy właściwej, to granicę tę nazywamy całką oznaczoną Reimanna funkcji f po przedziale ![]()
i oznaczamy: 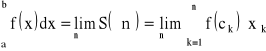
. Przedział ![]()
nazywamy przedziałem całkowania funkcji f, liczbę a (b) nazywamy dolną (górną) granicą całkowania, a f nazywamy funkcją podcałkową.
● Uwagi:
1) Jeśli funkcja f jest całkowalna w przedziale domkniętym to jest ograniczona w tym przedziale, ale nie odwrotnie. Stąd wynika, że funkcja nieograniczona w przedziale nie jest w tym przedziale całkowalna, a funkcja ograniczona w przedziale może być w tym przedziale całkowalna;
2) Istnieją funkcje ograniczone w przedziale domkniętym, które nie są w tym przedziale całkowalne, np. funkcja Dirichletta, która jest ograniczona w przedziale domkniętym ![]()
, ale nie jest w nim całkowalna.
3) Każda funkcja ciągła w przedziale domkniętym jest w tym przedziale całkowalna;
4) Istnieją funkcje ograniczone i nieciągłe w przedziale domkniętym, które są całkowalne w tym przedziale. Funkcjami takimi są funkcje ograniczone, posiadające tylko skończoną liczbę punktów nieciągłości w tym przedziale;
5) 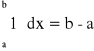
;
6) Symbol całki oznaczonej można rozszerzyć:
a) 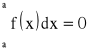
b)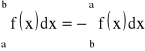
gdy ![]()
.
11. Własności całki oznaczonej. Podać twierdzenia o wartości średniej i główne.
● Własności całki oznaczonej:
1) Jeśli funkcja f jest całkowalna na przedziale ![]()
i ![]()
to funkcja ![]()
jest też całkowalna na tym przedziale i zachodzi wzór: 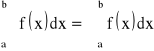
;
2) Jeśli funkcje f i g są całkowalne na przedziale ![]()
, to funkcja f+g też jest całkowalna na tym przedziale i zachodzi wzór: 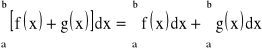
;
3) Jeśli funkcja f jest całkowalna na przedziale ![]()
i ![]()
to jest całkowalna w przedziale ![]()
i ![]()
oraz zachodzi wzór: 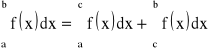
;
4) Jeśli funkcje f i g są całkowalne na przedziale ![]()
oraz ![]()
dla ![]()
to zachodzą nierówności: 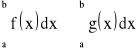
;
5) Jeśli funkcja f jest całkowalna na przedziale ![]()
, to funkcja ![]()
jest też całkowalna na tym przedziale i zachodzi nierówność: 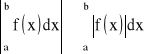
;
6) Jeśli funkcja f jest całkowalna na przedziale ![]()
, to zachodzi nierówność ![]()
![]()
i ![]()
![]()
.
● Twierdzenie (o wartości średniej dla całki oznaczonej):
Jeśli funkcja f jest ciągła w przedziale ![]()
to jest całkowalna w tym przedziale i istnieje punkt ![]()
taki, że zachodzi równość: 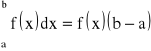
.
● Twierdzenie (pierwsze twierdzenie główne rachunku całkowego):
Jeśli funkcja f jest ciągła w przedziale ![]()
, to funkcja 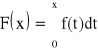
dla ![]()
ma pochodną w przedziale ![]()
oraz ![]()
dla ![]()
.
● Twierdzenie (drugie twierdzenie główne rachunku całkowego):
Jeśli funkcja f jest ciągła w przedziale ![]()
a funkcja F jest funkcją pierwotną funkcji f w przedziale ![]()
to zachodzi wzór: 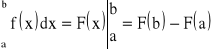
.
12. Definicja całki niewłaściwej pierwszego rodzaju.
Niech funkcja f będzie określona w przedziale nieograniczonym ![]()
i będzie ograniczona oraz całkowalna w każdym przedziale ![]()
dla ![]()
. Całką niewłaściwą pierwszego rodzaju funkcji f po przedziale ![]()
nazywamy granicę właściwą, którą oznaczamy: 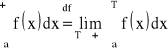
.
Gdy powyższa granica jest niewłaściwa lub nie istnieje, to mówimy, że całka niewłaściwa pierwszego rodzaju jest rozbieżna, a w pewnym przypadku mówimy, że jest zbieżna.
13. Definicja całki niewłaściwej drugiego rodzaju.
Niech funkcja f będzie określona w przedziale ograniczonym ![]()
i będzie nieograniczona w lewostronnym sąsiedztwie punktu b oraz całkowalna w każdym przedziale ![]()
dla ![]()
. Całką niewłaściwą drugiego rodzaju funkcji f po przedziale ![]()
nazywamy granicę właściwą, którą oznaczamy: 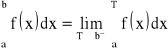
.
Gdy powyższa granica jest niewłaściwa lub nie istnieje, to mówimy, że całka niewłaściwa drugiego rodzaju jest rozbieżna, a w pewnym przypadku mówimy, że jest zbieżna.
14. Zastosowania geometryczne całek z interpretacją geometryczną.
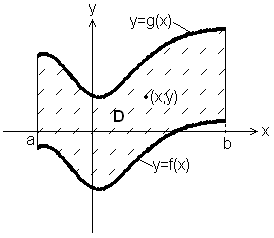
● Pole obszaru płaskiego:
Niech funkcje f i g będą ciągłe w przedziale domkniętym ![]()
oraz ![]()
dla ![]()
.
Wtedy pole obszaru D wyraża się wzorem: 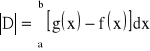
.
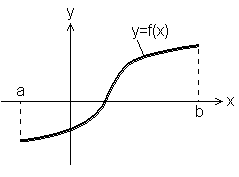
● Długość łuku krzywej płaskiej:
Niech funkcja f będzie klasy C1 w przedziale ![]()
.
Wtedy długość łuku krzywej L: ![]()
dla ![]()
jest określona wzorem: 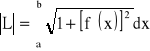
.
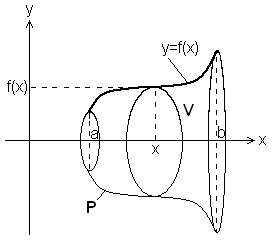
● Objętość i pole powierzchni bocznej obszaru obrotowego.
- Niech funkcja f będzie ciągła w przedziale ![]()
.
Objętość obszaru płaskiego powstałego przez obrót krzywej L: ![]()
dla ![]()
dookoła osi X wyraża się wzorem: 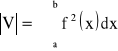
.
- Niech funkcja będzie klasy C1 w przedziale ![]()
. Pole powierzchni bocznej obszaru powstałego przez obrót krzywej L: ![]()
dla ![]()
wokół osi X wyraża się wzorem: 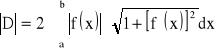
.
15. Definicja szeregu i zbieżności.
● Szeregiem liczbowym nieskończonym utworzonym z ciągu liczbowego ![]()
nazywamy formalną sumę wyrazów tego ciągu którą oznaczamy: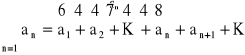
Liczbę ![]()
nazywamy n-tym wyrazem tego szeregu a liczbę ![]()
nazywamy n-tą sumą częściową szeregu.
● Mówimy, że szereg liczbowy ![]()
jest zbieżny wtedy, gdy ciąg sum częściowych (Sn) tego szeregu jest zbieżny do granicy skończonej (właściwej), co oznacza że ![]()
.
Liczbę S nazywamy sumą tego szeregu i zapisujemy że: ![]()
. Szereg który nie jest zbieżny nazywamy rozbieżnym. Szereg zbieżny ma sumę, a rozbieżny nie ma sumy.
16. Kryterium całkowe i porównawcze zbieżności szeregu.
● Twierdzenie (kryterium całkowe):
Jeśli funkcja f jest nieujemna i ciągła w przedziale ![]()
, to szereg 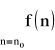
jest zbieżny (rozbieżny) gdy całka niewłaściwa 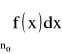
jest zbieżna (rozbieżna).
Interpretacja geometryczna kryterium w przypadku gdy całka niewłaściwa jest zbieżna:
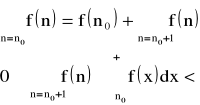
● Twierdzenie (kryterium porównawcze):
Jeśli ![]()
oraz:
a) szereg ![]()
jest zbieżny, to szereg ![]()
też jest zbieżny;
b) szereg ![]()
jest rozbieżny, to szereg ![]()
też jest rozbieżny.
17. Definicja zbieżności bezwzględnej i warunkowej szeregu. Kryteria d'Alamberta i Cauchyego.
● Mówimy, że szereg zbieżny ![]()
jest:
a) zbieżny bezwzględnie, gdy szereg modułów ![]()
jest zbieżny;
b) zbieżny warunkowo, gdy szereg modułów ![]()
jest rozbieżny.
● Twierdzenie (o zbieżności bezwzględnej):
Jeżeli szereg ![]()
jest zbieżny, to szereg ![]()
jest zbieżny (bezwzględnie).
● Twierdzenie (kryterium d'Alamberta):
Jeśli istnieje granica skończona lub nieskończona 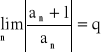
oraz:
1) ![]()
to szereg ![]()
jest zbieżny bezwzględnie;
2) ![]()
to szereg ![]()
jest rozbieżny;
3) ![]()
to nic nie wiadomo.
● Twierdzenie (kryterium Cauchyego):
Jeśli istnieje granica skończona lub nieskończona ![]()
oraz:
1) ![]()
to szereg ![]()
jest zbieżny bezwzględnie;
2) ![]()
to szereg ![]()
jest rozbieżny;
3) ![]()
to nic nie wiadomo.
18. Szeregi przemienne. Kryterium Leibnitza.
● Niech ![]()
dla ![]()
. Szereg liczbowy postaci: ![]()
nazywamy szeregiem przemiennym.
● Twierdzenie (kryterium Leibnitza):
Jeśli:
1) ![]()
;
2) ![]()
[ciąg (bn) jest nierosnący];
3) ![]()
;
to szereg przemienny ![]()
jest zbieżny.
19. Definicja szeregu potęgowego i promienia zbieżności.
● Szeregiem potęgowym o środku w punkcie ![]()
nazywamy szereg funkcyjny postaci: ![]()
. Ustalone liczby rzeczywiste ![]()
nazywamy współczynnikami szeregu potęgowego. Łatwo zauważyć, że szereg potęgowy jest zawsze zbieżny w punkcie ![]()
(wtedy ![]()
.
● Promieniem zbieżności szeregu potęgowego ![]()
nazywamy liczbę ![]()
taką, że szereg jest zbieżny w przedziale ![]()
, z rozbieżny w zbiorze ![]()
.
Gdy szereg potęgowy jest zbieżny tylko w punkcie ![]()
to przyjmujemy, że R=0.
Gdy szereg potęgowy jest zbieżny w każdym punkcie ![]()
, to przyjmujemy, że R=∞.
20. Twierdzenie o rozwijaniu funkcji w szereg Taylora. Podstawowe rozwinięcia.
● Twierdzenie (o rozwijaniu funkcji w szereg potęgowy):
Niech funkcja f będzie klasy ![]()
w przedziale ![]()
. Wtedy dla ustalonego punktu ![]()
i dowolnego punktu ![]()
istnieje liczba ![]()
taka, że zachodzi wzór Taylora: ![]()
, gdzie: ![]()
dla ![]()
.
● Jeśli dla ustalonego ![]()
granica ![]()
to funkcję można przedstawić w postaci sumy szeregu potęgowego Taylora o środku w punkcie ![]()
, a więc: ![]()
dla ![]()
, lub krótko: 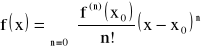
dla ![]()
.
Gdy ![]()
to szereg Taylora nazywamy szeregiem Maclaurina.
Strona 9 z 10
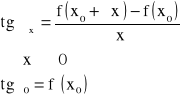
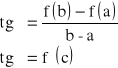
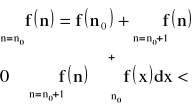
- ta suma jest równa polu obszaru zakresko-wanego
Wyszukiwarka
Podobne podstrony:
mat, fiz, pnom, Matematyka - odpowiedzi na repetytorium I, Omów siły i energie oddziaływań między at
Zebrane odpowiedzi na pytania, Inżynieria materiałowa pwr, Ochrona własności intelektualnej
Maszynoznastwo odpowiedzi na pytania, studia materiały, Masyznoynastwo
ODPOWIEDZI NA PYTANIA, Logistyka - materiały, semestr 1, Podstawy zarządzania
ZESTAW PYTAŃ I ODPOWIEDZI NA LICENCJĘ II st ustny 70pyt 17str
Matematyka 1semestr, Politechnika Lubelska, Studia, sem I - II, materialy na studia
Odpowiedzi na pytania z kartki, Prywatne, Uczelnia, Budownictwo, II Semestr, Materiały Budowlane, ma
Miniewicz, materiały zaawansowane technologicznie, odpowiedzi na zagadnienia
lista poleceń, Politechnika Lubelska, Studia, Studia, sem I - II, materialy na studia
Zestaw pytań i odpowiedzi na II stopień, TESTY OCHRONY, testy
25 siła grupy II, Materiały na zajęcia teatralne, Praca WARSZTATY TEATRALNE
sprawozdnie 5, Politechnika Lubelska, Studia, Studia, sem I - II, materialy na studia
Semestr II - Materiały od RM, UJK.Fizjoterapia, - Notatki - Rok I -, Biofizyka, Materiały na zalicze
MateriałoznawstwoII, odpowiedzi na zagadnienia, Wykład 7
odpowiedzi na pytania z poprzednich lat, Ogrodnictwo, Semestr II, Genetyka, Genetyka egzaminnn
odpowiedzi na polimery - polowa, AGH IMIR AiR, S2, PNOM - Podstawy nauki o materiałach
ua2 - kolejne odpowiedzi na pytania, wat elektronika, analogi, Układy analogowe, analogi, analogizal
więcej podobnych podstron