MATEMATYKA - ODPOWIEDZI NA REPETYTORIUM

1. Definicja modułu i argumentu liczny zespolonej. Postać trygonometryczna i wzór Moivrea. Obliczyć np.
   .

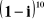
Modułem liczby zespolonej
nazywamy liczbę rzeczywistą
. Ponieważ
to stąd mamy
.

Argumentem liczby zespolonej
nazywamy każdą liczbę rzeczywistą
spełniającą układ równań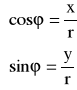
.

Postać trygonometryczna: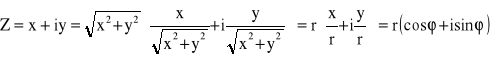
.

Twierdzenie (wzór Moivrea):

Dla dowolnej liczby zespolonej danej w postaci trygonometrycznej
i dowolnej liczny naturalnej
zachodzi wzór:
.

2. Definicja pierwiastka liczby zespolonej. Twierdzenie o pierwiastkowaniu liczby zespolonej. Znaleźć pierwiastki np.
   .

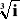
Pierwiastkiem n-tego stopnia liczby zespolonej
nazywamy każdą liczbę zespoloną W taką, że
.

Zbiór wszystkich pierwiastków n-tego stopnia liczby zespolonej Z oznaczamy przez
.

Twierdzenie (o pierwiastkach liczby zespolonej)
Każda liczba zespolona Z różna od 0 ma dokładnie n różnych pierwiastków n-tego stopnia w zbiorze liczb zespolonych C.

Gdy liczbę zespoloną Z przedstawiamy w postaci trygonometrycznej
, to tymi pierwiastkami są liczby zespolone postaci
dla
.

3. Twierdzenie podstawowe algebry i własność wielomianu zespolonego i współczynnikach rzeczywistych. Znaleźć rozkład wielomianu na czynniki (przykład).

Twierdzenie (podstawowe twierdzenie algebry)

Każdy wielomian zespolony
, dla
, stopnia
, ma w zbiorze liczb zespolonych dokładnie n miejsc zerowych.

Twierdzenie (własność wielomianu o współczynnikach rzeczywistych)

Jeśli wielomian n-tego stopnia
, dla
ma współczynniki rzeczywiste
oraz liczna zespolona
jest miejscem zerowym tego wielomianu
, to również liczba
jest miejscem zerowym tego wielomianu

4. Definicja wyznacznika macierzy. Własności wyznaczników. Obliczyć wyznacznik macierzy…

Wyznacznikiem macierzy kwadratowej n-tego stopnia
nazywamy liczbę
, określoną rekurencyjnie (rozwinięcie wyznacznika dla pierwszego wiersza).

Dla
,

Dla
,
,

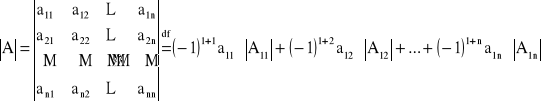
gdzie
jest podmacierzą macierzy A, powstałą przez skreślenie w niej i-tego wiersza i j-tej kolumny.

Własności wyznaczników:
1) Wyznacznik macierzy zawierającej wiersze (kolumny) złożone z samych 0, jest równy 0;

2) Wyznacznik macierzy zawierającej dwa wiersze (kolumny) proporcjonalne jest równy 0;

3) Wyznacznik macierzy trójkątnej jest równy iloczynowi elementów głównej przekątnej;

4) Zmiana dwóch wierszy (kolumn) macierzy zmienia znak wyznacznika;

5) Wspólny czynnik z wiersza (kolumny) macierzy można wynieść przed wyznacznik;

6) Wyznacznik macierzy nie ulegnie zmiany, gdy do pewnego wiersza (kolumny) macierzy dodamy inny wiersz (kolumnę) pomnożony przez liczbę.

5. Definicja macierzy odwrotnej. Metoda wyznaczania macierzy odwrotnej. Znaleźć macierz odwrotną macierzy…

Macierzą odwrotną macierzy kwadratowej A nazywamy macierz kwadratową
taką, że
(macierz jednostkowa). Gdy macierz A jest nieosobliwa, co oznacza, że wyznacznik
, to jest odwracalna. Gdy macierz A jest osobliwa, co oznacza, że wyznacznik
, to nie jest odwracalna.

Procedura odwracania macierzy:

1) Obliczany wyznacznik macierzy i niech
;

2) Wyznaczamy macierz dopełnień macierzy A, taką, że
;

3) Wyznaczamy macierz dołączoną macierzy A ze wzoru
;

4) Macierz odwrotną macierzy A wyznaczamy ze wzoru
.

6. Definicja rządu macierzy. Własności rządu macierzy. Korzystając z własności obliczyć rząd macierzy…

Rządem macierzy prostokątnej
nazywamy największy stopień podmacierzy kwadratowej macierzy o wyznaczniku różnym od 0. Rząd macierzy A będziemy oznaczać przez
. Liczba ta spełnia nierówność
.

Własności rządu macierzy:
Rząd macierzy nie ulegnie zmiany, gdy…

1) usuniemy z macierzy wiersz (kolumną) złożony z samych 0;

2) usuniemy z macierzy jeden z dwóch wierzy (kolumn) proporcjonalnych;

3) dwa wiersze (kolumny) macierzy zamienimy miejscami;

4) pomnożymy wiersz (kolumnę) macierzy przez liczbę różną od 0;

5) do pierwszego wiersza (kolumny) macierzy dodamy inny wiersz (kolumnę) pomnożony przez liczbę.

Powyższe własności nazywamy przekształceniami elementarnymi dokonywanymi na wierszach (kolumnach) macierzy.

Wykonując przekształcenia elementarne na wierszach (kolumnach) macierzy każdą macierz można sprowadzić do równoważnej macierzy bazowej, która zawiera maksymalną liczbę różnych jednostkowych wektorów kolumnowych. Liczba tych wektorów jest równa rządowi macierzy.

7. Definicja ogólnego układu równań liniowych. Twierdzenie Kroneckera-Capelliego. Zbadać rozwiązalność układu równań liniowych…

Układem m równań liniowych o n niewiadomych nazywamy układ równań postaci:

,

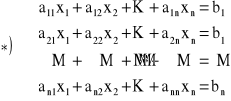
gdzie
i
dla
;
są ustalonymi liczbami rzeczywistymi.

Jeśli
dla
to układ równań nazywamy jednorodnym, a w przeciwnym wypadku niejednorodnym.

Rozwiązaniem szczególnym układu równań liniowych
nazywamy zbiór liczb
spełniające każde równanie układu. Zbiór wszystkich rozwiązań szczególnych nazywamy rozwiązaniem ogólnym.

Twierdzenie (Kroneckera-Capelliego):

Układ m równań liniowych o n niewiadomych…

1) ma dokładnie jedno rozwiązanie (jest on oznaczony) wtedy i tylko wtedy, gdy
i
;

2) ma nieskończenie wiele rozwiązań (jest nieoznaczony) wtedy i tylko wtedy, gdy
i
;

3) nie ma rozwiązań (jest sprzeczny) wtedy i tylko wtedy, gdy
.

8. Definicja działań na wektorach. Definicja i własności iloczynu skalarnego wektorów. Długość wektora i jego własności.

Zbiór
wektorów swobodnych, w którym są określone działania dodawania i mnożenia wektorów przez liczny rzeczywiste następująco:

, jest n-wymiarową przestrzenią wektorową, którą nazywamy n-wymiarową przestrzenią kartezjańską wektorową.

Iloczynem skalarnym wektorów
i
nazywamy liczbę:
.

Własności iloczynu skalarnego:

1)
;

2)
;

3)
;

4)
.

Łatwo zauważyć, że
, a stąd wynika, że długość wektora
wyraża się wzorem
.

Własności długości wektora:

1)
;

2)
;

3)
;

4)
;

5)
;

9. Definicje wektorów równoległych, prostopadłych, kąta między wektorami i pola trójkąta. Obliczyć kąt w trójkącie…

Mówimy, że wektory
i
są równoległe, co zapisujemy
.

Gdy
to mówimy, że wektory mają zgodne zwroty.

Gdy
to mówimy, że wektory mają zwroty przeciwne.

Mówimy, że wektory
i
są prostopadłe (ortogonalne), co zapisujemy
.

Kątem pomiędzy niezerowymi wektorami
i
nazywamy liczbę
taką, że
.

Polem trójkąta rozpiętego na wektorach
i
nazywamy liczbę
.

10. Definicja iloczynu wektorowego wektorów, interpretacja geometryczna. Metoda obliczania i własności. Obliczyć pole trójką o wierzchołkach…

Iloczynem wektorowym wektorów nierównoległych
i
nazywamy wektor
, o własnościach:

1) Kierunek: Wektor
jest prostopadły do wektorów
i
;

2) Długość:
- dwa pola trójkąta;

3) Zwrot: Orientacja
.

Gdy wektory
i
są równoległe to przyjmujemy
.

Interpretacja geometryczna iloczynu wektorowego:

Twierdzenie (o wyznaczniku iloczynu wektorowego wektorów)

Iloczyn wektorowy wektorów
i
jest określony wzorem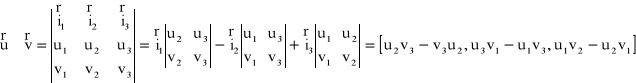
.

Własności iloczynu wektorowego:

1)
;

2)
;

3)
;

11. Definicja płaszczyzny w przestrzeni R³. Postać parametryczna i kanoniczna płaszczyzny. Znaleźć równanie płaszczyzny…

Płaszczyzna w przestrzeni
przechodząca przez ustalony punkt
należący do przestrzeni
oraz równoległa do ustalonych nierównoległych wektorów
i
nazywamy zbiór punktów
taki, że
dla
.

Zapisując punkty i wektory we współrzędnych otrzymamy opis parametryczny płaszczyzny: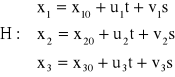
dla
.

Eliminując z opisu parametrycznego płaszczyzny parametry t i s otrzymamy postać kanoniczną płaszczyzny
, gdzie wektor
jest niezerowy i prostopadły do płaszczyzny H, a więc
.

12. Podać wzory na odległość punktu od płaszczyzny danej w postaci parametrycznej lub kanonicznej z objaśnieniami. Znaleźć odległość punkty A=(2, -1, 3) od płaszczyzny H: 3x₁ - 2x₂ + 4x₃ + 4 = 0.

Wzór na odległość punktu
od płaszczyzny określonej parametrycznie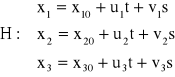

lub kanonicznie
, zawierającej punkt
i równoległej do nierównoległych wektorów
i
oraz prostopadłej do wektora
, jest postaci: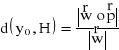
, gdzie:
- wektor o początku w punkcie
i końcu w punkcie
.

By z równania postaci parametrycznej otrzymać wektor
należy pomnożyć wektorowo wektory
i
. Wtedy wzór ten jest postaci: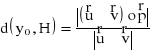
.

13. Definicja prostej w przestrzeni R³. Postać parametryczna, kierunkowa i krawędziowa. Znaleźć prostą w tych postaciach…

Prostą w przestrzeni
, przechodzącą przez ustalony punkt
i równoległą do niezerowego ustalonego wektora
nazywamy zbiór punktów
, taki, że:
, dla
.

Zapisując punkty i wektory we współrzędnych, otrzymamy opis parametryczny prostej: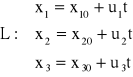
, dla
.

Eliminując z powyższego układu równań parametr t przy założeniach, że
, otrzymamy postać kierunkową:
.

Dwie nierównoległe płaszczyzny wyznaczają prostą. Postać tę nazywamy postacią krawędziową prostej: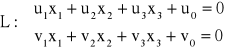
.

14. Podać wzory na odległość prostych równoległych oraz prostych skośnych. Znaleźć odległość między prostymi
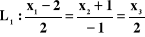
    i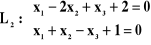
    .

Wzór na odległość prostych równoległych
i
, przechodzących przez punkty
i
oraz równoległych do wektora
jest postaci: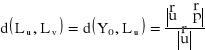
, gdzie
- wektor o początku w punkcie
i końcu w punkcie
.

Wzór na odległość prostych skośnych
i
, przechodzących przez punkty
i
oraz równoległych do wektora
i
jest postaci: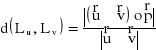
, gdzie
- wektor o początku w punkcie
i końcu w punkcie
.

15. Podać definicję ciągu liczbowego oraz definicje ciągu monotonicznego i ograniczonego. Zbadać monotoniczność i ograniczoność ciągu…

Ciągiem liczbowym nieskończonym nazywamy funkcję przyporządkowującą każdej liczbie naturalnej
dokładnie jedną liczbę rzeczywistą
.

Ciąg
nazywamy:

a) monotonicznie rosnącym
;

b) monotonicznie niemalejącym
;

c) monotonicznie malejącym
;

d) monotonicznie nierosnącym
.

Ciąg
jest:

a) ograniczony z góry
;

b) ograniczony z dołu
;

c) ograniczony
gdy jest ograniczony z góry lub z dołu.

16. Podać definicję granicy ciągu oraz wykazać z definicji, że
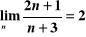
    . Podać własności ciągów zbieżnych.

Granicą ciągu liczbowego
nazywamy liczbę g, co zapisujemy
.

Własności ciągów zbieżnych:

1) Ciąg zbieżny ma tylko jedną granicę;

2) Ciąg zbieżny jest ograniczony;

3) Każdy ciąg częściowy (podciąg), wybrany z ciągu zbieżnego, jest zbieżny do tej samej granicy, co ciąg;

4) Gdy ciąg zawiera dwa podciągi zbieżne do różnych granic to jest rozbieżny;

5) Ciąg ograniczony z góry (z dołu) i monotonicznie rosnący (malejący) jest zbieżny do kresu górnego (dolnego).

17. Definicja funkcji różnowartościowej, na zbiór i odwrotnej. Funkcje odwrotne do funkcji trygonometrycznych (rys).

Funkcję
nazywamy:
a) różnowartościową
;

b) na (zbiór Y)
;

c) wzajemnie jednoznaczną
gdy jest różnowartościowa i jest na
.

Funkcją odwrotną do funkcji wzajemnie jednoznacznej
nazywamy funkcję
taką, że
.

Funkcje odwrotne do funkcji trygonometrycznych:
a) Funkcja odwrotna do funkcji
to funkcja
.

b) Funkcja odwrotna do funkcji
to funkcja
.

c) Funkcja odwrotna do funkcji
to funkcja
.

d) Funkcja odwrotna do funkcji
to funkcja
.

18. Funkcje hiperboliczne i funkcje do nich odwrotne (rys).

Funkcję
określoną wzorem
nazywamy sinusem hiperbolicznym.

Funkcję do niej odwrotną oznaczamy i określamy następująco:
.

Funkcję
określoną wzorem
nazywamy cosinusem hiperbolicznym.

Funkcja ta jest parzysta i nie jest wzajemnie jednoznaczna, a więc nie istnieje do niej funkcja odwrotna.

Natomiast do funkcji
istnieje funkcja odwrotna, którą oznaczamy i określamy następująco:
.

Funkcję
określoną wzorem
nazywamy tangensem hiperbolicznym.

Funkcja ta jest nieparzysta, rosnąca, ograniczona i wzajemnie jednoznaczna.

Funkcję do niej odwrotną oznaczamy i określamy następująco:
.

Funkcję
określoną wzorem
nazywamy cotangensem hiperbolicznym.

Funkcja ta jest nieparzysta, przedziałami malejąca i wzajemnie jednoznaczna.

Funkcję do niej odwrotną oznaczamy i określamy następująco:
.

19. Definicja granicy funkcji w sensie Heinego. Obliczyć z definicji granicę np.
    .

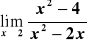
Def. Heinego:

Mówimy, że funkcja f ma w punkcie skupienia
dziedziny D granicę równą g, co zapisujemy
.

Definicja Heinego obejmuje 9 przypadków.

20. Definicja ciągłości funkcji. Własności funkcji ciągłych. Zbadać ciągłość funkcji (przykład).

Mówimy, że funkcja f jest w punkcie skupienia
ciągła wtedy i tylko wtedy, gdy
.

Mówimy, że funkcja f jest w punkcie skupienia
:

a) lewostronnie ciągła
gdy
;

b) prawostronnie ciągła
gdy
.

Funkcja f jest ciągła w punkcie
wtedy i tylko wtedy, gdy jest ciągła lewostronnie i prawostronnie w punkcie
.

Elementarne własności funkcji ciągłych:

1) Suma, różnica, iloraz, iloczyn funkcji ciągłych jest funkcją ciągłą;

2) Złożenie funkcji ciągłych jest funkcją ciągłą;

3) Funkcja odwrotna do funkcji ciągłej jest funkcją ciągłą.

Uwaga: Funkcje elementarne takie jak wielomiany, funkcje wymierne, wykładnicze, logarytmiczne, trygonometryczne, hiperboliczne itp. są funkcjami ciągłymi w swoich neutralnych dziedzinach.

Funkcje otrzymane z funkcji elementarnych przez dodawanie, odejmowanie, mnożenie, dzielenie, składania, odwracanie, też są ciągłe w swoich naturalnych dziedzinach.

UWAGA1: Prawie każde polega na podaniu definicji i rozwiązaniu przykładowego zadania - oczywiście zadań nie rozwiązywałem.

UWAGA2: Brakuje rysunków (uwaga do tych najbardziej spostrzegawczych).

Strona 8 z 8

---