Paweł Grzegrzółka AiR 1
Grzegorz Barnik AiR 1
ĆWICZENIE 6
Komputerowe wspomaganie analizy i syntezy układów sterowania
Liniowe układy jedno- oraz wielowymiarowe
1.a) Analiza obiektu przed korekcją bez pętli sprzężenia:
Obliczając transmitancje obiektu za pomocą przekształceni blokowych otrzymaliśmy poniższy wynik:
71,43( 0,1s+1)
G0(s) = ————————————————————
0,005s4 +0,5172s3 +4,91s2 +99,43s +41,43
czyli transmitancję o jednym zerze :
s = -10
i czterech biegunach :
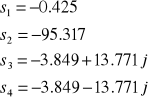
czas ustalania odpowiedzi skokowej
![]()
czasy narastania odpowiedzi skokowej
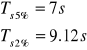
ustalona wartość odpowiedzi skokowej
![]()
Odpowiedź układu na skok jednostkowy:
Jak widać obiekt ten jest stabilny i nie posiada przeregulowania.
Charakterystyki Bodego (Amplitudowa i Fazowa)
Charakterystyka Nyquista
Zakłócenia
Warto zauważyć, że obiekt przy wprowadzeniu zakłócenia skokowego (przy braku sygnału wejściowego) eliminuje je, posiada stały uchyb pozycyjny:
Jak można się spodziewać dla zakłócenia „rampa” obiekt będzie miał nieskończony uchyb:
1.a) Analiza obiektu przed korekcją z zamkniętą pętlą sprzężenia zwrotnego
Obiekt z zamknięta jednostkową pętlą sprzężenia zwrotnego posiada następująca transmitancję:
71,43( 0,1s+1)
Gz(s) = ———————————————————
0,005s4 +0,5172s3 +4,91s2 +106,6s +112,9
czyli transmitancję o jednym zerze :
s = -10
i czterech biegunach :
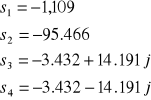
układ jest stabilny dla
-0,58 < k < 15.848
czas ustalania odpowiedzi skokowej
![]()
czasy narastania odpowiedzi skokowej
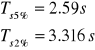
ustalona wartość odpowiedzi skokowej
![]()
zapas fazy
![]()
zapas wzmocnienia
![]()
uchyb
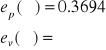
Odpowiedź układu na skok jednostkowy:
Jak widać obiekt ten jest stabilny i nie posiada przeregulowania.
Wykres linii pierwiastkowych:
Charakterystyki Bodego (Amplitudowa i Fazowa)
Charakterystyka Nyquista
1.b) Projektowanie regulatora metodą linii pierwiastkowych
Założenia:
- regulator PID
- zapas fazy 600
- czas ustalania dla strefy nie większy niż 0.5 s
- osiągnięcie możliwie maksymalnego wzrostu dokładności
Nasz układ wraz ze sterownikiem będzie odpowiadał poniższemu schematowi:
gdzie:
Gp(s) to transmitancja obiektu
Gc(s) to transmitancja regulatora PID :![]()
Czyli transmitancja całego układu wraz z pętlą jednostkowego sprzężenia zwrotnego wynosi:
![]()
W celu łatwej interpretacji i obliczeń zakładam, że o własnościach dynamicznych zamkniętego układu sterowania decyduje para dominujących, sprzężonych biegunów zespolonych transmitancji operatorowej układu, które odpowiedni są równe:
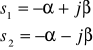
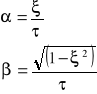
gdzie:
ξ - jest współczynnikiem tłumienia układu, zależnym od zapasu fazy w następujący sposób:
![]()
τ - jest określone w następujący sposób:
![]()
Obliczając dla wymagań naszego układu powyższe wielkości otrzymujemy:
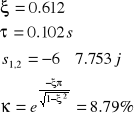
Na podstawie obliczonych biegunów możemy wyznaczyć parametry potrzebne do dalszej analizy:
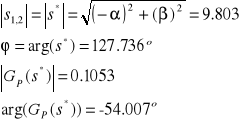
Obliczanie współczynników kp ki kd
Do wyznaczenia współczynników sterownika PID przyjęliśmy, że układ posiada zerowe wzmocnienie przyśpieszeniowe, a jego wzmocnienie prędkościowe będzie możliwie najmniejsze przy zachowaniu najkorzystniejszych parametrów.
ka = 0
kv = 0.3
obliczając wzmocnienie prędkościowe:
![]()
otrzymujemy pierwszy z parametrów:
![]()
dwa pozostałe obliczamy ze wzorów:
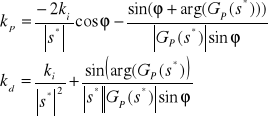
Wyliczone parametry sterownika PID:
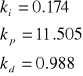
Odpowiedź układu ze sterownikiem PID:
Parametry zaprojektowanego układu:
czas ustalania odpowiedzi skokowej
![]()
czasy narastania odpowiedzi skokowej
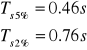
ustalona wartość odpowiedzi skokowej
![]()
zapas fazy
![]()
uchyb
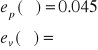
nieograniczony zapas wzmocnienia
Charakterystyki Bodego
Wykres Nyquista:
Wykres linii pierwiastkowych:
Odpowiedź układu w przypadku zakłóceń w postaci skoku i braku sygnału wejściowego :
Układ zaprojektowany różni się nieznacznie od specyfikacji, jest to związane z przybliżeniami wynikającymi z metody linii pierwiastkowych.
1.c) METODA ZIEGLERA - NICHOLSA PIERWSZEGO RODZAJU
Metoda ta opiera się na analizie kształtu początkowego fragmentu odpowiedzi skokowej
obiektu sterowania. W metodzie tej transmitancje obiektu aproksymuje się do postaci:
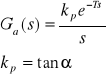
α - maksymalne nachylenie stycznej do odpowiedzi skokowej obiektu;
T - moment w której ta styczna przecina oś czasu
Natomiast transmitancja sterownika dana jest wyrażeniem:
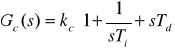
Odczytując wartości z wykresu odpowiedzi skokowej obiektu otrzymujemy następujące parametry:
![]()
Korzystając z poniższej tabeli w celu obliczamy odpowiednie parametry sterowników
Sterownik |
kc |
Ti |
Td |
P |
4.026 |
∞ |
0 |
PI |
3.623 |
0.198 |
0 |
PID |
4.831 |
0.12 |
0.03 |
Sterownik P:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
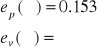
Sterownik PI:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
![]()
Sterownik PID:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
![]()
1.c) METODA ZIEGLERA - NICHOLSA DRUGIEGO RODZAJU
Jest metodą nastawiania sterowników według parametrów drgań granicznych.
Zakłada się, że w układzie sterowania ze sterownikiem typu P poprzez nastawienie wartości
wzmocnienia tego sterownika wzbudzone zostają okresowe drgania, gdzie:
kg - wzmocnienie sterownika wywołujące określone drgania;
Tg - okres tych drgań;
Jak zmierzyliśmy na początku obiekt jest stabilny do wartości k =15.848, i w programie CC za pomocą polecenia margins mierzymy Tg=3.098s
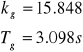
Tak jak metodzie pierwszego rodzaju tak i teraz do obliczenia poszczególnych parametrów sterowników posłuży nam poniższa tabelka:
Otrzymujemy zatem następujące wyniki:
Sterownik |
kc |
Ti |
Td |
P |
7.848 |
∞ |
0 |
PI |
7.132 |
3.463 |
0 |
PID |
9.509 |
1.549 |
0.387 |
Sterownik P:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
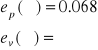
Sterownik PI:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
![]()
Sterownik PID:
odpowiedź skokowa:
czasy narastania odpowiedzi skokowej
![]()
uchyb
![]()
2. ANALIZA OBIEKTU DANEGO MODELEM STANOWYM
Zadany obiekt do analizy ma postać:

2.1 ANALIZA OBIEKTU
Zadany obiekt jest typu SIMO, posiada 1 wejście i 3 wyjścia, w związku z czym analizujemy układ dla każdego wyjścia z osobna, co prowadzi do rozbicia macierzy na 3 wiersze i analizy takiej postaci obiektu. Jednakże należy zauważyć, że w naszym przypadku transmitancje dla różnych wejść różnią się niewiele jedynie położeniem zer układu otwartego, co nie wpływa na wyniki analizowanych przez nas wielkości, dlatego analizę przeprowadziliśmy tylko dla Wy-1.
ANALIZA DLA WY-1:
Aby dokonać analizy wstępnej obiektu, korzystając z programu CC sprowadziliśmy powyższy model stanowy do postaci CCF (kanonicznej formy sterowalnej) i na jej podstawie określiliśmy transmitancję obiektu, która przedstawia się następująco:
![]()
Aby dokonać analizy wstępnej obiektu, korzystając z programu CC wyznaczyliśmy bieguny odpowiadające modelowi P:
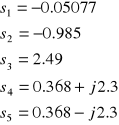
Zatem ponieważ występują bieguny, które leżą w otwartej prawej półpłaszczyźnie, stwierdzamy, że układ jest niestabilny. Zamykając układ jednostkową pętlą ujemnego sprzężenia zwrotnego od wyjścia uzyskujemy transmitację układu zamkniętego:
![]()
Wykonując po raz kolejny test Routha uzyskujemy bieguny:
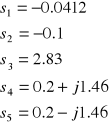
Zamknięty układ (wciąż niestabilny) odpowiada na skok jednostkowy w następujący sposób:
Jak widać zastosowanie ujemnego sprzężenia zwrotnego od wyjścia nie ustabilizuje obiektu. Zatem nie ma sensu określanie wskaźników odpowiedzi tego układu. Możemy jednak określić na podstawie zadanego modelu stanowego obiektu , czy układ jest sterowalny i/lub obserwowalny, gdzie obserwowalność i sterowalność obiektu jest warunkiem koniecznym do wyznaczenia wektora sprzężeń od stanu i wektora wzmocnień obserwatora.
Test Sterowalności:
Sterowalność obiektu wyznacza się określając wyznacznik z macierzy skonstruowanej na podstawie macierzy A oraz B:
![]()
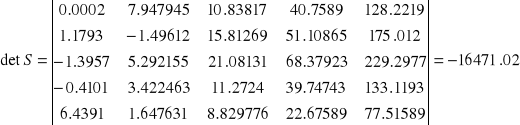
Zatem obiekt jest sterowalny.
Test Obserwowalności:
Obserwowalność obiektu wyznaczymy na podstawie macierzy V wyznaczonej w oparciu o macierze A i C:
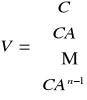
Obiekt jest także obserwowalny.
2.2 SYNTEZA STEROWANIA ZE SPRZĘŻENIEM OD STANU
Ponieważ objęcie obiektu ujemnym, jednostkowym sprzężeniem zwrotnym nie ustabilizowało obiektu,
zamiast tego zastosujemy odpowiednie sprzężenia od stanów przesuwając bieguny obiektu leżące w otwartej prawej półpłaszczyźnie na „lustrzane” pozycje w lewej półpłaszczyźnie zmiennej zespolonej s.
Opierając się na równaniu charakterystycznym obiektu z niewiadomymi współczynnikami wektora k, związanego z wejściem w następujący sposób:
![]()
uzyskuje się równanie charakterystyczne o postaci:
![]()
oczekiwane równanie charakterystyczne jest następujące:
![]()
Jesteśmy wstanie wyznaczyć wektor sprzężeń stanów K :
a) na podstawie przyrównania współczynników przy odpowiednich potęgach:
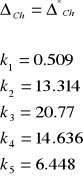
b) natomiast obliczenia w programie CC dały w rezultacie wektor K o współczynnikach:
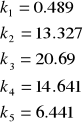
Obiekt z uwzględnieniem sprzężenia od stanów jest stabilny i ma postać:
![]()
Oto odpowiedź badanego układu (otwartego) po uwzględnieniu sprzężenia od stanów:
Natomiast poniżej przedstawiona jest odpowiedź układu jak powyżej ale z zamkniętą pętlą sprzężenia od wyjścia:
2.3 SYNTEZA OBSERWATORA PEŁNEGO RZĘDU
Ponieważ analizowany obiekt jest obserwowalny, co wykazaliśmy w punkcie 2.1, więc istnieje możliwość zaprojektowania obserwatora stanu. Uchyb estymacji stanu będzie dążył asymptotycznie do zera, wtedy i tylko wtedy, gdy wartości własne macierzy [A - LCT] będą leżały w lewej półpłaszczyźnie zmiennej zespolonej s. Projekt obserwatora stanu sprowadza się zatem do wyznaczenia wektora L. Należy przy tym pamiętać, że obserwator powinien być szybszy od obiektu, czyli jego bieguny powinny znajdować się w większej odległości od początku układu współrzędnych w głąb lewej półpłaszczyzny, niż bieguny obiektu.
Zakładamy, że żądanymi biegunami obserwatora są punkty: (-1,-1,-1,-2,-5)
Zatem dla takich biegunów obserwatora, wektor wzmocnień tego obserwatora, wyznaczony przy pomocy programu CC poleceniem POLE PLACEMENT, przedstawia się następująco:
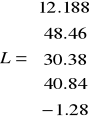
Takie wartości wzmocnienia obserwatora zapewniają położenie wartości własnych macierzy [A - LCT] w lewej półpłaszczyźnie.
2.4 SYNTEZA STEROWANIA ZE SPRZĘŻENIEM OD ESTYMATY STANU
Sprzężenie od estymaty stanu polega na zaprojektowaniu takiego wektora sprzężeń który będzie sprzęgał stany estymowane przez obserwator (takie postępowanie jest uzasadnione wtedy, gdy nie wszystkie stany obiektu są dostępne). I tak:
Model sterowanego obiektu:
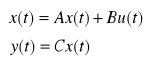
Model obserwatora:
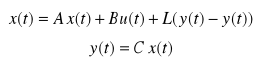
Błąd estymacji stanu:
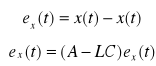
Model zamkniętego układu:
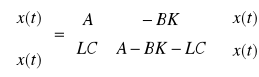
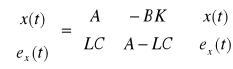
Jeżeli przyjmie się, że układ jest sterowany sygnałem:
![]()
(sprzężenie jest od estymaty stanu, a nie bezpośrednio od stanu obiektu), to po odpowiednich obliczeniach w programie CC, uzyskuje się następujący wektor wzmocnień sprzężeń od estymat stanów:
![]()
2.5 SYNTEZA STEROWANIA OPTYMALNEGO ZE WZGLĘDU NA
KWADRATOWE WSKAŹNIKI JAKOŚCI
Synteza ta opiera się na znalezieniu optymalnego sterowania u*(t), przy czym:
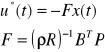
przy czym macierz P jest dodatnio półokreślona i ma następujące własności:
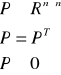
I macierz tą wyznaczamy rozwiązując równanie Riccatiego:
![]()
gdzie:
Q - macierz jednostkowa;
R - jest skalarem: R=1;
Opierając się na obliczeniach w programie CC, po przyjęciu kilku wartości ![]()
uzyskaliśmy następujące wartości wektora statycznego, liniowego sprzężenia od stanu:
|
F |
||||
1 |
-128.4769 |
-149.6760 |
-31.5360 |
222.6808 |
620.8788 |
50 |
-125.2268 |
-144.1257 |
-26.5215 |
224.0201 |
616.3842 |
500 |
-125.1636 |
-144.0179 |
-26.4241 |
224.0461 |
616.2969 |
1000 |
-125.1601 |
-144.0119 |
-26.4187 |
224.0475 |
616.2921 |
-500 |
-125.1496 |
-143.9940 |
-26.4025 |
224.0518 |
616.2775 |
-1000 |
-125.1531 |
-144.0000 |
-26.4079 |
224.0504 |
616.2823 |
Czyli w ten sposób osiąga się zmodyfikowane równania stanowe obiektu, o postacie:
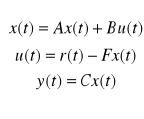
Gdzie przy określonym wektorze F układ osiąga maksymalną jakość sterowania ze względu na kwadratowe wskaźniki sterowania.
* * *
Wyszukiwarka
Podobne podstrony:
sterowanie - projekt 2 -2, Edukacja, studia, Semestr V, Sterowanie Analogowe, Laboratorium
TS - projekt, Edukacja, studia, Semestr VI, Teoria Sterowania, Projekt
Projekt 3, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Projekt, Projekt 3
Układ 8, Edukacja, studia, Semestr III, Metodyka Projektowania i Technika Realizacji, Laboratorium
Wybierz, Edukacja, studia, Semestr VIII, Kultura Języka Polskiego, CD1 - 2006 KJP-1 INFORMATYKA, KJP
materiały 5, Edukacja, studia, Semestr III, Inżynieria Materiałowa, Laboratorium, Materiały 5
Ćwiczenie projektowe nr 1, Studia Budownictwo polsl, I semestr, Hydrologia i hydraulika, projekt
przymiotniki-cwicz, Edukacja, studia, Semestr VIII, Kultura Języka Polskiego, CD1 - 2006 KJP-1 INFOR
materialy 6, Edukacja, studia, Semestr III, Inżynieria Materiałowa, Laboratorium, Materiały 6
czarodziej, Edukacja, studia, Semestr VI, Teoria Sterowania
Cw8LPCPS, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów, Ćwiczenia, Cwic
assembler 1, Edukacja, studia, Semestr IV, Architektura Systemów Komputerowych, Projekt, Projekt 1
więcej podobnych podstron