6. Opis zjawisk transportu:…

Dyfuzja w gazie czyli przenoszenie cząstek w kierunku obszarów o mniejszej koncentracji n Równanie dyfuzji

gdzie j_D gęstość strumienia cząstek, n - koncentracja cząstek. Równanie to znane jest pod nazwą prawa Ficka.

Przewodnictwo cieplne czyli transport energii, wskutek ruchu cząstek w kierunku obszaru o niższej T

gdzie j_Q jest gęstością strumienia ciepła, κ jest współczynnikiem przewodnictwa cieplnego.

Lepkość gazu polega na przenoszeniu pędu między warstwami gazu o różnych prędkościach

gdzie u jest prędkością warstwy.

Przewodnictwo elektryczne czyli przenoszenie ładunku elektrycznego w wyniku ruchu elektronów

gdzie przewodność elektryczna σ jest dana wyrażeniem. Wszystkie współczynniki transportu zależą od temperatury.

7. Ładunek i siła elektrostatyczna. Natężenie pola elekt. ładunku punktowego.

Oddziaływanie elektromagnetyczne- Pozwala wyjaśnić nie tylko zjawiska elektryczne ale też siły zespalające materię na poziomie atomów, cząsteczek. Przewodniki i izolatory. Doświadczenie z naładowaniem pręta metalowego i pręta szklanego. Zdolność izolacyjna stopionego kwarcu jest 10²⁵ razy większa niż miedzi.

Ładunek elekt. Porównajmy siłę grawitacyjną pomiędzy elektronem i protonem w atomie wodoru F = 3.61·10^-47 N z siła elektryczną pomiędzy nimi w tym samym atomie F = 2.27·10^-8 N.

To, że siły grawitacyjne dla "dużych" ciał dominują wynika stąd, że liczby protonów i elektronów są równe. Nie istnieje, żaden związek między masą i ładunkiem. W przeciwieństwie do masy ładunki "+" lub "-".

Zasada zachowania ładunku: Wypadkowy ładunek w układzie zamkniętym jest stały.

8. Zasada superpozycji pól elekt. Przykłady…

Siłę wypadkową obliczamy dodając wektorowo siły dwuciałowe. Dipol elektryczny składa się z dwóch ładunków oddalonych od siebie l. Sprawdzimy jaka siła jest wywierana na ładunek q

Z podobieństwa trójkątów

gdzie p = Ql jest momentem dipolowym.

9. Prawo Gaussa. Przykłady…

φ_całk = (Q₁/ε₀) + (Q₂/ε₀) = (Q₁ + Q₂)/ε₀

Całkowita liczba linii sił jest równa całkowitemu ładunkowi podzielonemu przez ε₀. Otrzymujemy więc prawo Gaussa

Strumień pola wychodzący z naładowanego ciała jest równa wypadkowemu ładunkowi podzielonemu przez ε₀. Jeżeli Q jest ujemne strumień wpływa do ciała.

Linie mogą zaczynać się i kończyć tylko na ładunkach a wszędzie indziej są ciągłe.

Rozważmy zamkniętą powierzchnię wewnątrz której Q_wewn. = 0, a linie sił pochodzą od ładunku na zewnątrz.

Całkowity strumień dzielimy na części

φ_całk = φ_ab + φ_bc + φ_cd + φ_da

Z rysunku widać, że

φ_ab = +2, φ_bc = +3, φ_cd = -7, φ_da = +2.

Tak więc φ_całk = +2 + 3 - 7 + 2 = 0

10,11. Zachowanie się ładunków przewodnika i dielektryka w zewn. polu elekt.

Większość ciał stałych można podzielić na przewodniki i izolatory. W izolatorze nadmiarowy ładunek może być rozmieszczony w całej objętości natomiast w przewodnikach swobodne elektrony będą się zbierały na powierzchni dopóty, dopóki nie wytworzy się pole równoważące pole zewnętrzne.

Rozpatrzmy dowolny w kształcie przewodnik. Wybierzmy powierzchnię zamkniętą tuż poniżej powierzchni przewodnika.

Zastosujmy prawo Gaussa do tej powierzchni

Wewnątrz przewodnika w dowolnym punkcie powierzchni S pole musi być równe zeru, bo inaczej elektrony poruszałyby się czyli

Zatem 0 = Q_wewn./ε₀ Q_wewn. = 0

Ładunek wewnątrz dowolnej zamkniętej powierzchni musi być równy zeru; cały ładunek gromadzi się na powierzchni.

12. Zast. prawa Gaussa- naładowana powierzchnia sfery.

Rozpatrzmy jednorodnie naładowaną powierzchnię kulistą.

W dowolnym punkcie sfery E  S

Zgodnie z prawem Gaussa: E(4πr²) = Q/ε₀

czyli

dla r > R (ładunek skupiony w środku sfery)

Dla r < R, E = 0

13. Zast. prawa Gaussa- jednorodnie naładowana kula.

Przewodniki - równoważne sferze bo ładunek na powierzchni. Izolator - równoważny szeregowi współśrodkowych sfer.

gdzie Q_wewn. = Q(r³/R³)

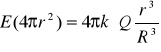
Wykres E w funkcji odległości od środka jednorodnie naładowanej kuli

14,15. Zast. prawa Gaussa- na zewn. i wewn. jednorodnie naładowanego długiego pręta.

Liczymy pole E w odległości r od jednorodnie naładowanego pręta o długości l >> r.

Wprowadzamy liniową gęstość ładunku λ.

Jako powierzchnię Gaussa wybieramy walec

zewn.

Z prawa Gaussa

E jest równoległe do wektora S i ma taką samą wartość w każdym punkcie powierzchni

zatem 2πrLE = 4πkLλ

wewn.

Wybieramy powierzchnię Gaussa o promieniu r < R.

Ładunek wewnątrz powierzchni Gaussa Q_wewn. = ρπr²L, gdzie ρ - gęstość objętościowa ładunku. Z prawa Gaussa otrzymujemy

E(2πrL) = 4πk(ρπr²L)

E = 2kρπr

ponieważ λ = ρπR²

więc

16. Zast.prawa Gaussa- jednorodnie naładowana płaszczyzna.

Obliczamy pole od nieskończonej jednorodnie naładowanej płaszczyzny.

Ładunek otoczony przez powierzchnię Gaussa jest równy Q_wewn. = σS, gdzie σ jest gęstością powierzchniową, a S powierzchnią podstawy walca.

Z prawa Gaussa 2ES = σS/ε₀

gdzie czynnik 2 odpowiada dwóm podstawom walca.

Zatem E = σ/2ε₀

17. Zast. prawa Gaussa- między dwoma naładowanymi płaszczyznami.

Pole wytwarzane przez płytę po lewej stronie jest równe E_minus = σ/2ε₀ i skierowane ku płycie.

Pole wytwarzane przez płytę po prawej stronie jest równe E_plus = σ/ε₀ i skierowane jest od płyty.

w obszarze I E_I = σ/2ε₀ + (- σ/2ε₀) = 0

-//-//- II E_II = -σ/2ε₀ + (- σ/2ε₀) = -σ/ε₀

-//-//- III E_III = (- σ/2ε₀) + σ/2ε₀ = 0

18. Energia potencjalna ładunku w polu elekt. Potencjał pola elekt. Różnica (nap.) potencj.

Różnica energii dla pola elekt. wynosi

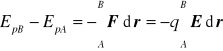
Możemy zdefiniować punkt zerowej energii potencjalnej dla ciała znajdującego się w nieskończoności.

Wtedy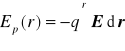

energia potencjalna jest równa pracy wykonanej przeciw sile elektrycznej

zatem energia potencjalna ładunków q i Q ma postać

Potencjał elektryczny- energia potencjalna na jednostkowy ładunek

Dla ładunku punktowego

Różnica potencjałów czyli napięcie U = praca na przeniesienie ładunku jednostkowego między tymi punktami

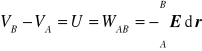
19. Obliczenie różnicy potencjałów na bazie rozkładu natężenia pola elekt.

Różnicę potencjałów pomiędzy środkiem i powierzchnią naładowanej powłoki kulistej wyznaczymy ze wzoru. Ponieważ E=0 wobec tego wzór ma postać: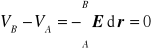

Oznacza to że zarówno w środku jak i na powierzchni jest ten sam potencjał.

Zatem

20. Obliczenie natężenia i potencjału pola elekt. dipola.

Rozważmy poniższy rys.

Moment dipolowy p = qL

Jeżeli r >> L to punkt P jest odległy od ładunku +q o: r - (1/2)Lcosθ

oraz od -q o: r + (1/2)Lcosθ

Całkowity potencjał jest sumą i ostatecznie dla r>>L otrzymujemy

21. Pojemność elekt. kondensatora. Energia pola elekt.

Kondensator - układ przewodników, który może gromadzić ładunek elektryczny.

Jednostka farad. 1F = 1C/1V.

Powszechnie stosuje się μF, nF, pF.

Energia pola elekt.

Początkowo nie naładowany kondensator ładuje się od 0 do napięcia U. Wtedy ładunek wzrasta od 0 do Q, gdzie Q = CU.

Praca zużyta na przeniesienie ładunku dq z okładki "-" na "+" wynosi dW = Udq

Energia pola wynosi

Dla kond. płaskiego

Podstawiamy Q do wzoru na energie

Jeżeli w jakimś punkcie przestrzeni jest pole E to możemy uważać, że jest tam zmagazynowana energia w ilości
na jednostkę objętości.

22. Def. prądu elekt. Zależność prądu od charakt. naładowanych cząstek…

Natężenie prądu elektrycznego

Jednostka: 1 amper, 1A

Gęstość prądu elektrycznego

W nieobecności zewnętrznego pola elektrycznego elektrony poruszają się we wszystkich kierunkach.

W zewnętrznym polu E uzyskują wypadkową prędkość unoszenia v_u.

Jeżeli n jest koncentracją elektronów to ilość ładunku Q jaka przepływa przez przewodnik o długości l w czasie t = l/v_u wynosi Q = nSle

Tak więc natężenie prądu wynosi

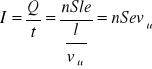
a gęstość prądu

gdzie ρ jest gęstością ładunku.

23. Prawo Ohma. Opór właściwy. Zjawisko nadprzewodnictwa.

Prawo Ohma jest słuszne pod warunkiem że utrzymuje się stała temp.

Z powyższego wzoru składowa stała p jest nazywana oporem właściwym.

Zależność oporu od temp. dla przewodników metalicznych jest pokazana poniżej

Jest to zależność liniowa ρ ~ T za wyjątkiem temperatur bliskich zera bezwzględnego.

Wtedy zaczyna odgrywać rolę tzw. opór resztkowy ρ₀ zależny w dużym stopniu od czystości metalu. Zjawisko nadprzewodnictwa możemy zaobserwować w metalach lub stopach w których dla niskich temp. mamy całkowity zanik oporu.

24. Straty mocy elekt. SEM. Źródła SEM.

Straty mocy elekt. P=UI

Aby utrzymać prąd potrzeba źródła energii elektrycznej. Np. baterie, akumul., generatory. Nazywamy je źródłami siły elektromotorycznej SEM. W takich źródłach jeden rodzaj energii jest zamieniany na drugi. SEM oznaczamy ε i definiujemy

gdzie W jest energią elektryczną przekazywaną ładunkowi q, gdy przechodzi on przez źródło SEM.

25. Siła, działająca na ładunki elekt. ze strony pola magnetycznego.

Siła magnetyczna to siła działająca w magnesach, elektromagnesach, cewkach, przekaźnikach, silnikach elekt. a nawet w telewizorach kineskopowych gdzie cewka odchyla wiązkę elektronów. Ogólnie możemy powiedzieć że siła magnetyczna to siła działająca miedzy poruszającymi się elektronami.

Na ładunek q nieporuszający się działa siła F_E=qE

Natomiast gdy ładunek porusza się z prędkością v całkowita siła wynosi F_E=qE+F_mag

gdzie F_mag=qv x B

Siła magnetyczna to:

Pole grawitacyjne

Pole elektryczne

Pole magnetyczne

26. Opis działania pola magnetycznego na poruszający się ładunek elekt. punktowy.

Pole magnetyczne

Wzór ten jest prawdziwy dla ruchu ładunku prostopadle do B ale siła F_magn zależy od kierunku v. Ta zależność od kierunku jest zapisana poprzez równanie wektorowe

F_magn jest zawsze prostopadłe do v.

Siła działa na ładunki w ruchu więc działa na cały przewodnik z prądem

F = ev_uB

W przewodniku o długości l znajduje się nSl elektronów, więc całkowita siła wynosi

oraz postać ogólna

27. Działanie pola magnetycznego na obwód z prądem.

W jednorodnym polu magnetycznym o indukcji B znajduje się ramka o bokach a i b. Przez ramkę płynie prąd o natężeniu I, a normalna do płaszczyzny ramki tworzy kąt  z polem B

Siły F_b działające na odcinki b znoszą się wzajemnie. Siły F_a działające na odcinki a też się znoszą ale tworzą parę sił dającą wypadkowy moment siły

Siła F_a wynosi

gdzie ab=S

S- wektor powieżchni

zatem

Pole magnetyczne działa więc na ramkę z prądem momentem skręcającym obracając ją. Położenie równowagi ramki występuje dla  = 0 tj. gdy ramka jest ustawiona prostopadle do pola B.

28. Pole magnetyczne. Źródła pola magnetycznego. Prawo Ampera.

Pole magnetyczne prezentujemy graficznie rysując tzw. linie pola magnetycznego. Zwrot wektora indukcji B wokół przewodnika wyznaczamy stosując regułę prawej ręki: Jeśli kciuk wskazuje kierunek prądu I, to zgięte palce wskazują kierunek B.

Związek między prądem i polem B jest wyrażony poprzez prawo Ampera.

gdzie μ₀ = 4π·10^-7 Tm/A, jest przenikalnością magnetyczną próżni.

Źródłami pola magnetycznego są np. solenoidy, cewki, pręty i płaszczyzny prądu.

29. Obliczenie indukcji pola magn. na zewn. nieskończonego przewodnika z prądem.

Chcemy obliczyć pole w odległości r od nieskończonego przewodnika z prądem.

W tym celu musimy zastosować prawo Ampera z którego wynika że dla konturu kołowego mamy

B2πr = μ₀I

Zatem pole na zewn. wynosi

30. Obliczenie indukcji pola magn. wewn. nieskończonego przewodnika z prądem.

Skoro wiemy że pole na zewn. pręta jest równe

dla r>R

Wobec tego dla pola wewn. r<R.

Wewnątrz konturu przepływa prąd i będący tylko częścią całkowitego prądu I

Podstawiając i do poniższego wzoru

B2πr = μ₀i

otrzymamy

Zatem pole wewn. wynosi

31. Obliczenie indukcji pola magn. wewn. solenoida z prądem.

Solenoid- cewka składająca się z dużej liczby zwojów nawiniętych obok siebie.

Skoro zwoje stykają się ze sobą to do obliczenia pola zastosujemy poniższy rys. stosując prawo Ampera.

Z czterech całek które otrzymujemy dla tego rys.

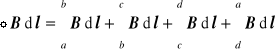
tylko pierwsza jest niezerowa (ponieważ dwie całki są równe 0 bo B ⊥ l i jedna jest równa 0 bo pole na zewn. jest równe zero)

Zatem pole wytwarzane przez ten solenoid wynosi

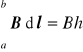
gdzie h jest długością odcinka ab.

32.Wyprow. wzoru na siłę oddziaływania miedzy dwoma równoległymi przewodnikami z prądem.

Mamy dane dwa równoległe przewodniki oddalone o d przez które płyną prądy I_a i I_b

Przewodnik a wytwarza pole

W polu tym znajduje się również przewodnik b w którym płynie prąd I_b. Zatem na odcinek o dł. l tego przewodnika działa następująca siła

Zwrot siły widać na rysunku.

33. Prawo Biota- Savarta. Obliczenie indukcji pola magn. na osi kołowego…

Rozkład prądów nie jest symetryczny i dlatego w tym przypadku nie możemy zastosować Prawa Ampera ponieważ otrz. bardzo trudną całkę do policzenia.

Natomiast Prawo Biota- Savarta pozwala obliczyć pole B z rozkładu prądów. Zasada postępowania jest następująca: dzielimy prądy na nieskończenie małe elementy i stosując Prawo Biota- Savarta obliczamy pole od takich elementów, a następnie sumujemy je żeby uzyskać wypadkowy wektor B.

Wartość liczbowa dB zgodnie z prawem Biota-Savarta wynosi

…

34. Zjawisko indukcji elektromagnetycznej. Prawo Faradaya. Reguła Lenza.

Zjawisko indukcji elektromagnetycznej polega na powstawaniu prądów elektrycznych w zamkniętym obwodzie podczas przemieszczania się względem siebie źródła pola magnetycznego i tego zamkniętego obwodu.

Prawo indukcji Faradaya stosuje się do trzech różnych sytuacji fizycznych:

1) Nieruchoma pętla, względem której porusza się źródło pola magnetycznego

2) Przewód w kształcie pętli porusza się w obszarze pola magnetycznego

3) Nieruchoma pętla i nieruchome źródło pola magnetycznego lecz zmienia się prąd

Prawo Faradaya

Reguła Lenza- prąd indukowany ma taki kierunek, że przeciwstawia się zmianie, która go wywołała.

Kierunek prądu indukowanego w pętli zależy od tego czy zbliżamy czy oddalamy magnes

35. Siła elektromotoryczna samoindukcji. Indukcyjność przewodnika.

Gdy natężenie prądu przepływającego przez cewkę zmienia się to zmienia się też strumień przez każdy zwój tej cewki więc indukuje się SEM. Tę siłę elektromotoryczną nazywamy siłą elektromotoryczną samoindukcji.

Wielkość Nφ jest całkowitym strumieniem zawartym w obwodzie i nosi nazwę strumienia skojarzonego. Strumień skojarzony jest proporcjonalny do prądu płynącego przez cewkę.

Nφ = LI

Stała proporcjonalności nazywana jest indukcyjnością i wynosi L = Nφ/I

Po zróżniczkowaniu otrzymujemy

ostatecznie

36. Wyprowadzenie indukcyjności cewki. Indukcyjność wzajemna.

Rozważmy transformator: strumień przechodzący przez cewkę 2 jest proporcjonalny do prądu płynącego przez cewkę 1. N₂φ₂₁ = M₂₁I₁

Stałą proporcjonalności M₂₁ nazywamy indukcją wzajemną.

Po różniczkowaniu otrzymujemy

Stąd

Jeżeli zmieniamy prąd I₂ to analogicznie

37. Wypr. zależności czasowych ładunku i prądu w ukł. RC w procesie przejściowym.

Sprawdzimy jaki prąd popłynie w obwodzie po zamknięciu wyłącznika.

Korzystamy z prawa Kirchoffa.

gdzie: I = dq/dt

zatem

stąd

Rysunki przedstawiają zależność q(t) oraz I(t).

Natężenie prądu przy rozładowaniu wynosi

38. Wypr. zależności czasowej nap. na cewce układu RL w procesie przejściowym.

Gdyby nie było cewki prąd osiągnąłby natychmiast wartość ε/R. Dzięki cewce w obwodzie pojawia się dodatkowo SEM samoindukcji ε_L. Z prawa Kirchoffa otrzymujemy

zatem

Rys. przedstawiają zależność u(t) na cewce

39. Energia i gęstość energii pola magnetycznego.

Z prawa Kirchoffa dla obwodu RL otrzymamy

po przekształceniu

czyli

Po scałkowaniu otrzymamy równanie na całkowitą energię magnetyczną

Gęstość energii dla solenoidu wynosi

Ponieważ

oraz wiemy że

i

zatem po połączeniu tych wzorów otrz. wyrażenie na gęstość energii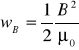

40. Drgania elektromagnetyczne. Opis ilościowy drgań w obwodzie LC.

Z prawa Kirchoffa U_L + U_C = 0

Ponieważ I = dq/dt więc

gdzie: q = q_mcosωt wtedy:

I = dq/dt = q_mωsinωt = I_msinωt

ω = (1/LC)^1/2

gdzie I_m = q_mω

U_L = - LdI/dt = - LI_mωcosωt

U_C = q/c = (q_m/C)cosωt

Ponieważ

LI_mω = Lq_mω² = Lq_m(1/LC) = q_m/C

widzimy, że amplitudy napięć są takie same.

41. Drgania elektromagnetyczne. Opis ilościowy drgań w obwodzie RLC.

Z prawa Kirchoffa

różniczkując po dt otrzymamy

Amplituda wynosi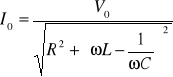

między napięciem i natężeniem prądu istnieje różnica faz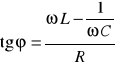

42. Prąd zmienny. Impedancja obwodu. Reaktancja pojem. i indukcyjna. …

Prąd zmienny- to taki prąd który pojawia się w obwodach prądu harmonicznego czyli w obwodach tych oprócz rezystora musi występować jeszcze cewka lub kondensator.

Impedancja obwodu- to suma wszystkich wartości elementów występujących w obwodzie przy czym dla cewki i kondensatora trzeba najpierw policzyć ich reaktancję.

Reaktancja pojemnościowa…

Reaktancja indukcyjna…

W obwodach RLC na kondensatorze prąd wyprzedza nap. o 90 st., natomiast na cewce prąd pozostaje za nap. o 90st.

43. Rezonans elektromagnetyczny w obwodzie RLC.

Warunek rezonansu

Niech będzie dany rys.

Taki obwód RLC znajduje się głowicy odb. radiowego, jego zadaniem jest dostrojenie pojemności do częstot. na której nadaje stacja radiowa.

Obwód ten może nam także posłużyć jako prosty wzm. nap. ponieważ przy dowolnym nap.wej. w warunkach rezonansu na wyj. (na kondensatorze) otrz. dużo większe nap. od wej.

44. Moc w obwodzie prądu zmiennego.

Moc w obwodzie prądu zmiennego liczy się podobnie jak dla prądu stałego trzeba tylko uwzględnić zmieniające się nap. i natężenie prądu.

Zatem

Więc moc w obwodzie RLC w dowolnej chwili t wynosi

1. Rozkład Maxwella prędkości cząsteczek gazu.

Rozkład prędkości cząsteczek dla gazu zawierającego N cząsteczek ma postać

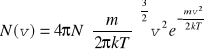
gdzie: N(v)dv jest liczbą cząstek o prędkościach z przedziału od v do v + dv. T - temperatura bezwzględna, k - stała Boltzmana, m - masa cząsteczki.

Rys. przedstawia rozkład Maxwella dla dwóch różnych temperatur.

gdzie -
prędkość średnia,
- prędkość średnia kwadratowa, v_p - prędkość najbardziej prawdopodobna.

Z równania widać, że rozkład prędkości zależy od masy cząsteczek.

2. Równanie Van der Waalsa dla gazów rzeczywistych.

Równanie stanu gazu doskonałego przy małych gęstościach. pV = nRT

Jeśli zaś mamy do czynienia z dużymi gęstościami gazu to cząstki zajmują część objętości dostępnej dla gazu. Wobec tego Van der Waals wprowadził zmienione równanie stanu gazu, które uwzględnia te czynniki. Jeżeli cząstki posiadają skończoną objętość to rzeczywista objętość dostępna dla cząstek jest mniejsza od objętości naczynia.

Niech v = V/n i otrzymujemy zmodyfikowane równanie stanu gazu p(v - b) = RT

Należy jeszcze uwzględnić siły międzycząstkowe i ostatecznie równanie ma postać

stałe a i b wyznaczamy doświadczalnie.

3. Opis cyklu Carnota. Sprawność silnika na bazie cyklu Carnota.

1) Gaz znajduje się w punkcie A. Cylinder stawiamy na zbiorniku ciepła i pozwalamy, żeby gaz rozprężył się izotermicznie do punktu B.

Gaz pobiera ciepło Q₁.

2) Cylinder stawiamy na izolującej podstawce i czekamy aż gaz rozpręży się adiabatycznie do punktu C. Temperatura spada do T₂.

3) Cylinder stawiamy na zbiorniku i sprężamy gaz izotermicznie do punktu D.

Z gazu do zbiornika przechodzi ciepło Q₂.

4) Cylinder stawiamy na izolującej podstawce i sprężamy adiabatycznie do punktu A.

Temp. gazu podnosi się do T₁.

Wypadkowa praca W wynosi W = Q₁ - Q₂

Sprawność silnika jest równa

4. Formułowania II zasady termodynamiki. Sprawność silnika cieplnego.

Druga zasada termodynamiki, różne sformułowania tej zasady:

1) Nie można zbudować perpetum mobile drugiego rodzaju.

2) Gdy dwa ciała o różnych temperaturach znajdą się w kontakcie termicznym, wówczas ciepło będzie przepływało z cieplejszego do chłodniejszego.

3) Żadna cykliczna maszyna cieplna pracująca pomiędzy temperaturami T₁ i T₂ nie może mieć sprawności większej niż (T₁ - T₂)/T₁.

4) W układzie zamkniętym entropia nie może maleć.

Silnik cieplny ma większą sprawność niż silnik Carnota.

5. Entropia. Termodynamiczna def. entropii. Entropia procesu adiabatycznego.

Entropia wiąże się z II zasadą termodynamiki.

Entropia jest miarą nieuporządkowania układu cząstek. Im większy jest stan nieporządku położeń i prędkości w układzie tym większe prawdop., że układ będzie w tym stanie.

Termodynamiczna def. entropii

Entropia S jest termodynamiczną funkcją zależną tylko od początkowego i końcowego stanu układu, a nie od drogi przejścia pomiędzy tymi stanami.

Entropia procesu adiabatycznego: jeżeli w układzie zachodzą procesy odwracalne to entropia jest stała, natomiast dla procesu nieodwracalnego entropia układu rośnie.

---