Wykład

Równania różnicowe. Transformata Z

Zalety sygnałów cyfrowych w stosunku do analogowych

1. Mała podatność na warunki atmosferyczne: temperaturę , wilgotność oraz na starzenie się materiału.

2. Brak interakcji pomiędzy sygnałami, redukcja kosztów

3. Brak dryfu parametrów

4. Wysoka pewność pomiarów

5. Złożone zadania mogą zostać wykonane przy niskich nakładach na sprzęt

6. Łatwość wprowadzania zmian w oprogramowaniu

Wady

1. Błędy wynikające ze skończonej precyzji (rozdzielczości)

2. Nagłe zmiany sygnałów z powodu ich dyskretnej postaci

3. Potrzeba znajomości złożonych metod inżynierskich

4. ograniczenia związane z czasem przetwarzania sygnału

5. Zwiększona podatność na błędy zasadnicze.

Transformata Z.

Rys. Sygnał ciągły i próbkowany

Sygnał wejściowy f(t) jest próbkowany co T chwil. W chwili T impulsator załącza się. Wówczas za impulsatorem będzie sygnał f*(t).

Jeżeli przyjmiemy oznaczenie

,

to otrzymany definicję transformaty Z:

Twierdzenie o wartości końcowej:

i początkowej:

.

Transmitancja Z.

Analogicznie do transmitancji Laplace'a

można zdefiniować transmitancję Z:

.

Dla z=e^jωT otrzymywana jest dyskretna transformata Fouriera. Transformata Z ma własności analogiczne do transformaty Laplace'a - jest liniowa i ma całkę splotu:

Jeżeli m=k-n , to k=m+n oraz

Ostatnie równanie stanowi iloczyn transformat Z sygnału wejściowego u(t) oraz odpowiedzi impulsowej obiektu h(t). Po wymnożeniu nawiasów otrzymywana jest odpowiedź obiektu na kolejne sygnały wejściowe

Sygnał wyjściowy z obiektu y(t) jest sumą odpowiedzi impulsowych :

G(z) jest transmitancja dyskretną obiektu.

Transformaty Z sygnałów.

Impuls jednostkowy

,

.

Skok jednostkowy

Korzystając z wzoru na sumę szeregu geometrycznego otrzymano

Sygnał linowo narastający.

Ostatecznie

.

Sygnał
,

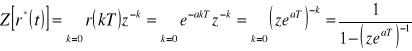
Sygnał sinusoidalnie zmienny
,

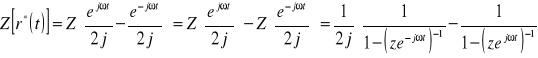
Tablica transformat Laplace'a i Z

Przykład. Posługiwanie się tablicą transformat.

Wyznaczyć transmitancję Z obiektu opisanego transformatą Laplace'a

Rozwiązanie

,

Stąd w dziedzinie czasu:

Porównanie odpowiedzi skokowych w Simulinku dla T=1,

Przykład. Zależność transformaty Z od położenia impulsatora.

Znaleźć transformatę Z w dwóch przypadkach

1. z impulsatorem pomiędzy dwoma obiektami G₁ i G₂

2. z impulsatorem za obiektami G₁ i G₂

Rozwiązanie. a)

,

Rozwiązanie b).

.

Ekstrapolator zerowego rzędu (Zero-order hold ZOH).

Wprowadzenie impulsu do obiektu może wywołać jego szybką odpowiedź, jeżeli występują człony rózniczkujące. Sposobem na uniknięcie tego jest zastosowanie ekstrapolatora zerowego rzędu. Sygnał z impulsatora jest podtrzymywany przez czas T w ekstrapolatorze zerowego rzędu.

Modelem matematycznym są dwa skoki jednostkowe przesunięte o T:

Przykład. Otwarty układ sterowania.

Znaleźć odpowiedź dyskretną obiektu.

Sygnał wejściowy r(t) Impulsator, r*(t)ekstrapolator p(t) Obiekt o transmitancji G₂(s) sygnał wyjściowy z obiektu c(t)

Rozwiązanie.

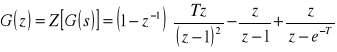
Z tw. Bezout:

Przykład. Zamknięty układ sterowania. Sygnał wyjściowy c(t) z poprzedniego przykładu wprowadzono poprzez ujemne sprzężenie zwrotne przed impulsator. Znaleźć odpowiedź skokową układu regulacji.

,

Stabilność.

Jeżeli pierwiastki równania charakterystycznego układu regulacji są ujemne, to układ regulacji jest stabilny. Stąd można otrzymać kryterium stabilności układu regulacji :

;

Stąd moduł z powinien być mniejszy od 1 (bo σ<0).

Przykład. Znaleźć współczynnik wzmocnienia K zapewniający stabilność układu regulacji danego transmitancją w układzie otwartym

Po zamknięciu układu regulacji

, stabilny, pierwiastki wewnątrz koła jednostkowego

, niestabilny, pierwiastki poza kołem jednostkowym.

Ostatecznie

impulsator

---