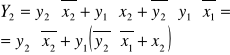Laboratorium Podstaw automatyki 2
DATA WYKONANIA:	ĆWICZENIE 11, 12	Rok akademicki
DATA ODDANIA:	ANALIZA I SYNTEZA KOMBINACYJNYCH ORAZ SEKWENCYJNYCH UKŁADÓW LOGICZNYCH	OCENA:

WSTĘP

Ćwiczenie podzielone jest na dwie części, które stanowią osobne zagadnienia w sprawozdaniu.

• analizę i syntezę kombinacyjnych układów logicznych

• analizę i syntezę sekwencyjnych układów logicznych

Powyższe zagadnienia opatrzone są cyframi rzymskimi poprzedzającymi kolejne nagłówki.

I. ANALIZA I SYNTEZA KOMBINACYJNYCH UKŁADÓW LOGICZNYCH

I.1. Cel ćwiczenia

Celem ćwiczenia jest sporządzenie schematu układu kombinacyjnego, który za pomocą minimalnej ilości bramek NAND spełni warunki zadane przez prowadzącego:

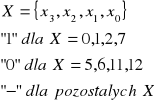
I.2. Wstęp teoretyczny

Każdą funkcję przełączającą można przedstawić w dwu postaciach kanonicznych:

sumy:

(wzór 1)

i iloczynu:

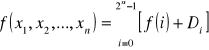
(wzór 2)

gdzie:

K_i - iloczyn pełny (iloczyn wszystkich argumentów funkcji, z negacjami lub bez),

D_i - suma pełna (suma wszystkich argumentów funkcji, z negacjami lub bez),

f(i) - wartość funkcji dla konkretnych wartości argumentów

Indeks „i” przy iloczynie pełnym K jest liczbą dwójkową (lub równoważną dziesiętną), utworzoną przez przyporządkowanie każdej zmiennej
symbolu 1, a zmiennej
symbolu 0. Tak więc, iloczynowi pełnemu
odpowiada indeks (11) czyli 3 i symbol K₃, iloczynowi pełnemu
indeks (010) czyli 2 i symbol K₂.

Indeks „i” przy sumie pełnej D tworzy się odwrotnie niż przy iloczynie pełnym, przyporządkowując 0 zmiennej
, a 1 zmiennej
. Sumie pełnej
odpowiada więc indeks (00) czyli 0 i symbol D₀, natomiast sumie pełnej
indeks (101), czyli 5 i D_5.

Ponieważ
oraz
, do przedstawienia funkcji według wzoru1 należy wypisać sumę tych K_i, dla których
.

Ponieważ
oraz
, do przedstawienia funkcji według wzoru2 należy wypisać iloczyn tych D_i dla których
.

I.3. Postaci kanoniczne funkcji

Tabela1. Tablica oczekiwanych stanów i x1 x2 x3 x4 y 0 0 0 0 0 1 1 0 0 0 1 1 2 0 0 1 0 1 3 0 0 1 1 - 4 0 1 0 0 - 5 0 1 0 1 0 6 0 1 1 0 0 7 0 1 1 1 1 8 1 0 0 0 - 9 1 0 0 1 - 10 1 0 1 0 - 11 1 0 1 1 0 12 1 1 0 0 0 13 1 1 0 1 - 14 1 1 1 0 - 15 1 1 1 1 -

Dla sumy (wzor 1): Dla iloczynu (wzór 2):

I.4. Minimalizacja funkcji metodą tablic Karnough'a

Tabela2. Minimalizacja dla jedynek

Tabela3. Minimalizacja dla zer

Minimalizacja funkcji przeprowadzona została metodą tablic Karnough'a.

Dla założonych obszarów jedynek, jak widać w tabeli2, funkcja powinna mieć dwa składniki. Większemu obszarowi odpowiada składnik
, ponieważ w tym obszarze x₁ oraz x₂ nie zmieniają się i wynoszą zero. Mniejszy obszar zawiera wartość nieokreśloną, którą przyjmujemy jako równą jeden. Składnik zminimalizowanej funkcji dla tego obszaru wynosi
.

Dla zer założono trzy obszary. Sposób rozpisania zminimalizowanej funkcji jest analogiczny; opis w punkcie I.2.

I.5. SPORZĄDZENIE UKŁADU ZA POMOCĄ BRAMEK NAND

W celu sporządzenia układu za pomocą bramek NAND posługujemy się wzorem otrzymanym z tabeli2 oraz wykorzystując prawo de Morgana
przekształcamy go do postaci:

Otrzymany układ:

I.6. SPRAWDZENIE ZAŁOŻEŃ UKŁADU

Tabela4. Sprawdzenie wartości otrzymanych z układu z wartościami założonymi na początku

i									yzałożone	yukładu
0	0	1	0	1	0	0	1	0	1	1
1	0	1	0	1	0	1	1	0	1	1
2	0	1	0	1	1	0	1	0	1	1
3	0	1	0	1	1	1	0	0	-	1
4	0	1	1	0	0	0	1	1	-	0
5	0	1	1	0	0	1	1	1	0	0
6	0	1	1	0	1	0	1	1	0	0
7	0	1	1	0	1	1	0	1	1	1
8	1	0	0	1	0	0	1	1	-	0
9	1	0	0	1	0	1	1	1	-	0
10	1	0	0	1	1	0	1	1	-	0
11	1	0	0	1	1	1	1	1	0	0
12	1	0	1	0	0	0	1	1	0	0
13	1	0	1	0	0	1	1	1	-	0
14	1	0	1	0	1	0	1	1	-	0
15	1	0	1	0	1	1	1	1	-	0

II.1. ANALIZA I SYNTEZA SEKWENCYJNYCH UKŁADÓW LOGICZNYCH

II.1. Cel ćwiczenia

Celem ćwiczenia jest sporządzenie schematu układu sekwencyjnego układu logicznego, który za pomocą minimalnej ilości elementów stykowych spełni warunki zadane przez prowadzącego w tablicy kolejności łączeń:

Tabela5. Tablica kolejności łączeń

Takty:			0	1	2	3	4	5	6	7
stan elementów	2^0	x1	-	+		-
		2^1	x2	-					+
		2^2	y1	-		+				-
		2^3	y2	-				+			-
stopień łączenia:			0	1	5	4	12	14	10	2

W tabeli zostały wyróżnione takty działania elementów Y₁ i Y_2. Pozostałe takty w cyklu pracy układu są taktami niedziałania.

II.2. Tablice Karnough'a.

III.3 SPORZĄDZENIE UKŁADU ZA POMOCĄ ELEMENTÓW STYKOWYCH

Rysunek2. Realizacja stykowa układu zadanego tablicą kolejności łączeń

1

---