WIP, ZIP, gr. 2
SPRAWOZDANIE
Z LABORATORIUM TECHNIKI CIEPLNEJ
Badanie przepływów płynów.
Wyznaczanie współczynnika lepkości cieczy.
Wykonali:
Chędoszko Arkadiusz
Olszewski Jakub
Pietruczuk Marcin
Pleńska Aneta
Podniesińska Martyna
Rojek Katarzyna
Rybacki Iwo
Szostek Anna
Wprowadzenie teoretyczne.
Przepływ to opis ruchu płynu, podstawowe pojęcie z zakresu kinematyki płynów.
W ujęciu ogólnym przepływ można scharakteryzować tzw. metodą Eulera przez podanie pola prędkości płynu, czyli zależności prędkości od współrzędnych przestrzennych i czasu.
Cieczą doskonałą nazywamy ciecz nieściśliwą, nielepką, inaczej: płyn idealny.
Pojęcie to stosuje się w hydrodynamice i aerodynamice do opisu laminarnych przepływów, przy dużych liczbach Reynoldsa.
Płyny rzeczywiste mają zdolność przyczepiania się do ścian przewodów, przez które przepływają lub też do przedmiotów, wokół których opływają. Zdolność ta nazywa się lepkością.
Lepkość.
Lepkość to opór wewnętrzny przeciw płynięciu. Lepkością nie jest opór przeciw płynięciu powstający na granicy płynu i ścianek naczynia. Lepkość jest jedną
z najważniejszych cech olejów.
Zgodnie z laminarnym modelem przepływu lepkość wynika ze zdolności płynu do przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi prędkościami. Różnice w prędkościach warstw są charakteryzowane w modelu laminarnym przez szybkość ścinania. Przekazywanie pędu zachodzi dzięki pojawieniu się na granicy tych warstw naprężeń ścinających. Wspomniane warstwy są pojęciem hipotetycznym, w rzeczywistości zmiana prędkości zachodzi w sposób ciągły (zobacz: gradient), a naprężenia można określić w każdym punkcie płynu. Model laminarny lepkości zawodzi też przy przepływie turbulentnym, powstający np. na granicy płynu i ścianek naczynia.
Dla przepływu turbulentnego jak dotąd nie istnieją dobre modele teoretyczne.
Płyn nielepki to płyn o zerowej lepkości.
Istnieją dwie miary lepkości:
Lepkość dynamiczna wyrażająca stosunek naprężeń ścinających do szybkości ścinania:
Jednostką lepkości dynamicznej w układzie SI jest: kilogram·metr-1·sekunda-1
Lepkość kinematyczna czasami nazywana też kinetyczną jest stosunkiem
lepkości dynamicznej do gęstości płynu:
Jednostką lepkości kinematycznej w układzie SI jest: metr2·sekunda-1
Jej nazwa pochodzi od tego, że jest wyrażona jedynie przez wielkości właściwe kinematyce.
Rodzaje przepływów:
Przepływ stacjonarny (ustalony) jest pojęciem uproszczonym zakładającym,
że przepływ w każdym punkcie obszaru zajętego przez ciecz nie zmienia się w czasie. Przy takim założeniu równania opisujące ruch płynu (Naviera-Stokesa i ciągłości przepływu) przybierają prostsze formy.
Podstawową zależnością opisującą wpływ sił na ruch płynu jest równanie Naviera-Stokesa.
gdzie: v - prędkość, b - siły masowe (np. grawitacja), ρ - gęstość płynu, p - ciśnienie,
ν - lepkość kinematyczna płynu
Lewa strona równia jest pochodną substancjalną prędkości płynu.
Przepływ laminarny (warstwowy) jest pojęciem stosowanym do określenia przypadku, gdy strumień stanowi zespół warstw przemieszczających się jedna względem drugiej bez ich mieszania, a prędkość w każdym punkcie jest jednoznacznie określona. Przy małych prędkościach przepływ cieczy przez gładką rurę jest laminarny, a ze względu na lepkość największa prędkość przepływu jest w środku - wzdłuż osi przekroju podłużnego rury.
Przepływ turbulentny (wirowy) jest określeniem ruchu warstw cieczy, podczas którego prędkość maksymalna przepływu cieczy przekroczy pewną charakterystyczną dla danego płynu wartość "krytyczną". Następuje wtedy mieszanie cieczy, w efekcie czego powstają wiry- stąd też określenie przepływu turbulentnego, który ze swej natury jest zmienny w czasie. Prędkość przestaje wtedy być wtedy prostą funkcją współrzędnych położenia.
Możliwe jest wprowadzenie uśrednionych wartości opisujących przepływ, a także średnich kwadratowych wartości ich odchyleń. Podejście to znacznie komplikuje równania przepływu. Jest też możliwe w przypadku turbulentnego przepływu nieustalonego. W przypadku płynu nielepkiego i przepływu bezwirowego, przepływ ustalony nosi nazwę przepływu potencjalnego ponieważ pole prędkości jest wtedy polem potencjalnym.
Równanie Bernoullego opisuje parametry płynu doskonałego płynącego w rurze (niekoniecznie materialnie istniejącej) o zmiennym przekroju. Wynika ono wprost z faktu zachowania objętości cieczy doskonałej (która jest nieściśliwa) i zasady zachowania energii mechanicznej.
Założenia:
ciecz jest nieściśliwa
ciecz nie jest lepka
przepływ stacjonarny i bezwirowy
gdzie:
E - energia jednostki masy płynu
ρ - gęstość cieczy
v - prędkość cieczy w rozpatrywanym miejscu
h - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna
g - przyspieszenie grawitacyjne
p - ciśnienie cieczy w rozpatrywanym miejscu
Poszczególne człony to: energia kinetyczna, energia potencjalna przyciągania ziemskiego, energia ciśnienia.
Energia jest stała tylko wówczas, kiedy element porusza się wzdłuż linii prądu.
Istnienie lepkości lub przepływu wirowego rozprasza energię, ściśliwość zmienia zależność prędkości przepływu od ciśnienia. Niestacjonarność przepływu wiąże się z dodatkowym ciśnieniem rozpędzającym lub hamującym ciecz.
Z równania Bernoullego dla sytuacji przedstawionej na rysunku zachodzi prawidłowość:
Rys. 1. Wpływ średnicy kanału na prędkość przepływu.
W rurze o mniejszym przekroju ciecz płynie szybciej (v1 > v2), w związku z tym panuje w niej mniejsze ciśnienie niż w rurze o większym przekroju. Ciecz płynąc w rurze o zmieniającym się przekroju ma mniejsze ciśnienie na odcinku, gdzie przekrój jest mniejszy.
Liczba Reynoldsa - jedna z liczb podobieństwa stosowanych w reologii. Przy jej pomocy można oszacować stosunek sił bezwładności do sił lepkości. Liczba Reynoldsa jest kryterium do wyznaczania charakterystyki przepływu wszelkich płynów nieściśliwych.
Gdzie:
l - wymiar charakterystyczny
v - prędkość charakterystyczna płynu
ρ - gęstość płynu
μ - lepkość dynamiczna
ν - lepkość kinematyczna
Liczba Reynoldsa charakteryzuje charakter przepływu. Dla przepływu płynu przez rurę,
gdzie za v przyjmuje się średnią prędkość przepływu, a za l średnicę rury,
zbadano doświadczalnie, że w przybliżeniu dla:
Re<2300 - przepływ laminarny (uporządkowany)
2300<Re<10000 - przepływ przejściowy (częściowo burzliwy)
Re>10000 - przepływ turbulentny (burzliwy)
Podane granice obszarów są umowne i zależą od cytowanych źródeł. Dla innych przepływów niż w rurach podanie podobnych granic jest również możliwe. Nie istnieją jednak ich uniwersalne wartości, ponieważ zależą od tego co zostanie uznane za "charakterystyczne" w odniesieniu do wielkości v i l (w przypadku płynów ściśliwych także ρ, a dla płynów nienewtonowskich μ).
Liczba ta nazwę swoją wzięła od Osborne'a Reynoldsa - irlandzkiego inżyniera,
który zaproponował jej stosowanie.
Wyznaczenie współczynnika lepkości dynamicznej.
Doświadczenie przeprowadzono z wykorzystaniem wiskozymetru Hopplera.
Opis aparatury:
Wiskozymetr Hopplera to urządzenie, które składa się z cylindra zawierającego szklaną rurkę pomiarową, której oba końce zamknięte są korkami i w której znajduje się ciecz. Całość zamocowana jest w obrotowym statywie, zawierającym zacisk sprężynowy, który służy do unieruchomienia cylindra podczas pomiarów. W rurce znajduje się kulka pomiarowa, której za pomocą stopera, mierzy się czas opadania między dwiema kreskami pomiarowymi zaznaczonymi na rurce (Rys. 2).
Rys. 2. Wiskozymetr Hӧpplera
Wykonanie ćwiczenia:
Po odpowiednim ustawieniu urządzenia, obracamy cylinder, aby sprowadzić kulkę
do górnego korka rury pomiarowej, następnie ustawiamy cylinder w pozycji pomiarowej, unieruchamiamy go za pomocą zacisku sprężynowego w dolnej części statywu
i stoperem mierzymy czas opadania kulki między skrajnymi kreskami pomiarowymi.
Pomiary wykonujemy pięciokrotnie.
Poniższa tabela 1 przedstawia uzyskane wyniki pomiarów:
Tabela 1. Wyniki pomiarów z wykorzystaniem wiskozymetru.
Lp. |
τ [s] |
1 |
125,78 |
2 |
15,86 |
3 |
15,21 |
4 |
15,75 |
5 |
15,65 |
Obliczenia.
Dane:
średnica kulki: d = 1,63 cm
masa kulki: Gkulki = 9,6 g
długość odcinka między kreskami: s = 10 cm
masa cylindra: G1 = 83,85 g
masa cylindra z cieczą: G2 = 97,11 g
objętość cylindra: V = 14 ml
d = 1,63 cm = 0,0163 m
s = 10 cm = 0,1 m
g ≈ 9,81 m/s2
Gkulki = 9,6 g = 0,0096 kg
r = 0,5·d = 0,5·0,0163 = 0,00815 m
![]()
![]()
Średni czas opadania kulki:
![]()
Prędkość opadania kulki:
![]()
G1 = 83,85 g
G2 = 97,11 g
V = 14 ml = 0,014 dm3
![]()
Współczynnik lepkości dynamicznej:
![]()
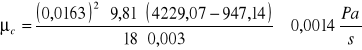
Współczynnik lepkości kinematycznej:
![]()
Błąd bezwzględny:
![]()
s
Błąd względny:
![]()
Wnioski.
Błędy wynikające z niedokładnego pomiaru czasu opadania kulki są spowodowane tym, że włączenie i wyłączenie stopera nie nastąpiło równocześnie z momentem przekraczania przez kulkę granicznych kresek.
Stwierdzono, że prędkość kulki wzrastała z każdym kolejnym pomiarem. Wzrost ten jest spowodowany zwiększeniem się temperatury cząsteczek tworzących ciecz badaną, co z kolei powstaje w wyniku tarcia kulki z cząsteczkami cieczy. Początkowo cząsteczki badanej cieczy nie tworzyły jednorodnej substancji, w związku z tym kulka na swej drodze napotkała duży opór, dlatego czas jej opadania miedzy kreskami, tak bardzo się wydłużył. Przy kolejnych pomiarach w jednorodnej już cieczy, opór znacznie się zmniejszył, więc opadanie kulki następowało szybciej.
Powstałe błędy dotyczą również złego ustawienia cylindra (zły kąt).
Wyznaczanie gęstości za pomocą areometru.
Opis aparatury:
Areometr to urządzenie służące do mierzenia gęstości cieczy, w którym wykorzystuje się siły wyporu z jaką ciecz działa na zanurzone w niej ciało stałe. Zbudowany jest z pustej szklanej rurki, której górna wydłużona część zaopatrzona jest w specjalną skalę, część dolna w postaci bańki wypełniona jest materiałem o dużej gęstości - śrutem, co pozwala na utrzymanie pozycji pionowej przyrządu zanurzonego w cieczy (Rys. 3).
Rys. 3. Klasyczny areometr obciążeniowy.
Wykonanie ćwiczenia:
Począwszy od pierwszego (najmniejszego) areometru kolejno zanurzamy je w badanych cieczach. Głębokość na jaką zanurza się dolna część areometru wynika z różnicy między ciężarem areometru a ciężarem wypartej przez areometr cieczy.
Uzyskane wyniki pomiarów przedstawia tabela 2.
Tabela 2. Wyniki pomiarów z wykorzystaniem aerometru.
Areometr |
skala |
Gestość [g/cm3] |
|
|
|
I cieczy |
II cieczy |
1 |
0,7 - 0,8 |
> |
> |
2 |
0,8 - 0,9 |
> |
> |
3 |
0,9 - 1,0 |
> |
1 |
4 |
1,0 - 1,1 |
0,098 |
|
Wypływa cieczy ze zbiornika.
Opis aparatury:
Ćwiczenie składa się z dwóch statywów, na których są umieszczone dwie butelki. Jedna z nich ma przekrój poprzeczny jednakowy na całej długości tzn. jest prostopadłościanem, a druga ma przekrój zmienny, tzn. w jednej z części jest walcem, a w drugiej stożkiem. Butelki są umocowane spodem do góry. Dna w tych butelkach są usunięte. W nakrętkach butelek są zrobione małe otwory, mające na celu umożliwienie wypływu cieczy. Zastosowany zbiorniki to butelka o jednakowym przekroju poprzecznym (kwadrat o boku 8cm) z otworem w nakrętce o średnicy 3mm (Rys. 4) oraz butelka o zmiennym przekroju: walca o podstawie koła o promieniu r = 4,2cm oraz stożka i otworze w nakrętce o średnicy 3mm (Rys. 5).
Wykonanie ćwiczenia:
Zatykając otwory w nakrętkach butelek nalewamy wodę, tak, by nalać ją aż po brzegi. Następnie odtykając otwory w nakrętkach mierzymy czas stoperem wypływu cieczy aż do opróżnienia zbiornika. Pomiary wykonujemy 5-krotnie.
Rys. 4. Butelka pomiarowa 1.
Rys. 5. Butelka pomiarowa 2.
Poniższa tabela przedstawia wyniki pomiarów:
Tabela 3. Wyniki pomiarów wypływu cieczy
Lp. |
τ [s] (przekrój stały) |
τ [s] (przekrój zmienny) |
1. |
75 |
900 |
2. |
76 |
902 |
3. |
75 |
906 |
4. |
76 |
905 |
5. |
75 |
906 |
Wyznaczenie współczynnika wypływu otworu w dnie dla obu zbiorników:
Zbiornik I
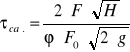
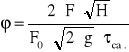
Dane:
![]()
g ≈ 9,81 m/s2
![]()
H=20cm=0,20m
Obliczenia:
![]()
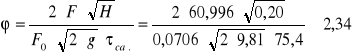
Dyskusja jednostek:
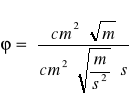
Stwierdzono, że wyliczona wartość jest bezwymiarowa.
Zbiornik II
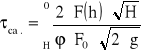
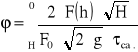
Dane:
![]()
g ≈ 9,81 m/s2
d=10,8cm
H1=14,5cm= 0,145m
H2=10cm= 0,1m
Obliczenia:
H= H1 + H2=0,145m +0,1 m= 0,245m
![]()
![]()
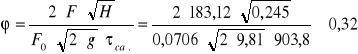
Dyskusja jednostek:
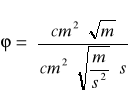
Stwierdzono, że wyliczona wartość jest bezwymiarowa.
Wyznaczenie błędów pomiarów.
Błędy niedokładnego pomiaru czasu opróżnienie zbiornika wynikają z niesynchronizowania włączenia stopera a odetkania otworu. A także zanieczyszczeniami zawartymi na powierzchni butelki lub znajdującymi się w wodzie.
Niedokładny pomiar wymiarów zbiornika spowodowany jest tym, że butelka nie była idealnym prostopadłościanem ani stożkiem i walcem. Butelka ta posiadała liczne wgłębienia, których nie uwzględnialiśmy w pomiarach. Błąd może być również spowodowany wykonywaniem pomiarów linijką, która jest niedokładnym urządzeniem pomiarowym.
Wyznaczenie błędu bezwzględnego i względnego pomiaru współczynnika wypływu otworu w dnie dla obu zbiorników.
Błąd bezwzględny:
Zbiornik I
![]()
Zbiornik II
![]()
Błąd względny:
Zbiornik I:
![]()
Zbiornik II:
![]()
Wartość ciśnienia działającego na powierzchnię lustra cieczy.
![]()
Zbiornik I
Dane:
H = 20cm=0,2m
g ≈ 9,81 m/s2
ρ = 1000 kg/m3
Obliczenia:
![]()
![]()
![]()
Zbiornik II
Dane:
H = 24,5cm=0,245m
g ≈ 9,81 m/s2
ρ = 1000 kg/m3
Obliczenia:
![]()
![]()
![]()
Dyskusja jednostek:
![]()
Współczynnik wypływu jest zależny od gęstości cieczy wypływającej( im większa gęstość tym większy współczynnik) oraz od wielkości otworu odpływowego. Na przykład biorąc pod uwagę wodę i oliwę, ich gęstości są różne. Oliwa ma większą wartości gęstości niż woda, więc jej czas wypływu ze zbiornika będzie dłuższy niż czas wypływu wody, zatem gęstość cieczy jest zależna od czasu opróżniania zbiornika.
Całkowity czas wypływu ze zbiornika prostopadłościennego pionowego:
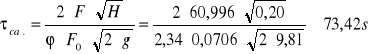
s
Wnioski:
Współczynnik wypływu otworu w dnie zbiornika I wyniósł 2,34 natomiast współczynnik wypływu otworu w dnie zbiornika II wyniósł 0,32. Współczynnik ten jest zależny od gęstości wypływającej cieczy (im większa gęstość tym większy jest współczynnik). Zależy on również od wielkości otworu odpływowego. Wartość ciśnienia działającego na powierzchnię lustra wody wyniosła dla pierwszego zbiornika wyniosła: -1962Pa, a dla drugiego zbiornika: -2403Pa (podciśnienie).Wartości te mogły być obarczone błędami spowodowanymi złymi pomiarami zbiornika (szczególnie otworu), ponieważ nie używamy profesjonalnych przyrządów pomiarowych tylko linijki, która mogła wykazać złą wartość. Błędy mogą wynikać również z niedokładności pomiaru czasu wypływu wody ze zbiorników.
Badanie oporów przepływów.
Cel ćwiczenia:
Celem ćwiczenia było wyznaczenie charakteru przepływu cieczy nieściśliwej w poszczególnych odcinkach przewodu, oraz oporów liniowych i miejscowych jej przepływu.
Opis aparatury:
Aparatura zbudowano z otwartego zbiornika na wodę, z którego wyprowadzony został zespół kanałów przepływowych (rys. 1, rys. 2,rys. 3) składających się z rurek o średnicy ½”, kolanek i trójnika o tej samej średnicy, oraz rozszerzenia o średnicy ¾”.
Rys. 6. Schemat układu przepływu - rzut izometryczny
Rys. 7. Schemat układu przepływu - rzut z przodu
Rys. 8. - Schemat układu przepływu - widok z boku
Przebieg ćwiczenia:
Początkowym pomiarem, było wyznaczenie temperatury i ciśnienia powietrza w laboratorium. Temperatura wody w zbiorniku, zgodnie ze wskazaniem prowadzącego, została przyjęta jako temperatura otoczenia.
Wypływ cieczy ze zbiornika następował po otwarciu zaworu głównego, oraz jednego lub dwóch zaworów wylotowych. Ustalenie warunków układu następowało po odkręceniu wszystkich zaworów, do momentu wypływu cieczy z obydwu wylotów. Następnie zakręcono zawory wylotowe i poczekano do momentu ustalenia się poziomu cieczy w zbiorniku.
Objętość cieczy, która opuściła układ przepływu wyznaczono za pomocą wyskalowanego pojemnika. Czas przepływu cieczy zmierzono przy użyciu stopera. Ubytek cieczy w zbiorniku głównym uzupełniano wodą zebraną do naczynia pomiarowego po każdorazowym pomiarze. Każda seria pomiarów składała się z pięciu powtórzeń, co umożliwia wyeliminowanie błędów pomiarowych grubych.
Wyniki pomiarów dla pierwszej serii pomiarów - wypływ cieczy po otwarciu jednego zaworu wylotowego przedstawia Tabela 1.
Tabela 4. Wyniki pomiarów dla pierwszej serii pomiarów - wypływ cieczy po otwarciu jednego zaworu wylotowego
Lp. |
Czas [s] |
Objętość cieczy [ml] |
1 |
17,48 |
630 |
2 |
19,57 |
630 |
3 |
21,74 |
700 |
4 |
22,4 |
710 |
5 |
18,87 |
630 |
Wyniki pomiarów dla drugej serii pomiarów - wypływ cieczy po otwarciu dwóch zaworów wylotowych przedstawia Tabela 2.
Tabela 5. Wyniki pomiarów dla drugej serii pomiarów - wypływ cieczy po otwarciu dwóch zaworów wylotowych
Lp. |
Czas [s] |
Kanał wylotowy lewy [ml] |
Kanał wylotowy prawy [ml] |
1 |
16,54 |
780 |
50 |
2 |
24,11 |
650 |
300 |
3 |
18,56 |
470 |
290 |
4 |
24,33 |
640 |
360 |
5 |
25,15 |
880 |
120 |
6 |
18,83 |
500 |
300 |
Temperatura wody wynosi 21,2°C, ciśnienie powietrza 1006hPa.
Obliczenia dla pierwszej serii pomiarowej.
Równanie Bernoullego, przedstawiające charakterystykę przepływu w układzie: :
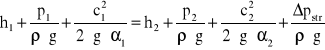
,gdzie:
h1 = 100mm = 0,1m - wysokość słupa cieczy w zbiorniku,
h2 ≈ 0,
p1 = p2, przyjęto równe ciśnienia dla zbiornika i układu przepływu,
c1 ≈ 0, prędkość przepływu wody w zbiorniku.
c2 - średnia prędkość przepływu wody w układzie.
Kanał przepływowy składał się z odcinków o następujących długościach:
l1=280mm = 0,28m,
l2=230mm = 0,23m,
l3=310mm = 0,31m,
l4=145mm = 0,145m,
l5=1025mm = 1,025m - odcinek o średnicy ¾”,
l6=535mm = 0,535m,
l7=160mm = 0,16m,
l8=305mm = 0,305m,
l9=1495mm = 1,495m,
l10=670mm = 0,67m.
długość całkowita rur o średnicy ½” Δl1=4,13m, a o średnicy ¾” Δl2=1,025m
Wyznaczenie c2 dla pierwszej serii pomiarowej jako średniej arytmetycznej z prędkości dla kolejnych pomiarów.
![]()
Należy uwzględnić, że przy przepływie z otwartym jednym zaworem wylotowym udział długości rurki o średnicy ¾” w stosunku do całkowitej długości kanału przepływowego wynosi w przybliżeniu 20%. Wraz ze zmianą powierzchni przekroju rurki, zmienia się prędkość przepływu. Prędkość przepływu przez szerszy kanał wyznaczono z równania stałości przepływu:
c2a * F1 = c2b * F2
, czyli
,
c2a jest średnią arytmetyczną z prędkości przepływów wyznaczonych w kolejnych pomiarach:
i ostatecznie
c2a = 0,26 m/s,
więc:
c2b = 0,15 m/s,
Wyznaczenie charakteru przepływu.
Charakter przepływu opisuje liczba charakterystyczna Reinoldsa Re, wyznaczona zgodnie z tablicą 8.
![]()
gdzie:
c2 - średnia prędkość przepływu cieczy,
d - srednica wewnętrzna kanału,
ν - współczynnik lepkości kinematycznej płynu, odczytany z tabeli 18 dla t=20°C, czyli temperatury wody; ν=1,006 * 10-6 [m2/s]
, czyli:
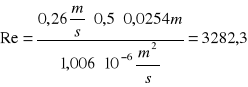
Dla wskazanych danych liczba Reinoldsa wynosi:
![]()
,
co oznacza, że przepływ ma charakter burzliwy.
Natomiast dla przekroju grubszego:
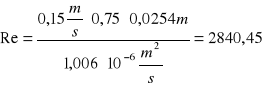
Dla wskazanych danych liczba Reinoldsa wynosi:
![]()
,
co oznacza, że przepływ jest w dalszym ciągu burzliwy.
Następnie wyznaczono empiryczny współczynnik liniowych oporów przepływu z tablicy 5
![]()
,
Gdzie współczynniki a, b, n przyjęto z równania Blassiusa:
a=0, b=0,3164, n=0,25
Po podstawieniu do wzoru otrzymano wartość współczynnika λ dla wąskiej rurki:
![]()
oraz dla szerokiej:
![]()
Otrzymaną wartość współczynnika wstawiono do wzoru Darcy'ego-Weisbacha opisującego liniowe opory przepływu:
![]()
długość całkowita rur o średnicy ½” Δl1=4,13m, a o średnicy ¾” Δl2=1,025m, więc:
dla rur o średnicy ½”:
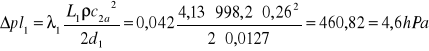
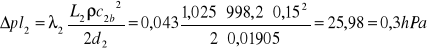
, czyli łącznie:
![]()
Liczba Reynoldsa zmienia się w zależności od średnicy rurki, toteż w rurce o średnicy ¾” jest ona większa, jednak nie zmienia to charakteru przepływu, który pozostaje burzliwy.
Wyznaczenie oporów miejscowych.
Zmiana przekroju i kierunku przepływu powoduje zawirowania strumienia, co z kolei generuje straty energii płynu, a w efekcie straty ciśnienie. Opory te nazywa się oporami miejscowymi, które opisuje wzór:
![]()
gdzie:
ρ - gęstość cieczy
c - średnia prędkość przepływu
ξ - Współczynnik oporów miejscowych
Wartość ξ zależy tylko od kształtu elementów na których występują zawirowania
Z tablicy 6 odczytano współczynniki oporów miejscowych ξ dla kolejnych elementów:
ξ1 = 0,5, ξ 2 = 1,1, ξ 3 = 1,1, ξ 4 = 1,1, ξ 5 = 0,118, ξ 6 = 0,22, ξ 7 = 0,14, ξ 8 = 1,1, ξ 9 = 1,1, ξ 10 = 1
Σ ξ = ξ1 + ξ 2 + ξ 3 + ξ 4 + ξ 5 + ξ 6 + ξ 7 + ξ 8 + ξ 9 + ξ 10
Σ ξ = 7,478
Wartości współczynników miejscowych oporów odczytane zostały z tablicy 6.
Ciecz przepływając przez kanał o zmiennym przekroju oraz zmiennym kierunku przepływu (kolanka lub rozdzielacze), pokonuje również miejscowe opory przepływu:
na wlocie przewodu ξ1 = 0,5
![]()
,
na pierwszym kolanku, ξ 2 = 1,1
![]()
na drugim kolanku, ξ 3 = 1,1
![]()
na trzecim kolanku, ξ 4 = 1,1
![]()
na nagłym rozszerzeniu, ξ 5 = 0,118, ponieważ:
![]()
, stąd przy wykorzystaniu interpolacji liniowej wyznaczono ξ5:
![]()
, czyli:
![]()
na nagłym zwężeniu ξ 6 = 0,22, ponieważ:
![]()
, czyli
![]()
![]()
Na łagodnym kolanku, ξ 7 = 0,14
, ponieważ promień zaokrąglenia R > 3d
![]()
na czwartym kolanku, ξ 8 = 1,1
![]()
na piątym kolanku, ξ 9 = 1,1
![]()
na szóstym kolanku, ξ 10 = 1,1
![]()
na wylocie, ξ 11 = 1
![]()
,
Sumaryczny spadek ciśnienia podczas przepływu przez kanał wyraża się wzorem:
![]()
,
Δpm = 2,81 hPa.
Dla przepływu burzliwego przyjęto α=1 oraz g=10 m/s2, ρ=998,2 kg/m3
Wyznaczenie sumarycznych oporów przepływu.
Sumaryczne spadek ciśnienia wywołany oporami przepływu wyraża się wzorem:
![]()
![]()
Obliczenia dla drugiej serii pomiarowej.
Wyznaczenie oporów przepływów przy otwartych wszystkich zaworach.
Analogicznie do wcześniejszych obliczeń, wyznaczono średnią prędkość przepływu dla drugiej serii pomiarowej. Zmianie uległa prędkość przepływu, długość kanału o średnicy ½” oraz opory liniowe i miejscowe (spowodowane zamianą kolanka na trójnik) i odpowiednio wynoszą:
![]()
C2a=0,33 m/s
C2b-0,15 m/s
Δl1=6,295m,
ponieważ wydłużono kanał o następujące odcinki:l9= 1,495m oraz l10= 0,67m.
Charakter przepływu jest ciągle burzliwy, ponieważ w stosunku do pierwszej serii pomiarowej zwiększa się średnia prędkość przepływu, czyli zwiększa się też liczba Reynoldsa.
![]()
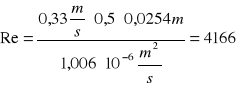
Re = 4166
A dla przepływu przez rurkę szerszą:
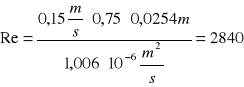
Re = 2840
Następnie wyznaczono empiryczny współczynnik liniowych oporów przepływu z tablicy 5
![]()
,
Gdzie współczynniki a, b, n przyjęto z równania Blassiusa:
a=0, b=0,3164, n=0,25
Po podstawieniu do wzoru otrzymano wartość współczynnika λ dla wąskiej rurki:
![]()
oraz dla szerokiej:
![]()
Dla przepływu burzliwego przyjęto ponownie α=1 oraz g=10 m/s2, ρ=998,2 kg/m3
Ponownie wyznaczono opory liniowe:
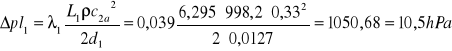
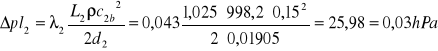
, czyli łącznie:
![]()
Wyznaczenie oporów miejscowych:
na wlocie przewodu ξ1 = 0,5
![]()
,
na pierwszym kolanku, ξ 2 = 1,1
![]()
na drugim kolanku, ξ 3 = 1,1
![]()
na trzecim kolanku, ξ 4 = 1,1
![]()
na nagłym rozszerzeniu, ξ 5 = 0,118, ponieważ:
![]()
, stąd przy wykorzystaniu interpolacji liniowej wyznaczono ξ5:
![]()
, czyli:
![]()
na nagłym zwężeniu ξ 6 = 0,22, ponieważ:
![]()
, czyli
![]()
![]()
Na łagodnym kolanku, ξ 7 = 0,14
, ponieważ promień zaokrąglenia R > 3d
![]()
na trójniku ξ 8 = 2
![]()
na piątym kolanku (są teraz dwa symetrycznie rozmieszczone), ξ 9 = 1,1
lecz po trójniku ciecz wypływa dwoma kanałami z dwiema prędkościami przepływu
c2a lewy=0,248 m/s = 0,25 m/s
c2a lewy=0,088m/s = 0,09 m/s
![]()
![]()
![]()
na szóstym kolanku (są teraz dwa symetrycznie rozmieszczone),, ξ 10 = 1,1
![]()
![]()
![]()
na wylocie (są teraz dwa symetrycznie rozmieszczone), ξ 11 = 1
![]()
![]()
![]()
Sumaryczny spadek ciśnienia podczas przepływu przez kanał wyraża się wzorem:
![]()
,
Δpm = 4,29 hPa.
Sumaryczny spadek ciśnienia wywołany oporami przepływu wyraża się wzorem:
![]()
![]()
Procentowy wzrost spadku ciśnienia wynosi zatem:
![]()
Δ(Δp)![]()
Wnioski.
Przepływ cieczy nieściśliwej przez różne przekroje oraz załamania w postaci kolanek i rozdzielaczy może powodować zmianę prędkości przepływu a nawet charakteru przepływu z burzliwego na laminarny i odwrotnie. Lepkość cieczy powoduje tarcie o ścianki przewodu, co znacząco wpływa na sposób przemieszczania się cieczy i rozkład jej prędkości. Zwiększenie chropowatości powierzchni rurki wydatnie zmniejsza prędkość przepływu przy ściankach (Rys. 4).
Rys. 9. Rozkład prędkości cieczy w rurce.
Przy dużej lepkości i bardzo nierównomiernym kanale przepływowym opory ruchu mogą być duże, że znacząco wpływają na obciążenie pompy tłoczącej czynnik. Spadek ciśnienia w kanale jest uzależniony od jego długości, średnicy i chropowatości zastosowanych powierzchni wewnętrznych rurek, charakteru załamań i zmian przekroju kanału oraz rodzaju zastosowanej cieczy. Jak pokazało doświadczenie, zwiększenie długości kanału zbudowanego z rurek o średnicy ½” o ok. 34% i zastosowanie trójnika spowodowało wzrost spadku ciśnienia o 48%.
W doświadczeniach zastosowano niedokładne przyrządy pomiarowe - pojemnik z niewystarczającą rozdzielczością podziałki oraz pomiar czasu przepływu przy wykorzystaniu stopera, co uniemożliwia idealną koordynację jego startowania i zatrzymywania wraz z rozpoczęciem i zakończeniem przepływu cieczy. Nie można zakładać, że zamknięcie zaworów wylotowych w drugiej serii pomiarowej zostało idealnie skoordynowane. W rzeczywistości jest bardzo prawdopodobne, że zawory nie zostały całkowicie otwarte lub zamknięte. Zakłócenia w przepływie mogły zostać także spowodowane zanieczyszczeniami czynnika roboczego, ponieważ w układnie nie zastosowano dokładnego systemu filtracji (zamontowano tylko siatkę o duże średnicy oczek)
Wszystkie powyższe czynniki wpływają niekorzystnie na jakość odczytów z serii pomiarowych, co z kolei uniemożliwiło wyznaczenie spadków ciśnienia z wysoką dokładnością.
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 148.
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 215.
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196..
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196.
Kaleta A., Górnicki K. „Materiały do wybranych ćwiczeń z techniki cieplnej”, str. 196..
Wyszukiwarka
Podobne podstrony:
ściąga TC, SGGW Technika Rolnicza i Leśna, Technika cieplna
sprawozdanie 1TC, SGGW Technika Rolnicza i Leśna, Technika cieplna
nasze tc 2, SGGW Technika Rolnicza i Leśna, Technika cieplna
sprawozdanie 2TC, SGGW Technika Rolnicza i Leśna, Technika cieplna
Sprawozdanie 3 dobre, SGGW Technika Rolnicza i Leśna, Technika cieplna
Sprawozdanie Grupa 4, SGGW Technika Rolnicza i Leśna, MS
sprawozdanie z wilgotności, studia, technika cieplna
sprawozdanie z ciśnień, studia, technika cieplna
sprawozdanie z wilgotności, studia, technika cieplna
sprawozdanie 3(1), SGGW Technika Rolnicza i Leśna, Technika cieplna
REGULATOR PID, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
IDENTYFIKACJA OBIEKTU, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
DOBÓR NASTAW REGULATORÓW W MODELOWYM UKŁADZIE AUTOMATYCZNEJ REGULACJI, SGGW Technika Rolnicza i Leśn
Wzor sprawozdania, SGGW Technika Rolnicza i Leśna, Automatyka
Sprawozdanie Automatyka systemy liczbowe, SGGW Technika Rolnicza i Leśna, Automatyka
BADANIE PRZETWORNIKÓW, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
SKALOWANIE PRZYRZĄDU APARATURY DO POMIARU DŁUGOŚCI, SGGW Technika Rolnicza i Leśna, Automatyka, Spra
sciaga cieplo!, SGGW Technika Rolnicza i Leśna, Technika cieplna
więcej podobnych podstron