6.2 Dipol elektryczny

Obliczenie pola elektrycznego

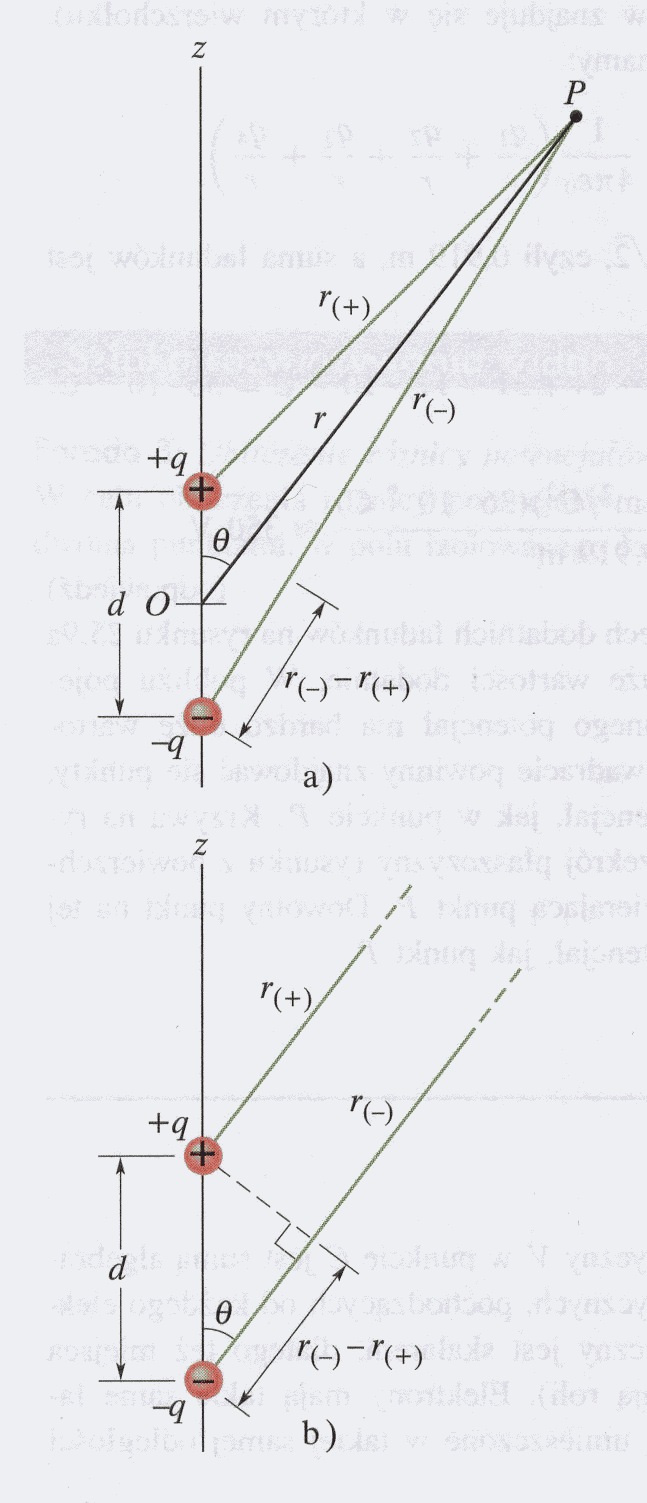
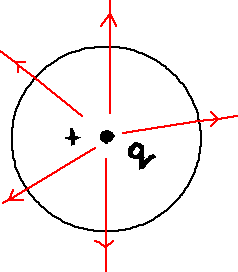
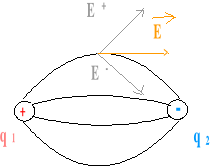
Dipol elektryczny składa się z dwóch równych co do wartości ładunków przeciwnego znaku oddalonych od siebie o odległość równą 2a. Obliczmy pole elektryczne w dowolnej odległości r leżącej na symetralnej prostopadłej do osi dipola. Ponieważ
stąd
, stąd wypadkowe pole jest sumą wektorową

gdzie: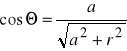
i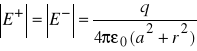

stąd pole wynosi

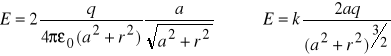
przyjmując, że moment dipolowy p=2aq

stąd
, jeśli (r>>a).

Obliczenie potencjału

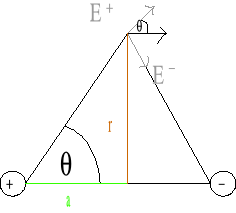
Rozpatrzmy punkt P odległy o r od środka osi dipola. Ponieważ potencjał wypadkowy jest sumą potencjałów od poszczególnych ładunków stąd:

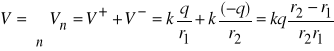
, jeżeli r>>l to możemy przyjąć, że
oraz

Ostatecznie
, gdzie
jest momentem dipolowym.

Pytania:

1. Wykaż, że wartość E w punkcie P leżącym na osi kwadrupola w odległości r od jego środka (przy założeniu r>>a) jest dana wzorem

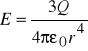
gdzie
jest momentem kwadrupolowym takiego rozkładu ładunków

Rys

2. Wylicz wypadkowy potencjał V(r) w punkcie P od takiego kwadrupola jak na rysunku..

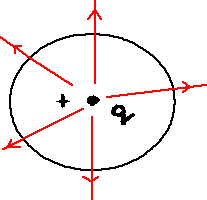
6.3 Przykłady zastosowania prawa Gaussa

Obliczenie pola elektrycznego ładunku punktowego

Przyjęto kulisty kształt powierzchni Gaussa

skąd pole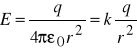
; siła Coulomba

Liniowy rozkład ładunków

Jednorodnie naładowany nieskończenie długi (l>>r) cienki pręt (drut)

gęstość liniowa

zał.
wybieramy powierzchnię Gaussa w kształcie walca

Z prawa Gaussa

Ostatecznie pole wynosi:

Pytanie

Wykonaj obliczenia pola elektrycznego i potencjału dla:

1. pręta z izolatora o promieniu R naładowanego ładunkiem dodatnim jednorodnie w całej objętości,

2. dla naładowanego dodatnio pręta metalowego o promieniu R.

Rozważ przypadki: R>r i R<r. Wskazówka: przeanalizuj co się dzieje z ładunkiem dodatnim wprowadzanym do metalu.

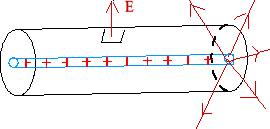
Płaski rozkład ładunków

Nieskończona naładowana płaszczyzna

gęstość powierzchniowa

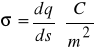
zał. płaszczyzna naładowana jest jednorodnie cz.

Przyjmując powierzchnię Gaussa w kształcie walca o podstawie S wyliczamy

całkowity strumień
z prawa Gaussa
stąd

po uwzględnieniu gęstości powierzchniowej pole wynosi:

Pole zależy od gęstości ładunku, nie zależy od odległości.

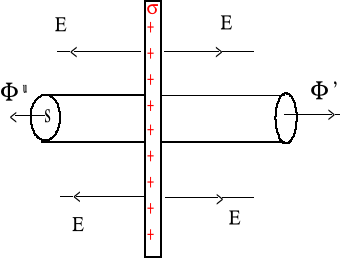
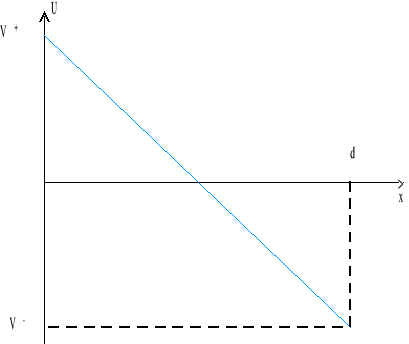
Dwie nieskończone płaszczyzny naładowane różnoimiennie

zał. płaszczyzny naładowane są jednorodnie cz.
i oddalone są o d (0 ≤ x ≤ d).

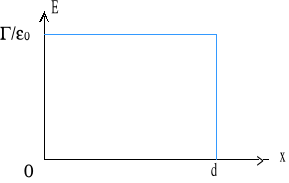
Pole elektryczne pomiędzy płaszczyznami (wewnątrz płaskiego kondensatora) jest stałe i wynosi:

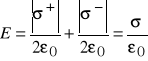
na zewnątrz pole E = 0.

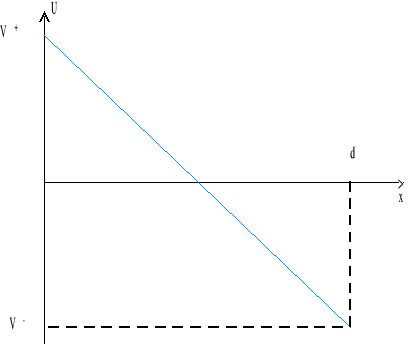
Obliczenie różnicy potencjałów

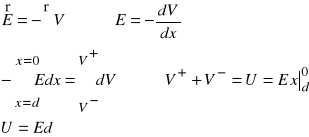
Powierzchnia przewodnika

Na powierzchni metalicznej (przewodzącej) cały ładunek gromadzi się na zewnątrz (wewnątrz pole E=0), istnieje tylko składowa prostopadła do powierzchni a składowa styczna równa się zeru (gdyby istniała składowa styczna to płynąłby po powierzchni prąd wywołany ruchem elektronów).

Linie sił pola wychodzą na zewnątrz powierzchni (przechodzą tylko przez jedną podstawę S powierzchni Gaussa w kształcie walca).

Rozkład objętościowy ładunków

Izolowany przewodnik

Jeśli na metaliczny, objętościowy przewodnik izolowany (aby nie odprowadzał ładunków) wprowadzimy, w sposób przypadkowy, ładunek to będzie on wytwarzał pole elektryczne przemieszczające swobodne elektrony ku powierzchni przewodnika, aż do momentu kiedy pole wewnątrz zniknie. Zastosujmy twierdzenie Gaussa dla przewodnika o dowolnym kształcie z zamkniętą powierzchnią Gaussa tuż poniżej powierzchni przewodnika.

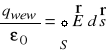
ponieważ pole E = 0 wewnątrz to q_wew = 0, czyli nie istnieje ładunek wewnątrz, ponieważ cały ładunek zgromadził się na powierzchni przewodnika.

Pytania

Posługując się analogią z pola grawitacyjnego rozwiąż następujące zadania:

1. Jednorodnie naładowana sfera kulista o promieniu R

1. wylicz pole elektryczne w odległości R ≥ r i r ≥ R

2. wylicz potencjał w odległości R ≥ r i r ≥ R.

2. Te same obliczenia przeprowadź dla pełnej metalowej kuli o promieniu R.

3. Jednorodnie naładowana w całej objętości kula (z izolatora) o promieniu R

1. wylicz pole elektryczne w odległości R ≥ r i r ≥ R

2. 
   wylicz potencjał w odległości R ≥ r i r ≥ R.

Energia pola elektrycznego.

Pojemność

Energia ładowania = energii rozładowania kondensatora

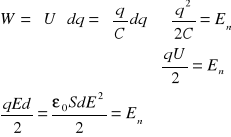
Objętość kondensatora V_obj= S d

Gęstość energii ⇒

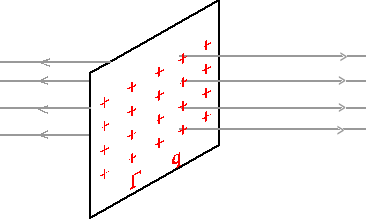
6.4. Dielektryki, prawo Gaussa dla dielektryków.

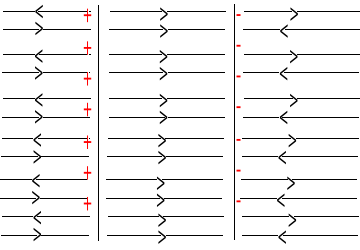
Dielektryki - ładunki nie mogą się swobodnie przemieszczać ale możliwe są przesunięcia ładunków w skali mikroskopowej.

q - ładunek swobodny

q' - ładunek polaryzacyjny

- bez dielektryka

- z dielektrykiem

q - q' = ε₀E⋅S

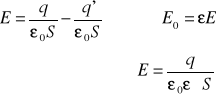
Wektor polaryzacji:
zwrot wektora: od ładunku ujemnego do dodatniego ładunku indukowanego - jak w każdym dipolu.

Gdzie
= q'⋅ d jest to moment dipolowy ⇒
moment dipolowy jednostki objętości

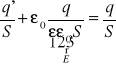
A więc

- wektor indukcji

- łączy ładunki polaryzacyjne

- dotyczy wszystkich ładunków

- łączy ładunki swobodne (jest taki sam dla próżni i dielektryka)

Podatność dielektryczna:
gdzie A - stała Curie-Weissa.

E=0 E E=0

σ/ε₀

- -

- - S

- -

- -

ii

+ +

+ + + + + +

d

- - - - - - - - - - - -

+ + + + + + + + +

+ + + + + + + + + + + +

- - - - - - - - - - - - - - -

q

q'

+q

- q'

+q'

-q

- - - - - - - - - - - -

+ + + + + + + + +

+ + + + + + + + + + + +

- - - - - - - - - - - - - - -

D

P

ε₀E

D ε₀E

E

D

T_C

T

P_S

ferro-

-para elektryk

χ

T_C

T

---