Cyfrowe układy logiczne

Układy cyfrowe (ang. digital circuits) to układy elektroniczne, które przetwarzają s) ły napięciowe o różnych poziomach. Zazwyczaj są to dwa poziomy: wysoki (ang. lub niski (ang. Iow), którym przypisane są wartości binarne 1 (wysoki) oraz 0 (nisl

Układy cyfrowe przetwarzające informacje w systemie binarnym realizują ope zgodnie z algebrą BooleV, dlatego nazywane są również układami logicznymi i logie circuits) lub przełączającymi. Cyfrowe układy logiczne (ang. digital logie circ wykonują operacje logiczne typu suma logiczna (OR), iloczyn logiczny (AND) negacja (NOT) według aksjomatów² boole'owskich i reprezentowane są przez bn logiczne (rysunek 4.1).

Rysunek 4.1.

Reprezentacja bramek OR i AND z wykorzystaniem przełączników, baterii i żarówki

Współczesne układy logiczne budowane są najczęściej jako układy scalone (ang.;'; grated circuits), dzięki czemu projektowane systemy mogą mieć niewielkie rozmiar

W niniejszym rozdziale omówione zostanie pojęcie informacji cyfrowej oraz ta zagadnienia, jak funktory logiczne, układy logiczne, przerzutniki, liczniki, sumatc rejestry i pamięci.

¹ George Boole, dziewiętnastowieczny angielski matematyk, samouk.

² Twierdzenie, które przyjmuje się za pewnik bez dowodu.

4.1. Informacja cyfrowa

Informacja cyfrowa (ang. digital information) to informacja zakodowana w postaci ciągów liczb binarnych składających się ze słów binarnych 0 i 1.

4.1.1. Podstawowe jednostki informacji

Podstawową umowną jednostką informacji cyfrowej jest bit (binary digit — cyfra dwójkowa), który przyjmuje dwie wartości: 1 lub 0. Fizycznie układy cyfrowe realizują bity za pomocą dwóch stanów, zwykle za pomocą dwóch różnych napięć.

W uproszczonym modelu można założyć, że w układzie cyfrowym 0 (stan niski, Iow) Reprezentowane jest przez napięcie bliskie 0 V, natomiast 1 (stan wysoki, high) — przez napięcie znacznie wyższe, na przykład około 5 V (rysunek 4.2). Ciąg kolejnych stanów niskich i wysokich nazywa się sygnałem cyfrowym (ang. digital signal).

11—. ^

Rysunek 4.2. Fizyczna reprezentacja zer i jedynek (sygnał cyfrowy)

Niektóre urządzenia techniki komputerowej nie operują na pojedynczych bitach —

posługują się grupami bitów, tzw. bajtami (ang. byte), które zawierają najczęściej 8

litów. Przykładami urządzeń operujących bajtami są pamięci operacyjne, pamięci ma-

sowe, drukarki.

4.1.2. Mnożniki binarne

W życiu codziennym często spotykamy się z mnożnikami dziesiętnymi typu kilogram, kilometr, megatona, stosowanymi w celu skrócenia zapisu liczb dziesiętnych. Wygod-niej przecież zapisać wartość 1000 g (gram) w postaci 1 kg (kilogram).

Rozwój informatyki pozwala urządzeniom techniki komputerowej na przetwarzanie coraz większej ilości danych. Posługiwanie się podstawowymi jednostkami, czyli bi-tem i bajtem, może być nieefektywne i nieatrakcyjne wizualnie, dlatego również w sys-temie binarnym stosowane są tzw. mnożniki binarne (ang. binary multiples).

Istnieją różnice w określaniu wartości i zapisie mnożników dziesiętnych i dwójko­wych (binarnych). W systemie dziesiętnym podstawą jest liczba 10, więc poszcze-

ROZDZIAŁ 4 ■ Cyfrowe uktady logiczne

gólne mnożniki stanowią wielokrotność dziesiątki. Na przykład 1000 gramów jest odpowiednikiem 10³ (1 kilo-gram), a 1 000 000 ton to 10⁶ (1 mega-tona). W syste­mie dwójkowym podstawą jest liczba 2, więc 1 kilogram to 2¹⁰, czyli 1024, a nie jak w przypadku mnożników dziesiętnych — 1000. Oznaczenia wielokrotności dziesięt­nych zawiera tabela 4.1.

Tabela 4.1. Oznaczenia wielokrotności dziesiętnych

Wielokrotność	Symbol	Nazwa	Wartość
10^3	k*	Kilo	1000
10^6	M	Mega	1 000 000
10^9	G	Giga	1 000 000 000
10^12	T	Tera	1 000 000 000 000
10^15	P	Peta	1 000 000 000 000 000
10^18	E .	Eksa	1 000 000 000 000 000 000
10^2ł	Z	Zeta	1 000 000 000 000 000 000 000

* Symbol „k" dla Kilo jest pisany małą literą (dla zapewnienia zgodności ze standardem SI)

W 1998 r. w celu uniknięcia nieporozumień związanych z mnożnikami binarnymi komisja IEC (ang. International Electrotechnical Commission — międzynarodowa ko­misja elektrotechniczna) opracowała międzynarodowy standard nazw symboli wielo­krotności binarnych (tabela 4.2).

Tabela 4.2. Oznaczenia wielokrotności binarnych

Wielo- Pochodzenie Symbol Nazwa Wartość

krotność

1024

1 048 576

1 073 741 824

1099 511627 776

1 125 899 906 842 624

1 152 921 504 606 846 976

1 180 591 620 717 411 303 424

1 208 925 819 614 629 174 706 176

Problemem jest to, że niewiele osób stosuje standard IEC i wciąż widzimy ozna­czenia 1024 Kb, 1024 KB, mimo że dotyczą wielokrotności binarnych — powinno stosować się zapis 1024 Kib, 1024 MiB itd. (tabela 4.3).

Tabela 4.3. Porównanie oznaczeń wielokrotności dziesiętnych i binarnych

dla bitów i bajtów

	Wielokrotności dziesiętne		Wielokrotności binarne
Bit	Bajt	Bit	Bajt
1b	1B	1b	1B
l kb	lkB	lKib	lKiB
1Mb	1MB	1Mib	IMiB
1Gb	1GB	1 Gib	1 GiB
1Tb	1TB	lTib	lTiB
IPb	IPB	lPib	1 PiB

4.2. Algebra Boole'a

Fundamentem współczesnej logiki matematycznej oraz techniki cyfrowej jest zbiór aksjomatów opracowanych przez angielskiego matematyka George'a Boole'a, które przedstawił w dziele An Investigation of the Lows of Touch (O prawach logicznego .wnioskowania).

Algebrą Boole'a nazywa się niepusty zbiór A, w którym znajdują się dwa elementy 0,1 oraz określone są dwuargumentowe działania sumy (+ lub v) i iloczynu (* lub a) oraz jedno działanie jednoargumentowe nazywane dopełnieniem lub negacją (- lub ­), spełniające następujący układ aksjomatów (dla a, b, c <= A):

1. avb = bva; a^b = b^a — przemienność

2. av(bvc) = (avb)vc; a^(b^Ć) - {a^b)^c— łączność.

3. av{b^c) = (avb)^(avc); a^(bvc) = (a^b)v(a^c) — rozdzielność.

4. av(a^b) = a; a^(avb) = a — absorpcja.

5. av0 = a; a^1 = 1 — identyczność

6. Dla dowolnego elementu a e A istnieje -a e A taki, że: av-a = 1; a^-a = 0 — dopełnienie.

4.3. Funktory logiczne

Funktory logiczne (ang. logical functors) potocznie nazywane bramkami logicznymi

(ang. logie gates) są elementami konstrukcyjnymi układów cyfrowych, składającymi się z odpowiednio połączonych rezystorów, tranzystorów, kondensatorów i diod pół­przewodnikowych (rysunek 4.3).

Rysunek 4.3.

Schemat budowy bramki NAND LS-TTL

Funktory logiczne przedstawiane są graficznie za pomocą piktogramów (symboli gra­ficznych), dzięki czemu istnieje możliwość projektowania systemów logicznych na pa­pierze lub za pomocą oprogramowania komputerowego. Podstawowe bramki logicz­ne AND, OR i NOT odzwierciedlają funkcje logiczne opisane przez algebrę Boole'a. Współcześnie fizyczne funktory rzadko buduje się na bazie pojedynczych elementów półprzewodnikowych, najczęściej korzysta się z gotowych bramek zawartych w ukła­dach scalonych typu TTL lub CMOS (rysunek 4.4).

Rysunek 4.4.

Schemat układu scalonego TTL7409 zawierającego 4 bramki AND

Podstawowe bramki OR i AND (oraz pochodne) mają dwa wejścia i jedno wyjście, natomiast bramka NOT ma jedno wejście i jedno wyjście. Działanie funktorów pre­zentowane jest za pomocą tablic prawdy, w których opisuje się kolejne kombinacje stanów na wejściach oraz odpowiednie wartości na wyjściu.

4.3.1. Bramka OR

Bramka OR (LUB) (rysunek 4.5) realizuje sumę logiczną Y = A+B lub Y = AvB.

A \ -^ Rysunek 4.5.

Symbol bramki OR

Działanie funktora OR opisuje tablica prawdy:

A	B	Y
1	1	1
1	0	1
0	1	1
0	0	0

Funktor OR daje na wyjściu Y stan 1 wtedy, gdy przynajmniej na jednym wejściu będzie również stan 1. Stan 0 na wyjściu Y pojawi się tylko wtedy, gdy na wejściach A i B pojawi się stan 0.

UWAGA

Istnieją również bramki OR mające kilka wejść, na przykład A, B, C, D, które opisuje funkcja Y = A+B+C+D.

4.3.2. Bramka AND

Bramka AND (i) (rysunek 4.6) realizuje iloczyn logiczny Y = A*B lub Y = A^B.

Rysunek 4.6.

Symbol bramki AND

Działanie funktora AND opisuje tablica prawdy:

A	B	Y
1	1	1
1	0	0
0	1	0
0	0	0

Bramka AND daje na wyjściu Y stan 0 wtedy, gdy przynajmniej na jednym wejściu będzie również stan 0. Stan 1 na wyjściu Y pojawi się tylko wtedy, gdy na wejściu A i B pojawi się stan 1.

UWAGA

Istnieją również bramki AND mające kilka wejść, na przykład A, B, C, które opisuje funkcja Y = A*B*C.

4.3.3. Bramka NOT

Bramka NOT (NIE) (rysunek 4.7) realizuje negację Y = A .

Rysunek 4.7.

Symbol bramki NOT

Działanie funktora NOT opisuje tablica prawdy:

A Y

0 1

1 0

Funktor NOT daje na wyjściu Y stan 1 tylko wtedy, gdy na wejściu będzie stan 0. Stan 0 na wyjściu Y pojawi się tylko wtedy, gdy na wejściu A pojawi się stan 1.

Bramka NOT wykonuje inwersję, zamieniając 1 na 0 i odwrotnie.

4.3.4. Bramka NOR

Bramka NOR, NOT-OR (NIE-LUB) (rysunek 4.8) realizuje sumę logiczną z inwersją Y = a+B lub Y = AvB .

Rysunek 4.8.

Symbol bramki NOR

Działanie funktora NOR opisuje tablica prawdy:

A	B	Y
1	1	0
1	0	0
0	1	0
0	0	1

Bramka NOR wykonuje operacje odwrotnie niż bramka OR Funktor NOR daje na wyjściu Y stan 0 wtedy, gdy przynajmniej na jednym wejściu będzie stan 1. Stan 1 na wyjściu Y pojawi się tylko wtedy, gdy na wejściach A i B będzie stan 1.

UWAGA

Istnieją również bramki NOR mające kilka wejść, na przykład A, B, C, D, które opisuje

funkcja Y = A + B + C + D

4.3.5. Bramka NAND

Bramka NAND, NOT-AND (NIE-I) (rysunek 4.9) realizuje iloczyn logiczny z inwersją

Y=A*B lub Y = A^B . A

Rysunek 4.9.

Symbol bramki NAND

Działanie funktora NAND opisuje tablica prawdy:

A	B	Y
1	1	0
1	0	1
0	1	1
0	0	1

Funktor NAND wykonuje operacje odwrotnie niż AND. Bramka NAND daje na wyj­ściu Y stan 1 wtedy, gdy przynajmniej na jednym wejściu będzie również stan 1. Stan 0 na wyjściu Y pojawi się tylko wtedy, gdy na wejściu A i B pojawi się stan 1.

UWAGA

Istnieją również bramki NAND mające kilka wejść, na przykład A, B, C, które opisuje funkcja Y = A*B*C .

4.3.6. Bramka XOR, EX-OR

Bramka XOR, EXCLUSIVE-OR (ALBO) (rysunek 4.10) realizuje różnicę symetryczną (sumę poprzeczną) Y = A* B + A*B lub Y=A^BvA^B lub Y = A® B .

Rysunek 4.10.

Symbol bramki XOR

ROZDZIAŁ 4 ■ Cyfrowe układy logiczne

Działanie funktora XOR opisuje tablica prawdy:

A. .	B	Y
1	1	0
1	0	1
0	1	1
0	0	0

Bramka XOR daje na wyjściu Y stan 1 wtedy, gdy przynajmniej na jednym wejściu będzie również stan 1. Stan 0 na wyjściu Y pojawi się tylko wtedy, gdy na obydwu wejściach A i B pojawi się stan 1 lub 0.

4.3.7. Półsumator

Funktory logiczne wykonują operacje logiczne. Aby stworzyć układ cyfrowy wykonu­jący operacje arytmetyczne, należy go zaprojektować z wykorzystaniem odpowiednio połączonych bramek.

Prostym układem sumującym liczby binarne jest półsumator (rysunek 4.11). Układ półsumatora ma dwa wejścia A i B., na które podaje się sumowane bity, oraz dwa wyjścia. Na wyjściu Wi sumator zwraca wyniki sumowania, na wyjściu C — bity przeniesienia.

Półsumator zbudowany jest z bramki XOR i AND, gdzie XOR generuje wyniki, a funk-tor AND odpowiedzialny jest za bity przeniesienia (rysunek 4.12). Wyjście W realizuje różnicę symetryczną W = A*B + A*B, natomiast przeniesienie realizowane jest przez iloczyn C = A*B.

Rysunek 4.12.

Schemat logiczny półsumatora

4.4. Układy cyfrowe

Działanie półsumatora przedstawia tablica prawdy:

4.4. Układy cyfrowe

Funktory logiczne umożliwiają projektowanie układów cyfrowych (ang. digital circu-its), które pozwalają realizować zadania logiczne i arytmetyczne.

Fizycznie układy cyfrowe mogą być budowane za pomocą półprzewodnikowych ele­mentów elektronicznych, takich jak rezystory, tranzystory, diody, kondensatory. Takie układy zazwyczaj charakteryzują się dużymi rozmiarami, sporym poborem mocy oraz małą sprawnością i wydajnością. Dlatego współczesne układy cyfrowe mają najczę­ściej postać elektronicznych układów scalonych (ang. integrated circuits).

Układy cyfrowe można podzielić ze względu na różne kryteria, na przykład sposób przetwarzania informacji, technologię wykonania.

ROZDZIAŁ 4 ■ Cyfrowe układy logiczne

4.4.1. Układy sekwencyjne i kombinacyjne

Ze względu na sposób przetwarzania informacji wyróżniamy dwie grupy układów cyfrowych: sekwencyjne oraz kombinacyjne.

W układach sekwencyjnych (ang. seauential circuits) wynik na wyjściu zależy od stanu na wejściu oraz stanu poprzedniego. Stan poprzedni nazywany jest stanem wewnętrznym i przechowywany jest w wewnętrznej pamięci układu zwanej rejestrem (rysunek 4.14).

Rysunek 4.14.

Działanie układu sekwencyjnego

Istnieją dwie odmiany układów sekwencyjnych: asynchroniczne i synchroniczne. W układach asynchronicznych zmiana stanu na wejściu X powoduje natychmiastową zmianę na wyjściu Y. Układy takie są szybkie, ale jednocześnie podatne na zakłócenia. W układach synchronicznych zmiana sygnału wejściowego zależy od dodatkowego sygnału zegarowego CLK (ang. clock). Mimo braku zmiany stanu wejściowego może tu następować zmiana stanu wewnętrznego.

Układy kombinacyjne (ang. combinational circuits) charakteryzują się tym, że ich stan wyjściowy zależy wyłącznie od stanu na wejściu.

4.4.2. Układy bipolarne i unipolarne

Układy cyfrowe można podzielić również ze względu na technologię wytwarzania tranzystorów, z których budowane są funktory logiczne. Wyróżnić można układy cy­frowe bipolarne i unipolarne (więcej na ten temat w rozdziale 6.).

Układy bipolarne (ang. bipolar circuits) TTL (ang. Transistor-Transistor Logic) to jedna z najstarszych odmian układów scalonych zbudowanych z wykorzystaniem tranzy­storów bipolarnych. Popularność zdobyły układy z rodziny SN74xx produkowane do dnia dzisiejszego. Napięcie zasilania wynosi 5 V±5%, stan niski od 0,2 do 0,8 V, a wy­soki od 2 do 5 V. Układy TTL pobierają w stanie statycznym ze źródła zasilania dość dużo prądu, a im szybszy układ, tym pobór mocy jest większy.

Układy unipolarne (ang. unipolar circuits) CMOS (ang. Complementary MOS) bu­dowane są na bazie tranzystorów polowych MOS (ang. Metal-Oxide Semiconductor), dzięki czemu charakteryzują się małym poborem mocy. Układy CMOS mogą być zasi­lane znacznie szerszym zakresem napięć niż TTL, w zależności od wersji może to być od 2 do 6 V (HC) lub od 3 do 15 V (AC). Stan niski wynosi 0 V, stan wysoki jest równy napięciu zasilania (VDD). Układy rodziny CMOS nie pobierają w ogóle prądu w stanie statycznym. Niemniej moc zasilania rośnie w nich liniowo wraz ze wzrostem częstotli­wości. Układy CMOS pracujące blisko górnej dopuszczalnej częstotliwości pobierają ze źródła zasilania niemal tyle samo mocy, co układy TTL. Większość układów z prze­znaczeniem dla komputerów jest budowana w technologii CMOS.

4.4.3. Symbole wybranych elementów elektronicznych

ROZDZIAŁ 4 ■ Cyfrowe układy logiczne

4.5. Układy scalone

Układ scalony (ang. integrated circuit) to zminiaturyzowany układ elektroniczny za­wierający w swoim wnętrzu od kilku do setek milionów podstawowych elementów elektronicznych, takich jak tranzystory, diody, rezystory, kondensatory, połączonych w funkcjonalną całość

Fizycznie układ scalony przyjmuje najczęściej postać monokrystalicznej kwarcowej płytki umieszczanej w hermetycznej obudowie z metalu, plastiku lub ceramiki (rysu­nek 4.15). Układ tworzony jest podczas wieloetapowego procesu technologicznego nazywanego technologią planarną.

Rysunek 4.15. Układy scalone w różnego typu obudowach

Układy o dużym stopniu scalenia osadzane są najczęściej w obudowach tupu DIP (ang. Dual In-line Package), o liczbie wyprowadzeń od 4 do 48. Drugą popularną grupę stanowią obudowy TO, w których umieszczane są niektóre układy scalone, tranzysto­ry, wzmacniacze czy stabilizatory.

Nóżki układów scalonych są odpowiednio numerowane (rysunek 4.4), od 1 do ostatnie­go wyprowadzenia na przykład od 1 do 14. Z jednej strony układu znajduje się wcięcie lub kropka sygnalizująca lewą stronę układu, wtedy numeracja nóżek rozpoczyna się od lewego dolnego rogu i biegnie wokół układu scalonego. Wyprowadzenia zasilania w układach TTL oznaczone są jako V_cc, a w CMOS ■

V_DD. Masa ma oznaczenie GND.

Do głównych zalet układów scalonych można zaliczyć:

• dużą integrację elementów (miniaturyzacja),

• mały pobór mocy,

• dużą niezawodność,

• niską cenę,

• dużą częstotliwość pracy.

4.5.1. Układy analogowe, cyfrowe i mieszane

Scalone układy cyfrowe można sklasyfikować ze względu na rodzaje obsługiwanych sygnałów. Układy scalone mogą obsługiwać sygnały cyfrowe, analogowe i mieszane.

Scalone układy cyfrowe przystosowane są do przetwarzania sygnału cyfrowego w po­staci dwóch stanów: wysokiego (High — 1) oraz niskiego (Low — 0). Dwustanowy sygnał nazywany jest binarnym.

72

4.5. Układy scalone

Analogowe układy scalone przystosowane są do przetwarzania sygnałów w postaci napięć lub prądów, których wartości zmieniają się w sposób ciągły. Sygnał analogowy ma postać sinusoidy o zmiennej amplitudzie i natężeniu.

Układy mieszane potrafią przetwarzać sygnał cyfrowy i analogowy.

4.5.2. Układy monolityczne i hybrydowe

Kolejnym kryterium podziału układów scalonych jest sposób realizacji wewnętrznych elementów biernych i czynnych — w ramach tego rozróżnia się scalone układy mono­lityczne oraz hybrydowe.

W monolitycznych układach scalonych wszystkie elementy (czynne i bierne) wy­konane są w monokrystalicznej strukturze półprzewodnika (kwarcowa płytka) (ry­sunek 4.16). Większość współczesnych układów wytwarzana jest w technologii mo­nolitycznej.

Rysunek 4.16.

Monolityczna płytka kwarcowa zamontowana w obudowie

Układy hybrydowe wykonane są z izolatora z naniesionymi warstwami przewodnika i materiału rezystywnego. Warstwy te tworzą układ połączeń elektrycznych oraz rezy­story. Do tego rodzaju płytek dołącza się miniaturowe układy monolityczne (rysunek 4.17). Ze względu na grubość warstw rozróżnia się układy:

• cienkowarstwowe (warstwy około 2 mikrometrów)

• grubowarstwowe (warstwy od 5 do 50 mikrometrów).

Rysunek 4.17.

Płytka układu hybrydowego

73

4.5.3. Podział ze względu na stopień scalenia

Układy scalone są wytwarzane w różnych stopniach integracji (scalenia), co oznacza, że elementy układów mogą mieć różne rozmiary. Pomniejszone rozmiary elementów powodują, że na płytce o takiej samej powierzchni mieści się ich więcej.

Wyróżnia się następujące stopnie integracji:

• mała skala integracji (ang. Smali Scalę of Integration, SSI),

• średnia skala integracji (ang. Medium Scalę of Integration, MSI),

• duża skala integracji (ang. Large Scalę of Integration, LSI),

• wielka skala integracji (ang. Very Large Scalę of Integration, VLSI),

• ultrawielka skala integracji (ang. Ultra Large Scalę of Integration, ULSI).

4.5.4. Oznaczenia cyfrowych układów scalonych

System oznaczeń monolitycznych układów scalonych w Polsce reguluje norma BN-73/3375-21, która dzieli układy na dwie grupy: do użytku powszechnego oraz układy profesjonalne.

Oznaczenia układów składają się z części literowej (dwie lub trzy litery) oraz numeru seryjnego (kilka cyfr i litera). Część literowa zawiera informacje dotyczące rodzaju układu scalonego, przeznaczenia i sposobu wykonania. Numer seryjny zawiera infor­macje dotyczące wytrzymałości temperaturowej czy rodzaju obudowy.

Oznaczenia z części literowej:

I. Pierwsza litera:

M — monolityczny układ scalony zbudowany na bazie tranzystorów MOS.

U — monolityczny układ scalony zbudowany na bazie tranzystorów bipolarnych.

II. Druga litera:

C — układ scalony cyfrowy. L — układ scalony analogowy.

III. Trzecia litera:

A — zastosowania specjalne.

Y — przeznaczenie profesjonalne.

T — przeznaczenie profesjonalne o podwyższonej niezawodności.

Brak litery — do zastosowania powszechnego.

Oznaczenia cyfrowe:

Cyfra	Zakres temperatury
4	-55- +85°C
5	-55-+125°C
6	-40- +85°C
7	0- +70°C
8	-25- +85°C
1	Inny

Pozostałe trzy lub cztery cyfry są liczbami porządkowymi. Litera po grupie cyfr ozna­cza rodzaj obudowy:

F — płaska obudowa metalowa izolowana od układu.

S — płaska obudowa metalowa mająca kontakt elektryczny z układem oraz wy­prowadzeniem masy.

H — obudowa ceramiczna (z materiału nieprzewodzącego).

J — obudowa dwurzędowa ceramiczna (z materiału nieprzewodzącego).

N — obudowa plastikowa.

L — obudowa kubkowa o wyprowadzeniach umieszczonych kołowo.

R — inna obudowa.

4.6.. Przerzutniki

Przerzutnik (ang. flip-flop) jest najprostszym układem z pamięcią, który umożliwia zapamiętanie 1 bitu informacji. Z kilku przerzutników budowane są bardziej skompli­kowane układy cyfrowe, na przykład rejestry. Wyróżnia się kilka odmian przerzutni­ków: RS, JK, D, T, JK-MS.

Przerzutnik ma dwa stany wewnętrzne 1 i 0 reprezentowane przez wyjście przerzut-nika Q (przerzutniki mają również wyjście zanegowane). Zmiana stanu przerzutnika następuje pod wpływem zmiany wartości sygnałów wejściowych.

Ze względu na moment zmiany przerzutniki dzieli się na:

• asynchroniczne — pracują bez sygnału taktującego, a stan przerzutnika ustala się bezpośrednio w wyniku zmiany stanu wejść;

• synchroniczne — pracują z udziałem sygnału taktującego, a stan wejść infor­macyjnych jest przekazywany na wyjście w chwilach występowania określonego poziomu lub narastającego (opadającego) zbocza sygnału taktującego.

Na schematach można spotkać następujące oznaczenia sygnałów sterujących:

4.6.1. Przerzutnik RS

Przerzutnik RS (ang. Reset - Set) zbudowany może być z dwóch bramek NAND lub NOR (rysunek 4.18). Opiera swoje działanie na sprzężeniu zwrotnym (ang. feed back) wyjść z wejściami.

Rysunek 4.18.

Schemat przerzutników RS zbudowanych z dwóch bramek NAND

NOR

NAND

Przerzutnik RS (rysunek 4.19) oparty na bramkach NOR ma dwa wejścia: S (ang. Set — ustaw) i R (ang. Reset — zeruj) oraz dwa wyjścia: Q i Q. Działa według następują­cych zasad:

• S = 0iR = 0 — stan przerzutnika nie zmienia się;

• S = 0 i R = 1 — przerzutnik zostaje wyzerowany;

• S = 1 i R = 0 — następuje zmiana stanu przerzutnika;

• S = 1 i R = 1 — stan niedozwolony.

Rysunek 4.19.

Symbol przerzutnika RS

Przerzutnik synchroniczny RS ma dodatkowe wejście C, do którego doprowadza się sy­gnał taktujący (rysunek 4.20). Zmiana stanu przerzutnika synchronicznego następuje w chwilach wyznaczonych przez sygnał taktujący.

Rysunek 4.20.

Symbol synchronicznego przerzutnika RS

4.6.2. Przerzutnik JK

Przerzutnik JK jest klasycznym przykładem przerzutnika synchronicznego mającym dwa wejścia J i K oraz wyjścia Q i Q zanegowane (rysunek 4.21). Przerzutnik JK nie ma stanów wejściowych niedozwolonych. W przypadku jednoczesnego podania sy­gnałów 1 na wejścia J i K jego stan następny będzie negacją stanu aktualnego.

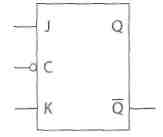
Rysunek 4.21.

— Symbol przerzutnika JK z zegarem reagującym na stan niski

Przerzutnik JK jest wersją przerzutnika RS rozbudowaną o dwie dodatkowe bramki NAND (rysunek 4.22).

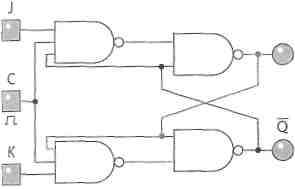
Rysunek 4.22.

q Budowa przerzutnika JK

Działanie przerzutnika JK opisuje tablica stanów:

Przerzutnik JK działa według następujących zasad:

• J = O i K = 0 — stan wejściowy nie wpływa na wyjściowy i przerzutnik pamięta stan wcześniejszy;

• J = 1 i K = 0 — na wyjściu pojawi się stan wysoki;

• J = 0iK=l — na wyjściu pojawi się stan niski;

• J = 1 i K = 1 — na C cyklicznie będzie się pojawiało 0 i 1, a przerzutnik zmienia stan wcześniejszy na odwrotny;

• gdy C jest w stanie niskim, blokowane są stany wejściowe J i K.

4.6.3. Przerzutnik D

Przerzutnik D jest jednym z podstawowych przerzutników synchronicznych, zwa­nym również układem opóźniającym (rysunek 4.23). Przerzutnik ma jedno wejście D, służące do przepisywania jego stanu na wyjście Q z opóźnieniem jednego impulsu taktującego.

Rysunek 4.23.

Symbol przerzutnika D

Przerzutnik D składa się z czterech bramek NAND. Stanowi rozbudowaną wersję prze­rzutnika RS (rysunek 4.24).

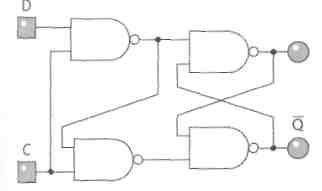
Rysunek 4.24.

q Budowa przerzutnika D

Działanie przerzutnika D opisuje tablica stanów:

D C Q

0 10

111
x 0 1

Przerzutnik D działa według następujących zasad:

• D = 1 i C = 1 — stan wysoki z wejścia D przepisany jest na wyjście Q;

• D = 0iC = l — stan niski z wejścia D przepisany jest na wyjście Q;

• stan niski na C powoduje zablokowanie wejścia D.

4.7. Liczniki

Licznik (ang. counter) zbudowany jest najczęściej z kilku równolegle lub szeregowo podłączonych przerzutników, a jego głównym zadaniem jest zliczanie i pamiętanie liczby impulsów podawanych na wejście zliczające (rysunek 4.25).

W zależności od kierunku zliczania wyróżniamy:

• liczniki zliczające w przód — po każdym impulsie wejściowym zwiększają licz­bę pamiętaną w liczniku o jeden;

• liczniki zliczające w tył — zmniejszają zawartość licznika o jeden;

• liczniki rewersyjne — dają możliwość wyboru kierunku zliczania.

Ze względu na sposób sterowania rozróżniamy:

• liczniki asynchroniczne (ang. asynchronous counter) — poszczególne przerzutni-ki sterowane są wyjściami przerzutników poprzedzających;

• liczniki synchroniczne (ang. synchronous counter) — przerzutniki zmieniają swój stan jednocześnie z taktem zegarowym.

Dostępne są gotowe układy scalone zawierające różne wersje liczników, na przykład TTL SN7493 — licznik asynchroniczny (rysunek 4.26), CMOS MCY 74029 — syn­chroniczny licznik rewersyjny itp.

Rysunek 4.26.

Schemat układu SN7493

4.8. Sumatory

Sumatory (ang. adders) są cyfrowymi układami kombinacyjnymi umożliwiającymi wykonywanie operacji sumowania liczb binarnych lub dziesiętnych. Najprostsze su­matory sumują pojedyncze liczby (rysunek 4.27). Kilka szeregowo lub równolegle po łączonych sumatorów może dokonywać obliczeń na liczbach wielopozycyjnych.

Rozróżnia się dwa główne rodzaje sumatorów:

• sumatory szeregowe (ang. serial adder), które podczas każdej operacji dodają dwa bity składników oraz bit przeniesienia;

• sumatory równoległe (ang. paralel adder), wielopozycyjne, składające się z kil­ku sumatorów jednobitowych. Wyróżnia się następujące odmiany sumatorów równoległych:

• z przeniesieniami szeregowymi (ang. ripple-carry adder) (rysunek 4.28)

— poszczególne pary bitów sumowane są za pomocą osobnych sumatorów, a przeniesienie wygenerowane na jednej pozycji przesyłane jest do sumatora pozycji następnej;

• z przeniesieniami równoległymi (ang. carry look-dhead adder) — wszystkie
przeniesienia wytwarzane są jednocześnie na podstawie bitów sumowanych
składników i przeniesienia początkowego.

Działanie sumatora jednobitowego przedstawia poniższa tabela stanów:

4.9. Rejestry

Rejestr (ang. register) jest układem cyfrowym służącym do zapamiętywania określonej porcji bitów danych. Każda pozycja rejestru przechowuje 1 bit informacji. Budowa rejestrów opiera się na przerzutnikach i bramkach logicznych połączonych w funkcjo­nalny układ logiczny (rysunek 4.29). Rejestry stosuje się tam, gdzie występuje potrze­ba chwilowego przechowania niewielkiej ilości informacji binarnej.

Rysunek 4.29. Rejestr szeregowy przesuwający z przerzutników JK

W zależności od sposobu wprowadzania danych oraz ich odczytywania wyróżnia się rejestry szeregowe i równoległe:

• Rejestry szeregowe umożliwiają szeregowe wprowadzenie i wyprowadzanie danych. Do grupy rejestrów szeregowych można zaliczyć rejestry przesuwające zbudowane z przerzutników D (rysunek 4.30) lub JK. Wpisywanie informacji do rejestru odbywa się bit po bicie w kolejnych taktach zegarowych z jednoczesnym przesuwem od wejścia do wyjścia.

• Rejestry równoległe umożliwiają równoległe wprowadzanie i wyprowadzanie danych jednocześnie do wszystkich pozycji rejestru.

4.10. Kodery i dekodery

Koder (enkoder) to cyfrowy układ kombinacyjny, którego zadaniem jest zamiana infor­macji z aktywnego wejścia na postać binarną na wyjściu. Kodery stosowane są najczę­ściej w konwerterach kodów (translatorach) zamieniających liczby w postaci dziesiętnej (na przykład wprowadzane z prostej klawiatury 10-klawiszowej) na postać dwójkową.

Przykładem układu scalonego zawierającego koder jest UCY74147 (rysunek 4.31) słu­żący do zamiany zanegowanego kodu „1 z 10"³ na zanegowany kod BCD⁴ (ang. Bina-ry-Coded Decimal— kod dziesiętny zakodowany dwójkowo).

Rysunek 4.31.

Schemat dekodera UCY74147

^J Sposób kodowania liczb (1 z „k"), gdzie słowa binarne o długości n (10) bitów zawierają zawsze tylko

jeden bit o wartości 1. ⁴ Sposób zapisu liczb polegający na zakodowaniu kolejnych cyfr dziesiętnych dwójkowo przy użyciu

czterech bitów.

Działanie układu 74147 prezentuje poniższa tabela stanów:

Dekoder jest układem kombinacyjnym realizującym działania odwrotne niż enkode tzn. sygnał w postaci binarnej zamieniany jest na postać dziesiętną. Na wejścia pod wane są liczby binarne w kodzie BCD, konwertowane na postać dziesiętną i wyprow dzone na jedną z 10 linii. Przykładem układu scalonego z dekoderem jest UCY7442 (rysunek 4.32).

4.11. Multipleksery i demultipleksery

Działanie układu 7442N prezentuje poniższa tabela stanów:
Zakodowana liczba Stan wejść Stan wyjść

4.11. Multipleksery i demultipleksery

Multiplekser ma szereg wejść, jedno wyjście, wejścia sterujące oraz wejście strobują-ce. Jeden wybrany stan na wejściu jest przełączany (komutowany) na wyjście, a nu­mer przełączanego wejścia podaje się w postaci liczby binarnej w kodzie BCD — po­przez wejścia sterujące. Wejście strobujące blokuje pracę multipleksera w momencie pojawienia się stanu wysokiego. Przykładem układu zawierającego multiplekser jest UCY74150N (rysunek 4.33).

Rysunek 4.33.

Schemat multipleksera UCY74150N

D C B A Działanie multipleksera UCY74150N prezentuje poniższa tabela stanów: Wejścia sterujące Wejścia strobujące Wyjście

Demultiplekser (rysunek 4.34) przełącza sygnał z wejścia na jedno z określonych wyjść (działanie odwrotne do multipleksera). Numer wyjścia podaje się za pomocą wejść sterujących w kodzie BCD, a blokowanie działania demultipleksera umożliwia wejście strobujące.

Rysunek 4.34. Schemat demultipleksera 4-wyjściowego

1. Projektowanie i testowanie działania półsumatora.

• Za pomocą programu Digital Works (lub podobnego) zaprojektuj bram­kę XOR zbudowaną z dwóch bramek NOT, dwóch AND i jednej OR.

• Na podstawie przygotowanej bramki XOR zbuduj półsumator.

• Przetestuj działanie półsumatora, tworząc tablicę prawdy.

• Wykonaj sprawozdanie z ćwiczenia.

2. Projektowanie i testowanie działania przerzutnika JK.

• Na podstawie schematu z niniejszego podręcznika zbuduj przerzutnik JK, wykorzystaj do tego program Digital Works (lub podobny).

• Przetestuj schemat logiczny i wypełnij tablicę prawdy uzyskanymi danymi empirycznymi.

• Wykonaj sprawozdanie z ćwiczenia.

3. Analiza oznaczeń układów scalonych.

• Przeprowadź analizę oznaczeń kilku układów scalonych zgodnych z normą BN-73/3375.

• Scharakteryzuj poszczególne układy na podstawie oznaczeń.

• Wykonaj sprawozdanie z ćwiczenia.

2^10	Kilo binarne	Ki	Kibi
220	Mega binarne	Mi	Mebi
230	Giga binarne	Gi	Gibi
240	Tera binarne	Ti	Tebi
250	Peta binarne	Pi	Pebi
260	Eksa binarne	Ei	Exbi
270	Zeta binarne	Zi	Zebi
280	Yotta binarne	Yi	Yobi

Działanie przerzutników RS opisują tabele stanów:

Rysunek 4.25. Licznik synchroniczny

Rysunek 4.27.

Sj Schemat logiczny

sumatora jednobitowego

Rysunek 4.28. Schemat sumatora równoległego z przeniesieniem szeregowym (ripple-carry adder)

Rysunek 4.30.

Schemat układu SN74175 z czterema przerzutnikami D, umożliwiający zbudowanie rejestru

Rysunek 4.32.

Symbol dekodera UCY7442N

---