Definicja zdania

Zdaniem w logice nazywamy wypowiedź zbudowaną zgodnie z zasadami ustalonego języka, której można przypisać jednoznacznie jedną z dwu ocen: prawdę lub fałsz -nazywane wartościami logicznymi danego zdania i oznaczane odpowiednio symbolami
,
.

Definicja formy zdaniowej

Formą zdaniową nazywamy wypowiedź, która może zawierać zmienne, zbudowaną według takich samych reguł gramatycznych jak zdanie. Fakt, że
jest zmienną formy zdaniowej
oznaczamy pisząc
.

Uwaga 1. Każde zdanie jest formą zdaniową.

Uwaga 2. Istnieją formy zdaniowe nie będące zdaniami.

Zasada tworzenia zdań z form zdaniowych

Z formy zdaniowej można otrzymać zdanie na dwa sposoby:

1. Przez podstawienie w miejsce zmiennych, obiektów w stosunku do których będziemy mogli stosować oceny logiczne prawdziwości i fałszu.

2. Przez stosowanie kwantyfikatorów w odniesieniu do występujących w formie zdaniowej zmiennych. Stosowanie kwantyfikatora dużego do formy
   oznacza utworzenie zdania
   , które czytamy: „ dla każdego elementu
   ze zbioru
   jest
   ”. Stosowanie kwantyfikatora małego do formy
   oznacza utworzenie zdania
   , które czytamy: „ istnieje element
   ze zbioru
   taki, że
   ”.

Definicja

Jeśli zakresem zmienności zmiennej
w formie
jest zbiór
, to zbiór tych wszystkich elementów zbioru
, które podstawione w miejsce zmiennej
w formie
dają zdanie prawdziwe oznaczamy jako
.

Przykład. Przedział domknięty
gdzie
,
są liczbami rzeczywistymi takimi, że
można zapisać jako
.

Zasada weryfikacji prawdziwości zdań złożonych

Oceny prawdziwości zdań złożonych dokonujemy na podstawie informacji o prawdziwości ich składników zgodnie z następującymi ustaleniami:

1	1	0	1	1	1	1
1	0	0	0	1	0	0
0	1	1	0	1	1	0
0	0	1	0	0	1	1

2. 
   jest prawdą wtedy i tylko wtedy gdy
   


jest prawdą wtedy i tylko wtedy gdy





Definicja tautologii

Prawem logicznym albo tautologią nazywamy zdanie złożone, które jest prawdziwe niezależnie od wartości logicznych zdań składowych.

Wykaz ważniejszych tautologii

Zasada prowadzenia dowodu

Każdy element rozumowania zwanego dowodem w dowolnej teorii matematycznej daje się uzasadnić tautologią albo aksjomatem tej teorii.

Definicja iloczynu kartezjańskiego zbiorów

Iloczynem kartezjańskim zbiorów
i
nazywamy zbiór wszystkich par uporządkowanych
takich, że
i
. Iloczyn kartezjański zbiorów
i
oznaczamy jako
.

Definicja funkcji

Każdy podzbiór
iloczynu kartezjańskiego
zbiorów
i
nazywamy funkcją odwzorowującą zbiór
w zbiór
o ile spełnia on następujące dwa warunki:

1. 
   

2. 
   .

Fakt, że
jest funkcją odwzorowującą zbiór
w zbiór
oznaczamy pisząc
. Zbiór funkcji odwzorowujących
w
oznaczamy jako
.

Definicja funkcji różnowartościowej

Jeśli
to mówimy, że
jest różnowartościowa jeśli spełnia następujący warunek:







Definicja funkcji odwzorowującej zbiór X na zbiór Y

Jeśli
to mówimy, że
odwzorowuje zbiór
na zbiór
jeśli spełnia następujący warunek:


.

Definicja funkcji wzajemnie jednoznacznej

Jeśli
to mówimy, że
jest funkcją wzajemnie jednoznaczną jeśli jest funkcją różnowartościową odwzorowującą zbiór
na zbiór
.

Definicja funkcji odwrotnej

Niech
będzie funkcją wzajemnie jednoznaczną. Wówczas zbiór
jest funkcją wzajemnie jednoznaczną odwzorowującą zbiór
na zbiór
. Nazywamy go funkcją odwrotną do funkcji
i oznaczamy jako
.

Definicja złożenia funkcji

Niech
,
przy czym
. Zbiór
jest funkcją odwzorowująca zbiór
w zbiór
. Nazywamy go złożeniem funkcji
i
i oznaczamy jako
.

Definicja obrazu zbioru przez funkcję

Niech
. Dla dowolnego zbioru
zbiór
nazywamy obrazem zbioru
przez funkcję
i oznaczamy jako
.

Definicja przeciwobrazu zbioru przez funkcję

Niech
. Dla dowolnego zbioru
zbiór
nazywamy przeciwobrazem zbioru
przez funkcję
i oznaczamy jako
.

Definicja dziedziny i zbioru wartości funkcji

Niech f : X → Y. Wówczas zbiór X nazywamy dziedziną funkcji i oznaczamy jako Df natomiast f[X] nazywamy zbiorem wartości funkcji i oznaczamy jako Wf.

Przykłady rodzin funkcji

Niech f : X → Y.

• Jeśli X ⊂ R i Y = R, to funkcję f nazywać będziemy funkcją rzeczywistą zmiennej rzeczywistej.

• Jeśli X = N i Y = R, to funkcję f nazywać będziemy nieskończonym ciągiem liczbowym o wyrazach rzeczywistych.

• Jeśli X = N i Y = N i f jest funkcją wzajemnie jednoznaczną, to f nazywać będziemy permutacją zbioru liczb naturalnych.

• Jeśli X = {1, 2, ..., m}×{1, 2, ..., n} oraz Y = R, to funkcję f nazywać będziemy macierzą o m wierszach i n kolumnach.




Ciągłość. Niech x₀ ∈ R.

Definicja otoczenia, sąsiedztwa i punktu skupienia

Niech a, b ∈ R i a < x₀ < b. Otoczeniem (otoczeniem lewostronnym, prawostronnym) punktu x₀ nazywamy przedział (a, b) ((a, x₀], [x₀ , b)). Rodzinę zbiorów będących otoczeniami (otoczeniami lewostronnymi, prawostronnymi) punktu x₀ oznaczać będziemy symbolem O(x₀) (O ^-(x₀), O⁺(x₀)). Każdy zbiór postaci U \ {x₀}, gdzie U ∈ O(x₀) (U ∈ O ^-(x₀), U ∈ O⁺(x₀)) nazywać będziemy sąsiedztwem (sąsiedztwem lewostronnym, prawostronnym) punktu x₀. Rodzinę zbiorów będących sąsiedztwami (sąsiedztwami lewostronnymi, prawostronnymi) oznaczać będziemy symbolem S(x₀) (S ^-(x₀), S⁺(x₀)).

Niech X ⊂ R. Mówimy, że x₀ jest punktem skupienia (lewostronnym, prawostronnym punktem skupienia) zbioru X, jeśli


(
,
).

Zbiór punktów skupienia (lewostronnych, prawostronnych punktów skupienia) zbioru X oznaczamy jako X^d (X^d-, X^d+).

Niech f będzie funkcją rzeczywistą zmiennej rzeczywistej.

Definicja granicy funkcji

Niech x₀ ∈ (Df)^d (x₀ ∈ (Df)^d-, x₀ ∈ (Df)^d+ ). Mówimy, że g ∈ R jest granicą (granicą lewostronną, prawostronną) funkcji f w punkcie x₀, gdy


(
,
).

Fakt, że g jest granicą (granicą lewostronną, prawostronną) zapisujemy symbolicznie


(
,
).

Definicja ciągłości funkcji

Niech x₀ ∈ Df.

f jest ciągła w x₀ ⇔ x₀ ∉ (Df)^d ∨


f jest lewostronnie ciągła w x₀ ⇔ x₀ ∉ (Df)^d- ∨


f jest prawostronnie ciągła w x₀ ⇔ x₀ ∉ (Df)^d+ ∨


Niech X ⊂ R. Mówimy, że f jest ciągła w zbiorze X, gdy jest ciągła w każdym punkcie tego zbioru. Zbiór punktów ciągłości funkcji f oznaczać będziemy przez Cf.

Uwaga. Funkcja jest ciągła w punkcie x₀ wtedy i tylko wtedy, gdy jest ciągła lewostronnie i prawostronnie w tym punkcie.

Rodzaje nieciągłości - definicja

Niech x₀ ∈ Df. Mówimy, że x₀ jest punktem nieciągłości pierwszego rodzaju funkcji f, jeśli istnieją i są skończone granice
,
przy czym
lub
Mówimy, że x₀ jest punktem nieciągłości drugiego rodzaju, jeśli x₀ ∉ Cf i x₀ nie jest punktem nieciągłości pierwszego rodzaju.

Twierdzenia o funkcjach ciągłych

Twierdzenie Weierstrassa-Darboux. Niech a, b ∈ R, a < b, [a, b] ⊂ Cf. Wówczas funkcja f jest ograniczona na [a, b]. Ponadto

1. 
   ;

2. 
   ;

3. 
   

Twierdzenie o klasie funkcji ciągłych

Funkcje elementarne są ciągłe. Działania algebraiczne wykonywane na funkcjach ciągłych dają funkcje ciągłe. Złożenia funkcji ciągłych są funkcjami ciągłymi. Funkcje odwrotne do funkcji ciągłych (o ile istnieją) też są funkcjami ciągłymi.

Uwaga. Jeśli x₀ ∈ Cf i f(x₀) > 0, to


Definicja ciągłości jednostajnej

Niech X ⊂ Df. Mówimy, że funkcja f jest jednostajnie ciągła na X, jeśli




Uwaga. Jeśli f jest jednostajnie ciągła na zbiorze X, to jest ciągła w każdym punkcie tego zbioru.

Uwaga. Istnieją funkcje ciągłe w każdym punkcie zbioru X lecz nie będące jednostajnie ciągłymi na tym zbiorze.

Uwaga. Funkcja ciągła na przedziale domkniętym i ograniczonym jest na tym przedziale jednostajnie ciągła.

SZEREGI LICZBOWE

Definicja szeregu

Niech
będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg
gdzie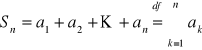
. Taki szereg liczbowy oznaczamy symbolem
. Liczbę
nazywamy n-tym wyrazem, a liczbę
- n-tą sumą tego szeregu.

Definicja szeregu zbieżnego, rozbieżnego i sumy szeregu

Mówimy, że szereg
jest zbieżny jeśli ciąg
jest zbieżny do granicy skończonej zwanej w tym przypadku sumą szeregu i oznaczanej symbolem identycznym z symbolem szeregu.

Mówimy, że szereg
jest rozbieżny gdy nie jest zbieżny.

Twierdzenie o kombinacji liniowej szeregów

Jeśli szeregi
,
są zbieżne odpowiednio do liczb
i
, to dla dowolnych liczb rzeczywistych
,
zbieżny jest również szereg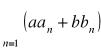
przy czym suma tego szeregu wynosi
.

Twierdzenie o zbieżności szeregu geometrycznego

Szereg
zwany szeregiem geometrycznym o podstawie
jest zbieżny wtedy i tylko wtedy gdy
.

Twierdzenie o zbieżności szeregu harmonicznego

Szereg
zwany szeregiem harmonicznym rzędu
jest zbieżny wtedy i tylko wtedy gdy
.

Warunek konieczny zbieżności szeregu

Jeśli szereg
jest zbieżny to
.

Niech
i
oznaczają szeregi liczbowe.

Uwaga. Jeśli ciągi
i
różnią się skończoną ilością wyrazów, to oba szeregi
i
są jednocześnie zbieżne lub rozbieżne.

KRYTERIA ZBIEŻNOŚCI SZEREGÓW

Kryterium porównawcze

Jeśli
to ze zbieżności szeregu
wynika zbieżność szeregu
i z rozbieżności szeregu
wynika rozbieżność szeregu
.

Kryterium ilorazowe

Jeśli
oraz
, to oba szeregi
i
są jednocześnie zbieżne lub rozbieżne.

Kryterium Cauchy'ego

Jeśli
to
jest zbieżny gdy
i rozbieżny gdy
.

Kryterium d'Alemberta

Jeśli
oraz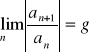
to szereg
jest zbieżny gdy
i rozbieżny gdy
.

Kryterium Raabego

Jeśli
oraz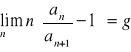
to szereg
jest zbieżny gdy
i rozbieżny gdy
.

Twierdzenie o zagęszczaniu

Jeśli
jest ciągiem nierosnącym o wyrazach nieujemnych to szeregi
i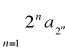
są jednocześnie zbieżne lub rozbieżne.

Kryterium Dirichleta

Jeśli ciąg sum częściowych szeregu
jest ograniczony oraz
jest ciągiem nierosnącym zbieżnym do zera to szereg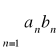
jest zbieżny.

Kryterium Abela

Jeśli szereg
jest zbieżny i ciąg
jest monotoniczny i ograniczony, to szereg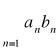
jest zbieżny.

Kryterium Leibniza

Jeśli
jest ciągiem nierosnącym zbieżnym do 0, to szereg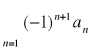
zwany szeregiem naprzemiennym jest zbieżny.

Definicja zbieżności bezwzględnej

Mówimy, że szereg
jest bezwzględnie zbieżny, gdy zbieżny jest szereg
.

Uwaga Każdy szereg zbieżny bezwzględnie jest zbieżny.

Uwaga Istnieją szeregi zbieżne lecz nie bezwzględnie zbieżne.

Definicja szeregu zbieżnego warunkowo

Szereg zbieżny lecz nie bezwzględnie zbieżny nazywamy szeregiem zbieżnym warunkowo.

Twierdzenie

Jeśli szereg
jest bezwzględnie zbieżny, to dla dowolnej permutacji
liczb naturalnych szereg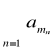
jest zbieżny i ma taką samą sumę jak szereg
.

Twierdzenie Cauchy'ego

Jeśli szeregi
i
są bezwzględnie zbieżne, to szereg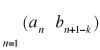
jest zbieżny przy czym suma tego szeregu wynosi
gdzie
oznacza sumę szeregu
, a
sumę szeregu
.

Twierdzenie Riemanna

Niech
będzie szeregiem warunkowo zbieżnym. Dla dowolnego
istnieje permutacja
zbioru liczb naturalnych taka, że
jest sumą szeregu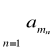
.

CIĄGI I SZEREGI FUNKCYJNE

Przyjmijmy, że
.

Definicja ciągu funkcyjnego

Ciągiem funkcyjnym określonym na zbiorze
nazywamy każdą funkcję odwzorowującą zbiór
w zbiór
. Załóżmy, że
. Wówczas dla oznaczenia ciągu funkcyjnego, którego n-tym wyrazem jest funkcja
używamy oznaczenie
.

Niech
oznacza ciąg funkcyjny taki, że
. Niech
.

Definicja zbieżności punktowej ciągu funkcyjnego

Mówimy, że ciąg
jest punktowo zbieżny na zbiorze
do funkcji
jeśli
.

Definicja zbieżności jednostajnej ciągu funkcyjnego

Mówimy, że ciąg
jest jednostajnie zbieżny na zbiorze
do funkcji
jeśli
.

Fakt, że
jest punktowo zbieżny do funkcji
na zbiorze
oznaczamy pisząc
.

Fakt, że
jest jednostajnie zbieżny do funkcji
na zbiorze
oznaczamy pisząc


.

Twierdzenie

Jeśli


to
.

Uwaga Twierdzenie odwrotne nie jest prawdziwe.

Twierdzenie Weierstrassa

Niech
dla
. Wówczas


Twierdzenie

Jeśli
i
jest ciągła na X, to również f jest ciągła na X.

Definicja funkcji przedziałami liniowej

Niech
,
i niech
. Funkcję f nazywamy przedziałami liniową na przedziale
jeśli f jest ciągła na
oraz jeśli istnieją układy liczb
oraz
oraz
takie, że


Twierdzenie

Każda funkcja ciągła w przedziale domkniętym jest granicą jednostajnie zbieżnego ciągu funkcji przedziałami liniowych na tym przedziale.

Definicja szeregu funkcyjnego

Niech
będzie ciągiem funkcyjnym takim, że
. Szeregiem funkcyjnym nazywamy ciąg funkcyjny
gdzie
. Taki szereg funkcyjny oznaczamy symbolem
. Funkcję
nazywamy n-tym wyrazem a funkcję
nazywamy n-tą sumą tego szeregu.

Definicja zbieżności punktowej i jednostajnej szeregu funkcyjnego

Szereg funkcyjny
jest punktowo (jednostajnie) zbieżny na zbiorze X gdy ciąg funkcyjny
jest punktowo (jednostajnie) zbieżny na tym zbiorze.

Funkcję będącą granicą ciągu funkcyjnego
o ile ona istnieje nazywamy sumą szeregu
i oznaczamy tak jak sam szereg.

Wniosek. Szereg funkcyjny
jest punktowo zbieżny na zbiorze X wtedy i tylko wtedy gdy
jest zbieżny.

Wniosek. Jeśli szereg funkcyjny
jest jednostajnie zbieżny na zbiorze X, to jest punktowo zbieżny na tym zbiorze.

Twierdzenie Weierstrassa

Niech
będzie szeregiem funkcyjnym funkcji określonych na zbiorze X, a
szeregiem liczbowym zbieżnym takim, że
.

Wówczas szereg
jest jednostajnie zbieżny oraz
jest bezwzględnie zbieżny.

Definicja szeregu potęgowego

Niech
i niech
dla
. Załóżmy, że


jest funkcją taką, że



jest funkcją taką, że
dla
i
.

Szereg funkcyjny
nazywamy szeregiem potęgowym o środku w punkcie
i współczynnikach
. Oznaczamy go symbolicznie jako
.

Definicja promienia zbieżności szeregu potęgowego

Liczbę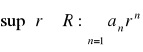
nazywamy promieniem zbieżności szeregu potęgowego
.

Uwaga. Promień zbieżności szeregu potęgowego nie zależy od jego środka
a jedynie od współczynników
dla
.

Uwaga. Promień zbieżności szeregu potęgowego jest zawsze liczbą nieujemną.

Niech R oznacza promień zbieżności szeregu potęgowego
.




Twierdzenie Cauchy'ego - Hadamarda

1. Jeśli
   , to
   

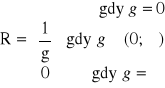
2. Jeśli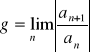
   , to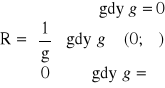
   

Twierdzenie o punktach zbieżności szeregu potęgowego

Jeśli R = 0, to szereg
jest zbieżny jedynie dla
.

Jeśli R = ∞, to szereg
jest zbieżny bezwzględnie dla dowolnego
.

Jeśli R
, to szereg
jest zbieżny bezwzględnie dla dowolnego
oraz rozbieżny dla
.

Definicja przedziału zbieżności szeregu potęgowego

Przedziałem zbieżności szeregu
nazywamy zbiór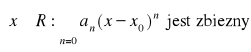


Twierdzenie

Szereg potęgowy
jest zbieżny jednostajnie w każdym przedziale domkniętym zawartym w przedziale zbieżności szeregu potęgowego.

8