Zadania do tematu: Charakterystyki częstotliwościowe układów złożonych

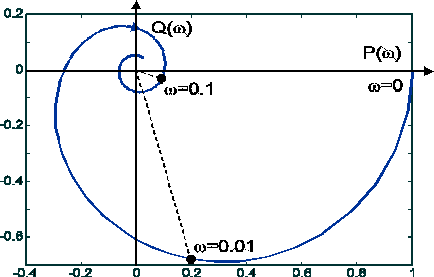
Zadanie 1. Transmitancję obiektu w układzie regulacji przedstawiono w postaci szeregowego połączenia członu inercyjnego i członu z opóźnieniem (rys.1). Wyznaczyć charakterystykę amplitudowo-fazową (wykres Nyquista P-Q) oraz charakterystyki logarytmiczne (wykresy Bodego) obiektu, jeśli stała czasowa T=100s, a czas opóźnienia T0=50s.

Rys.1

Zadanie 2. Dane jest równanie różniczkowe obiektu wchodzącego w skład pewnego układu regulacji w postaci

,

gdzie T0 jest czasem opóźnienia sygnału wejściowego. Wyznaczyć charakterystyki częstotliwościowe dla T=2s, T0 =0.5s, k=10, =0.5.

Zadanie 3. Wyznaczyć parametry k,Ti regulatora PI o transmitancji
, aby po szeregowym połączeniu go z obiektem (jak na rys.1) o asymptotycznej charakterystyce amplitudowej pokazanej na rys.2 otrzymać zadaną charakterystykę układu otwartego
. Wyznaczyć transmitancje oraz charakterystyki fazowe obiektu i układu z regulatorem zakładając, że są one minimalnofazowe.

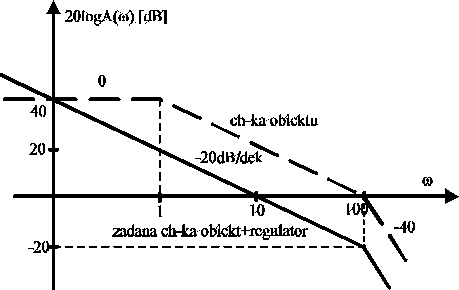
Rys.2

Zadanie 4. Na rys.3 przedstawiono schemat blokowy pewnego układu regulacji. Transmitancje operatorowe poszczególnych członów mają postać

(regulator PI),
(obiekt),

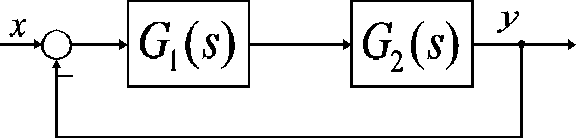
Rys.3

Wyznaczyć charakterystykę amplitudowo-fazową oraz charakterystyki logarytmiczne układu zamkniętego.

Zadanie 5.Wyznaczyć charakterystyki logarytmiczne (asymptotyczne) układu o transmitancji

dla k=100, T1 =40s, T2 =2s, T3 =0.1s.

Zadanie 6. Na rys.4 przedstawiono asymptotyczną amplitudową charakterystykę logarytmiczną pewnego układu dynamicznego. Na jej podstawie wyznaczyć transmitancję G(s) układu, jeżeli wiadomo, że jest on minimalnofazowy.

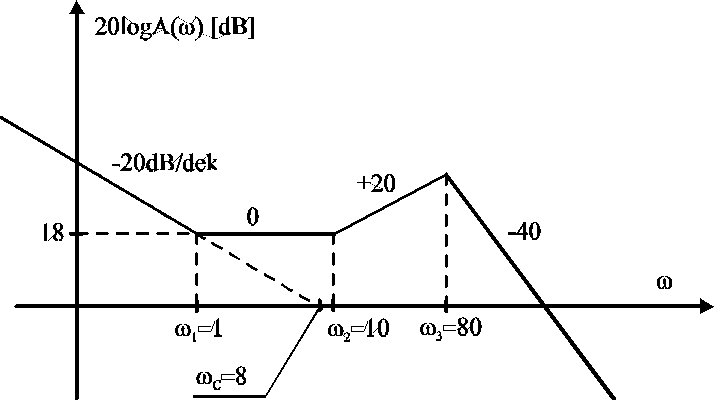
Rys.4

UWAGA: Układami minimalnofazowymi nazywa się układy, których transmitancja ma postać funkcji wymiernej, której zera i bieguny znajdują się w lewej półpłaszczyźnie. Charakterystyka fazowa dla
dąży wtedy do wartości stałej, zwykle najmniejszej.

Odpowiedzi

1.

2.

3.
.

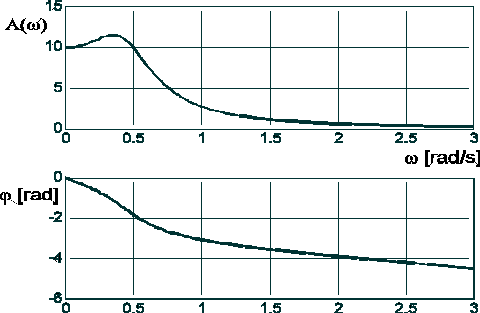
4. Układ oscylacyjny II rzędu o charakterystyce opisanej wzorami: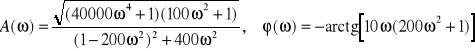

6.

---