Wyższa Szkoła Technologii Informatycznych

Laboratorium Elektroniki - Ćwiczenie nr 2
Temat:	Badanie obwodów prądu przemiennego
Prowadzący:	Wiktor Olchowik
Data wykonania	09.04.2007
Skład zespołu:	Paulina Wojda - ID-2/II Paweł Krawczyk - ID-2/II

Program ćwiczenia

1. Pomiary przebiegów prądu przemiennego

Ćwiczenie pozwala zaobserwować wpływ kształtu przebiegu na wartość średnią i skuteczną.

Rys.1. Układ do pomiaru przebiegów prądu przemiennego.

Tabele 1. Tabela pomiarów z obliczonymi teoretycznymi wartościami skutecznymi dla zadanych amplitud.

Tabela pomiarów 1
f[Hz]		Trójkąt[V]	Sinusoida[V]	Prostokąt[V]
50	Vamp	4,41	4,6	4,8
		Usk	3,219	2,562	5,33
		Usk(obl.)	2,546114687	3,252691193	4,8
	500	Vamp	4,5	4,8	4,9
		Usk	3,217	5,33	5,3
		Usk(obl.)	2,598076211	3,39411255	4,9

Wnioski:

Na podstawie przeprowadzonych pomiarów można twierdzić, że przyjęta przez nas metoda obliczenia wartości skutecznych napięć prądu przemiennego jest dobra. Niestety nasze pomiary miały sens jedynie dla prądu o przebiegu sinusoidalnym, bowiem mierniki uniwersalne mają wyskalowaną wartość skuteczną dla tego przebiegu. W przypadku przebiegów trójkątnego i prostokątnego pojawiają się dość duże błędy na miernikach. Dodatkowo dla przebiegu prostokątnego występowały przeregulowania, przez co zmuszeni zostaliśmy do wprowadzenia sprzężenia DC i odczytywania wartości Vamp, nie zaś V max. Dlatego wartość skuteczna wskazana przez miernik okazała się większa od wartości maksymalnej, co oczywiście nie jest zgodne z prawdą.

Pomiary napięć w obwodzie prądu przemiennego RC.

Rys.2. Układ RC

Tabela 2. Wartości zmierzone i obliczone wartości kąta przesunięcia fazowego.

F [Hz]	Ug [V]	Ur [V]	Uc [V]	Ugamp [V]	Uramp [V]	Δt [μs]	φ[^o]
50	3,551	2,004	2,924	4,9	2,8	-3,02	-0,05436
200	3,49	3,277	1,193	4,88	4,5	-280	-20,16

R[kΩ]

2,17

C[ F]

1,026

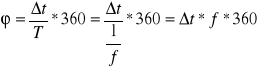
Wykres wskazowy wartości skutecznych:

Dla częstotliwości f=50Hz

U_G - napięcie odniesienia

I - natężenie prądu w obwodzie

Z_Z - impedancja zastępcza obwodu

Obliczenia:

Dla częstotliwości f=50Hz

=314,1592654

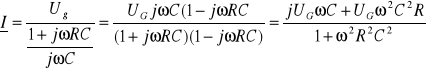
2,384 - j1,667

1,665 + j 1,667

2,909[V]

2,035[V]

[V]

Dla częstotliwości f=200Hz:

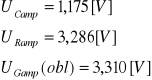
Wykres wskazowy

Wnioski:

Z przeprowadzonych pomiarów obliczeń wynika, że różnice między wynikami uzyskami różnymi metodami są niewielkie. Ewentualne błędy mogą wynikać z niedokładności mierników, oscyloskopu oraz zaokrągleń podczas procesu obliczeniowego. W przypadku kąta przesunięcia fazowego podczas obliczeń uzyskaliśmy wartość dodatnią. Wynika to z odczytu na oscyloskopie, bowiem tam przebiegiem odniesienia był przebieg z generatora, natomiast napięcie to jest opóźnione w fazie względem prądu, a zatem względem napięcia na rezystancji.

Wielkość wiążąca prąd i napięcie na kondensatorze nazywa się reaktancją, która jest tym mniejsza, im większa jest pojemność kondensora i częstotliwości prądu. Dlatego też dla większych wartości pulsacji obserwujemy mniejszy spadek napięcie na kondensatorze.

3. Pomiary napięć w obwodzicie prądu przemiennego RL.

Rys.3. Układ RL

Tabela 3.

f [kHz]	UG [V]	UR [V]	UC [V]	Ugamp [V]	Uramp [V]	Δt [μs]	φ [^o]
10				4,085	3,54	95,5	343,8
100				4,835	1,59	8,05	289,8

R[Ω]

199,5

L[mH]

1

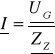
Dla częstotliwości 10 kHz:

Wykres wskazowy:

Dla częstotliwości 100 kHz:

Wnioski:

W przypadku obwodu RL również różnice między wielkościami zmierzonymi i obliczonymi są niewielkie, co potwierdza, że zastosowane metody obliczeń są dobre. Błędy wynikają głównie z niedokładności mierników oraz licznych zaokrągleń podczas obliczeń.

Dla prądu stałego cewka jest elementem rezystancyjnym o wartości zależnej od rezystancji przewodnika, z którego jest wykonana. Dla prądu o pewnej pulsacji różnej od zera, wykasuje inną wartość oporu, nazywaną reaktancją. Reaktancja jest tym większa, im większa indukcyjność i pulsacja prądu. Dlatego tez dla większych wartości częstotliwości f, obserwujemy większy spadek napięcie na cewce.

---