Politechnika Częstochowska

Wydział Elektryczny

Magisterskie Studia Uzupełniające

LABORATORIUM

GOSPODARKA ELEKTROENERGETYCZNA

Ćwiczenie: Wykorzystanie programowania transportowego w elektroenergetyce

Wykonał:

Krystek Szymon

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z klasycznym zagadnieniem transportowym na przykładzie zadania 1 z elektrowniami. Celem jest wybór takiego planu przewozów, który minimalizowałby łączny koszt transportu w ustalonym horyzoncie czasowym.

Zadanie.1

Trzy elektrownie należące do jednego koncernu energetycznego zasilają węzeł sieciowy (GPZ Główny Punkt Zasilający). Chwilowe zapotrzebowanie na moc w GPZ wynosi 200 MW przy cosϕ=0,8. Zakładając, że każda elektrownia może pokryć powyższe zapotrzebowanie, wyznaczyć wartości mocy dosłanych do węzła GPZ z elektrowni E1, E2 i E3, minimalizujących straty mocy czynnej w sieci przesyłowej. Dane linii przesyłowych:

L1: E1-GPZ U_n=110 kV, l₁=84 km, S₁=240 mm², γ=35 MS/m,

L2: E2-GPZ U_n=110 kV, l₂=84 km, S₂=120 mm², γ=35 MS/m,

L3: E3-GPZ U_n=110 kV, l₃=136,5 km, S₃=520 mm², γ=35 MS/m

2. Wprowadzenie do obliczeń

Zadanie można rozwiązać dwoma metodami:

I. Metoda kąta północno-zachodniego

Wypełnianie macierzy przewozów
rozpoczyna się od klatki w lewym górnym rogu. Wpisujemy do niej mniejszą z liczb
odpowiadających tej klatce, a następnie przesuwamy się w prawo lub w dół: w prawo, gdy produkt pierwszego dostawcy nie został jeszcze całkowicie rozdysponowany, a w dół, gdy całą podaż tego dostawcy rozdzielono odbiorcom.

II. Metoda minimalnego elementu macierzy

Polega na rozmieszczeniu przewozów przede wszystkim na tych trasach, na których koszty są najniższe. Punktem wyjścia jest przekształcenie macierzy kosztów do takiej postaci, by w każdym wierszu i w każdej kolumnie występowało co najmniej jedno zero. Można to uzyskać odejmując od elementów poszczególnych wierszy macierzy kosztów najmniejszy element znajdujący się w danym wierszu, a następnie od poszczególnych kolumn otrzymanej macierzy odejmując element najmniejszy znajdujący się w danej kolumnie. Rozmieszczenie przewozów od dowolnej klatki, w której wartość równa 0.

Jeśli uda się rozmieścić przewozy wyłącznie w klatkach, w których występują zera, to otrzymane rozwiązanie jest już optymalnym planem przewozów. Jeżeli nie, to należy je poprawiać stosując algorytm transportowy.

Model:

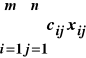
przy warunkach:

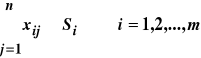
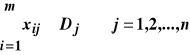
Tablica transportowa

Odbiorca	1	2	...	n	Podaż
Dostawca
1	c11	c12	...	c1n	S1
2	c21	c22	...	c2n	S2
...	...	...	...	...	...
m	cm1	cm2	...	cmn	Sm
Popyt	D1	D2	...	Dn

Rozwiązanie dopuszczalne modelu, gdy spełniony warunek:

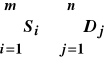
W standardowym modelu transportowym wygodnie jest przyjąć, że łączna podaż równa jest łącznemu popytowi:

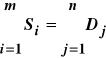
W tym celu tworzymy fikcyjny kierunek przewozu (fikcyjnego odbiorcę), którego zapotrzebowanie równe jest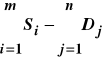
i oznaczając go numerem n przyjmujemy
, natomiast
oznaczać będzie tę część produkcji, która pozostanie u i-tego dostawcy.

3. Obliczenia za pomocą programu Excel

Zadanie zostało policzone przy pomocy dodatku „Solver”, w którym należało wprowadzić pewne ograniczenia oraz stworzyć formuły potrzebne do obliczenia zadania co przedstawia poniższa tabela.

W wyniku wprowadzenia danych z zadania 1 otrzymaliśmy rozwiązanie zadania oraz raport wyników.

	Wielkość przewozu z zakładu x do magazynu y (na przecięciu):
Elektrociepłownie	Razem	EC1	EC2	EC3	EC4
K1	900	0	400	0	500
K2	900	0	200	700	0
K3	800	500	0	0	300
		---	---	---	---
Razem:		500	600	700	800
	Popyt -->	500	600	700	800
Zakłady:	Podaż	Koszty przewozu z zakładu x do magazynu y (na przecięciu):
K1	900	113	113	111	110
K2	900	108	104	102	103
K3	900	114	117	116	114
Koszt przewozu:	283600	57000	66000	71400	89200

Komórka celu (Min)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$F$12	Razem: ---	800	800
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$C$8	K1 EC1	0	0
	$D$8	K1 EC2	400	400
	$E$8	K1 EC3	0	0
	$F$8	K1 EC4	500	500
	$C$9	K2 EC1	0	0
	$D$9	K2 EC2	200	200
	$E$9	K2 EC3	700	700
	$F$9	K2 EC4	0	0
	$C$10	K3 EC1	500	500
	$D$10	K3 EC2	0	0
	$E$10	K3 EC3	0	0
	$F$10	K3 EC4	300	300

Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$B$8	K1 Razem	900	$B$8<=$B$16	Wiążące	0
	$B$9	K2 Razem	900	$B$9<=$B$17	Wiążące	0
	$B$10	K3 Razem	800	$B$10<=$B$18	Nie wiążące	100
	$C$12	Razem: ---	500	$C$12>=$C$14	Wiążące	0
	$D$12	Razem: ---	600	$D$12>=$D$14	Wiążące	0
	$E$12	Razem: ---	700	$E$12>=$E$14	Wiążące	0
	$F$12	Razem: ---	800	$F$12>=$F$14	Wiążące	0

4. Wnioski

Z rozwiązanego zadania można wywnioskować, że łączny koszt przewozu wyniesie 283.600,00zł. Jest to najbardziej optymalny plan przy którym koszty transportu są zminimalizowane w pewnym okresie czasu.

Problem w tym zadaniu dotyczył wysłania wyrobów z trzech fabryk do czterech elektrociepłowni. Wyroby mogą być wysłane z dowolnej fabryki do dowolnej elektrociepłowni. Komórki zaznaczone w ramce kolorem brązowym określają ograniczenia, komórki zaznaczone na różowo to zmienne, a komórka niebieska jest komórką celu.

1

---