SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ

Katedra Techniki Pożarniczej

Zakład Hydromechaniki i Przeciwpożarowego Zaopatrzenia

Wodnego

LABORATORIUM HYDROMECHANIKI

ĆWICZENIE NR 5

TEMAT: STRATY LOKALNE I NA DŁUGOŚCI W RURACH GŁADKICH

WARSZAWA, sierpień 1998

PODSTAWY TEORETYCZNE

1. Współczynnik strat na długości.

Podczas przepływu cieczy lub gazu rurociągiem następuje spadek energii mechanicznej na korzyść energii cieplnej wywołany istnieniem lepkości. Ćwiczenie dotyczy określenia tego spadku dla ustalonego przepływu cieczy, poziomym prostoliniowym odcinkiem przewodu o stałej średnicy.

Stwierdzono doświadczalnie, że z dwóch składników energii mechanicznej, które mogłyby się zmieniać tj. energii kinetycznej i energii potencjalnej ciśnienia (energia potencjalna wzniesienia jest stała, ponieważ badany odcinek rurociągu jest poziomy) spada tylko energia ciśnienia, natomiast pierwszy z wymienionych składników pozostaje stały. Fakt ten jest zgodny z przewidywaniami teoretycznymi. Mianowicie, z równania ciągłości, które w tym przypadku ma postać:

(1)

gdzie:

ρ - gęstość płynu,

F - przekrój przewodu,

v_śr - średnia prędkość cieczy w rozpatrywanym przekroju, (wynika, że v_śr=const, przy założeniu nieściśliwości płynu i stałości przekroju F),

Wielkość omawianego spadku ciśnienia p zależy od następujących czynników:

1. Parametrów geometrycznych rury:

• średnicy wewnętrznej - d_w,

• długości - l, na której występuje spadek ciśnienia,

• chropowatości wewnętrznej powierzchni - k,

2. Stałych fizycznych cieczy:

• lepkość - 

• gęstość -ρ

3. Wielkości charakteryzujących ruch płynu, a mianowicie od stałej prędkości v_śr,

W ogólnym przypadku zależność tę można zapisać w następującej formie:

Δp=f(d_w, l, k, , ρ, v_śr) (2)

Na podstawie wyników analizy wymiarowej, a w szczególności na mocy tzw. twierdzenia  -zależność (2) można wyrazić w postaci bezwymiarowej:

(3)

gdzie wyrażenie
jest odwrotnością liczby Reynoldsa Re.

Badania doświadczalne wykazały, że spadek ciśnienia jest proporcjonalny do długości przewodu - przy zachowaniu stałych wartości pozostałych parametrów - mamy zatem

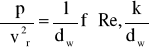
(4)

Oznaczmy:

(5)

gdzie:  - tzw. współczynnik strat na długości.

Graficznie funkcja (5) przedstawiono na wykresie Nikuradsego (rys.1.)

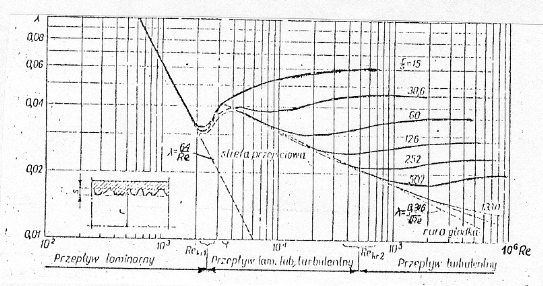
Rys.1. Wykres Nikuradsego: wpływ szorstkości na przebieg (Re)

Wykorzystując wprowadzone oznaczenie otrzymano ostatecznie

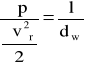
(6)

Z równania (6) wynikają następujące wnioski:

1. dla rury gładkiej współczynnik  jest funkcją tylko liczby Reynoldsa,

1. dla przepływów podobnych dynamicznie wielkość współczynnika  jest jednakowa i niezależna od rodzaju płynącej cieczy,

Wprowadzając do równania (6) zamiast p wyrażenie

(7)

gdzie: H - wysokość słupa danej cieczy równoważna spadkowi ciśnienia p (tzw. wysokość stracona),

g - przyspieszenie ziemskie,

otrzymano wyrażenie:

(8)

Wzór (8) będzie wykorzystany w dalszym ciągu ćwiczenia.

Współczynnik oporu  w rurach gładkich w zależności od Re można wyznaczyć dla różnych zakresów liczb Reynoldsa. Spośród wielu proponowanych w literaturze wzorów empirycznych najszersze zastosowanie do praktycznych obliczeń ma wzór Blasiusa (słuszny dla zakresu 2,3*10³<Re<3*10⁵):

  , Re ^-0,25 (9)

2. Współczynnik strat lokalnych.

W rurociągach spotykamy się jeszcze ponadto ze stratami energii powstałymi wskutek zmiany kierunku przepływu w kolankach, załamaniach i wskutek zmiany przekrojów poprzecznych przewodu jak np. przy gwałtownym rozszerzeniu lub zwężeniu przewodu, w dyfuzorach, konfuzorach, oraz wskutek występowania urządzeń dławiących przepływ jak np. zasuwy, przepustnice, zawory itp.

Tego rodzaju straty spowodowane przez przeszkody, znajdujące się na drodze przepływającego strumienia, nazywamy stratami miejscowymi lub lokalnymi. Straty te powodują spadek ciśnienia, który w postaci wysokości ciśnienia możemy określić dla przepływu turbulentnego jako

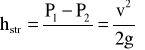
(10)

gdzie:

 - współczynnik strat lokalnych zależy od rodzaju miejscowej przeszkody i odniesiony jest najczęściej do średniej prędkości poza przeszkodą.

W dalszym ciągu rozważań dotyczących strat lokalnych będziemy zajmowali się ustaleniem wielkości, od których zależy współczynnik  oraz określeniem jego wartości liczbowych dla poszczególnych przeszkód lokalnych.

1. Zmiana kierunku przepływu.

Całkowite straty energii przy przepływie w kolanie możemy wyrazić jako:

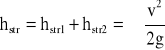
(11)

gdzie:

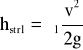
- straty na tarcie w kolanie

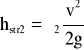
- straty spowodowane wytworzeniem poprzecznego wiru podwójnego i oderwaniem

stąd:

Współczynnik oporu całkowitego w kolanie o przekroju prostokątnym zależy od następujących parametrów:

(12)

gdzie:

 - kąt zmiany kierunku przepływu

R - promień zakrętu

b - szerokość przekroju

h/b - stosunek wymiarów przekroju poprzecznego

2. Zmiana przekroju poprzecznego

Rys.2. Przemiany energii przy gwałtownym rozszerzeniu przekroju poprzecznego

Gwałtowne rozszerzenie. Przy gwałtownym rozszerzeniu przekroju (rys.2) występują straty energii strumienia, które możemy określić za pomocą zasady ilości ruchu. Wydzielimy w tym celu myślowo obraz zawarty pomiędzy płaszczyznami 1- 1

i 2 - 2. Na powierzchnię (F₂ - F₁), działa jak wiadomo na podstawie doświadczenia, takie samo ciśnienie jak w przekroju F₁. Spowodowane jest to tym, że w miejscu rozszerzenia przewodu następuje oderwanie strumienia.

Stosując zasadę przyrostu ilości ruchu, otrzymamy:

(13)

gdzie:

ρ - gęstość płynącego czynnika (kg/m³)

Q - wydatek (m³/s)

v - prędkość czynnika (m/s)

p - ciśnienie (N/m²)

F - pole przekroju poprzecznego (m²)

a po uproszczeniach

ρQ(v₂ - v₁) = (p₁ - p₂)F₂ (14)

Podstawiając Q = F₂ v₂, otrzymamy:

ρ F₂v₂(v₂ - v₁) = (p₁ - p₂)F₂ (15)

skąd po skróceniu przez F₂ i po podzieleniu przez γ (ciężar właściwy cieczy) otrzymamy:

(16)

Obliczając różnicę ciśnień pomiędzy przekrojami 1-2 z równania Bernoulliego, otrzymamy:

(17) gdzie: h_str - straty ciśnienia wyrażone w metrach słupa cieczy.

Z porównania otrzymanych równań uzyskano:

(18)

skąd:

(19)

Otrzymany wzór (19) na obliczenie strat nosi nazwę wzoru Bordy-Carnota.

Uwzględniając równanie ciągłości v₁F₁ =v₂F₂ otrzymamy:

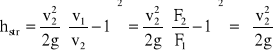
(20)

gdzie:

- współczynnik strat lokalnych :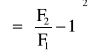

Można zauważyć, że długość drogi potrzebnej dla całkowitego rozszerzenia się strumienia wynosi: l = (8÷10)d₂ gdzie: d₂ - średnica przewodu rozszerzonego.

Rzeczywista strata energii przy gwałtownym rozszerzeniu jest nieco większa od obliczonej na podstawie wzoru Bordy-Carnota i dlatego zalecane jest wprowadzenie do tego wzoru współczynnika poprawkowego, określonego na podstawie doświadczeń.

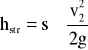
(21)

Dla rur o średnicy od 1,25 do 15 cm przy F₂/F₁ = 2÷12, współczynnik ten można obliczyć na podstawie następującego wzoru

, (22)

gdzie: d₁ - mniejsza średnica rury.

Gwałtowne zwężenie. Określenie strat energii strumienia przy gwałtownym zwężeniu (rys.3.) jest znacznie trudniejsze niż dla gwałtownego rozszerzenia. Podstawowe znaczenie mają tutaj straty występujące wskutek kontrakcji strumienia, a następnie wskutek gwałtownego rozszerzenia.

Opierając się więc na wzorze Bordy-Carnota możemy obliczyć straty z zależności:

(23)

Rys.3. Przemiana energii przy przepływie przez gwałtowne zwężenie.

Ponieważ współczynnik konstrukcji
(patrz rys.4) więc v₀  = v₂, a stąd:

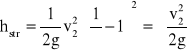
(24)

Zatem dla gwałtownego zwężenia: zależność współczynnika konstrukcji  wg Weisbacha podana jest na rys.4. Dla F₂  0,1F₁ wartość  oraz  podane są w poniższej tabeli

		UWAGI:
0,41÷0,314	0,61÷0,64	dla ostrych krawędzi
0,221÷0,0625	0,68÷0,8	dla małego załamania krawędzi
0,0125	0,9	dla małych zaokrągleń

Rys.4. Współczynnik konstrukcji  i współczynnik oporu  dla różnych stosunków przekrojów przy gwałtownym zwężeniu przewodu

Rys.5. Przemiany energii przy przepływie przez kryzę

Straty energii występujące przy gwałtownym zwężeniu są znacznie mniejsze niż straty przy gwałtownym rozszerzeniu.

Obliczając straty energii dla przepływu przez kryzę (rys.5.), podobnie jak w przypadku gwałtownego zwężenia przewodu otrzymamy:

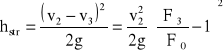
(25)

gdzie wg Weisbacha

(26)

Dla wlotów do przewodu (rys.6) współczynniki strat posiadają następujące wartości:

1. dla wlotu o ostrych krawędziach średnia wartość współczynnika  = 0,5, dla załamanych  = 0,25, a dla wlotów o dużych zaokrągleniach  = 0,1 ÷ 0,06;

2. dla wlotu zatopionego o ostrych krawędziach  =3,0 i o krawędziach zaokrąglonych  = 0,55;

3. dla wlotu pod kątem a o ostrych krawędziach:

 = 0,5+0,3sin+0,2sin²

Rys.6. Wloty do przewodu: a) o ostrych krawędziach b) zatopiony

c) skośny

Rys.7. Przemiany energii przy przepływie przez stopniowe rozszerzenie

przewodu

Stopniowe rozszerzenie przewodu. Współczynnik oporu  określający straty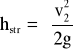
dla stożkowych rozszerzających się odcinków przewodu, czyli dla tzw. dyfuzorów (rys.7) zależy od kąta , od długości dyfuzora i od chropowatości ścianek przewodu.

1. dla krótkich dyfuzorów współczynnik  można określić ze wzoru dla

gwałtownego rozszerzenia, wprowadzając do niego współczynnik s:

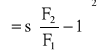
(27)

gdzie: s - przyjmujemy w zależności od kąta .

Wartości s =f() podane zostały w poniższej tabeli:\

^0	3	4	5	6	7	8	10	15	20	25
k	0,18	0,15	0,14	0,135	0,14	0,145	0,17	0,265	0,42	0,60

Dla kątów a < 25⁰ straty energii h_str dla dyfuzora są równe stratom dla gwałtownego rozszerzenia rury.

b) dla długich dyfuzorów należy uwzględniać straty na tarcie na długości dyfuzora oraz straty wywołane zmianą ilości ruchu. Straty na tarcie w dyfuzorze możemy obliczyć z następującej zależności, wyprowadzonej przez Fliegnera:

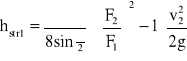
(28)

gdzie:  - przyjmujemy jako średnią wartość. Straty spowodowane zmianą ilości ruchu:

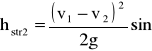
(29)

Całkowita strata energii przy przepływie przez dyfuzor

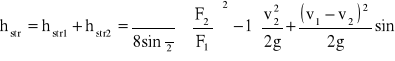
(30)

a stąd współczynnik

(31)

Określona z tego wzoru wartość  jest słuszna dla kątów  < 10°.

Stopniowe zwężenie przewodu. Przy przepływie przez stożkowe zwężające się odcinki przewodu, tzw. konfuzory (rys.8) występują tylko niewielkie straty energii wskutek tarcia na długości konfuzora, które można wyrazić w postaci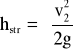

Rys.8. Przemiany energii przy przepływie przez stopniowe zwężenie przewodu.

Na podstawie obliczeń Fliegnera:

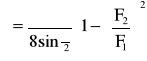
(32)

Praktycznie przyjmujemy dla małych kątów zbieżność ( = 5⁰)  = 0,005+0,06

w zależności od płynności przejścia. Dla kątów  < 15⁰ możemy przyjmować  = 0,1.

1. . Urządzenia dławiące przepływ.

Do urządzeń dławiących przepływ będziemy zaliczali zasuwy, przepustnice, zawory itp. Dokładne obliczenie strat dla przepływu przez te urządzenia napotyka duże trudności. Dlatego też najczęściej straty energii dla tych urządzeń wyznaczane są przez określenie wartości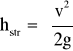
w drodze doświadczalnej. Współczynniki  odniesione są tutaj do prędkości za przeszkodą.

Zasuwa. Przy przepływie przez zasuwę (rys.9) wartość współczynnika  zależy od stosunku h/d, tj. od stopnia otwarcia zasuwy.

Rys.9. Zasuwa

Wartości liczbowe współczynnika  podane zostały dla zasuwy w poniższej tabeli:

h/d
	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0

Kształt okrągły	97,8	35,0	10,0	4,6	2,1	1,0	0,45	0,17	0,06	0
Kształt kwadratowy	103	44,5	17,8	0,1	4,0	2,1	0,95	0,40	0,09	0

Przepustnice. Współczynnik  dla przepływu przez przepustnicę (rys.10) zależy od otwarcia przepustnicy, które określa się za pomocą kąta .

Wartości liczbowe współczynnika  = f(⁰) podane zostały w tabeli:

^0	0	5	10	15	20	30	40	50	60	70	90
	0,05	0,24	0,52	0,90	1,54	3,91	10,8	92,6	118	700	?

Rys.10. Przepustnica

Rys.11. Kurek

Kurek. Współczynnik oporu  dla przepływu przez kurek (rys.11) zależy od stopnia jego otwarcia określonego kątem . Wartości  podane zostały poniżej:

^0	5	10	15	20	25	30	35	40	45	50	55
	0,05	0,29	0,75	1,56	3,10	5,47	9,68	17,3	31,2	52,6	106

Zawory. Współczynniki  przyjmujemy w zależności od konstrukcji zaworu, np. dla pełnego otwarcia zaworu podanego na rys.11a przyjmujemy  = 3÷5,5, a dla zaworu przedstawionego na rys.11b  = 1,4÷1,85. Dla smoka podanego na rys.12 z zaworem zwrotnym przyjmujemy  = 10, a dla smoka bez zaworu zwrotnego  = 5÷6.

Rys.12. Rodzaje zaworów:

1. prosty

2. skośny

Rys.13. Smok z zaworem

zwrotnym

OPIS INSTALACJI POMIAROWEJ I WYKONANIE ĆWICZENIA

Stanowisko pomiarowe (rys.14) składa się z następujących elementów:

1. zbiornika dolnego (A)

2. wodomierza do pomiaru wydatku (W)

3. rury łączącej zbiornik dolny ze zbiornikiem górnym (D)

4. pompy (P)

5. zaworu (F)

6. rury przelewowej (G)

7. zaworów (H, I, J) łączących zbiornik górny z rurociągami L ,O i S.

8. rurek piezometrycznych, których miejscem podłączenia są punkty pomiarowe oznaczone literami h

9. zaworu badanego (K)

10. zbiornika górnego (B)

11. wyposażenie dodatkowe: stoper, taśma miernicza, termometr, suwmiarka.

Woda w układzie płynie w obiegu zamkniętym. Zasysana jest ze zbiornika (A) poprzez przewód (D), pompę (P), zawór (F) - a następnie przetłaczana do zbiornika górnego (B), skąd możliwy jest spływ grawitacyjny przez każdy z trzech przewodów pomiarowych poprzez otwarcie zaworu H, I lub J. Przepływ przez przewód (L) umożliwia przeprowadzenie badań i obliczeń współczynnika strat na długości . Pomiary „na przewodzie” (O) pozwalają na określenie strat lokalnych dla przypadku wypływu z rury o większej średnicy do rury o mniejszej średnicy i na odwrót. Wreszcie pomiary „na przewodzie” (S) pozwalają na badanie i obliczenie strat lokalnych na zaworze (K).

Zawór (M) na końcu zbieracza (N) łączącego trzy przewody pozwala na dławienie przepływu odpowiednio w przewodach (L, O i S) a co za tym idzie prowadzenie badań dla różnych liczb Reynoldsa. Podczas pomiarów, rura przelewowa (G) zapewnia utrzymanie stałego poziomu wody w zbiorniku górnym (B).

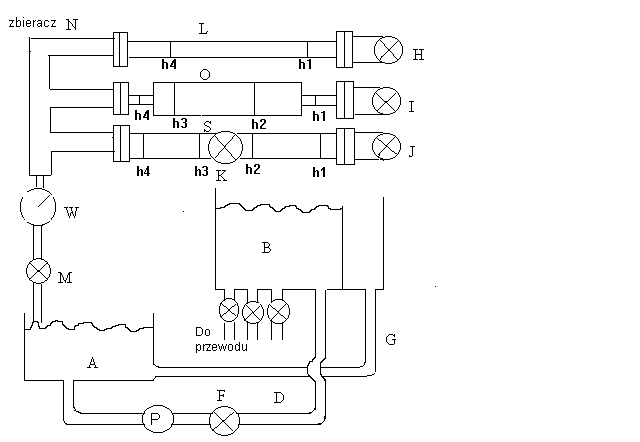
Rys.14. Schemat stanowiska pomiarowego

Wykonanie pomiarów odbywa się w następującej kolejności:

1. Ustalić przepływ wody w układzie poprzez włączenie pompy i odkręcenie zaworu (F) przy otwartym jednym z zaworów H, I lub J ( w zależności od tego który przewód badamy). Należy je otwierać ostrożnie, aby nie zapowietrzyć piezometrów lub nie spowodować wylewania z nich wody.

2. Odczytać wysokości słupów wody w rurkach piezometrycznych;

3. Zmierzyć i zapisać czas t, w którym przez wodomierz W przepłynie określona objętość wody.

4. Zmienić natężenie przepływu przy pomocy zaworu M. Zmiany natężenia przepływu dokonywać ostrożnie z powodów tak jak w punkcie 2;

5. Powtórzyć pomiary z punktu 4÷6;

6. Wyniki zanotować w tabelach pomiarowych;

7. Badania z punktów 1÷8 należy przeprowadzić dla przewodów wskazanych przez prowadzącego ćwiczenie;

Uwaga: Po zakończeniu badań należy:

1. Zamknąć zawory H, I i J;

2. Zamknąć zawór F

3. Wyłączyć pompę

4. Doprowadzić do czystości stanowisko pomiarowe

Instrukcja i wykonanie:

Wyznaczenie współczynnika strat lokalnych i na długości.

Piezometryczna linia ciśnień.

Tablica pomiarowa (taka sama przy badaniu strat na długości i strat lokalnych):

L.p.	V [dm^6]	t [s]	h1 [mm H2O]	h2 [mm H2O]	h3^* [mm H2O]	h4^* [mm H2O]

^* - niepotrzebne skreślić.

Tablice wynikowe:

a) straty na długości

L.p.	Q [m^3/s]	ΔHśr [m H2O]	vśr [m/s]	λ [-]	Re [-]	λt [-]

Dane geometryczne:

d = 0,013 m - średnica rury gładkiej

l = 3,2 m - odległość pomiędzy punktami pomiarowymi na rurze gładkiej

ν = 1,06 ·10^-6 [m²/s]

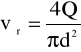
Obliczenia:

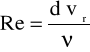
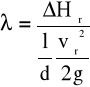
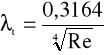
b) straty lokalne na przewężeniach przewodu

L.p.	Q [m^3/s]	v1 [m/s]	v2 [m/s]	ΔH1 [m H2O]	ΔH2 [m H2O]	ΔH3 [m H2O]	ξ1 [-]	ξ2 [-]

Dane geometryczne:

d₁ = 0,013 m - średnica węższej części przewodu,

d₂ = 0,020 m - średnica szerszej części przewodu,

l₁ = 0,52 m - odległość pomiędzy punktami pomiarowymi h₁ i h₂ lub h₃ i h₄,

l₂ = 1,52 m - odległość pomiędzy punktami pomiarowymi h₂ i h₃,

l₃ = 0,26 m - odległość pomiędzy przekrojem rozszerzenia przewodu a punktem pomiarowym

h₁ lub przekrojem zwężenia a punktem pomiarowym h₄.

Obliczenia:

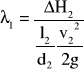
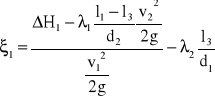
- współczynnik oporu rozszerzenia

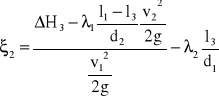
- współczynnik oporu zwężenia

Uwaga: Wartość współczynnika λ₂ należy przyjąć na podstawie punktu a) dla odpowiedniej

wartości wydatku Q.

c) straty lokalne na zaworze

L.p.	Q [m^3/s]	vśr [m/s]	ΔHśr [m H2O]	Re [-]	ξ [-]

Dane geometryczne:

d = 0,013 m - średnica rury gładkiej

a = 0,80 m - odległość pomiędzy punktami pomiarowymi

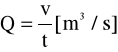
Obliczenia:

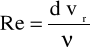
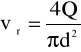
Sprawozdanie:

W sprawozdaniu należy zamieścić wykonane na papierze z naniesioną skalą logarytmiczną

następujące wykresy: λ=f(Re), λ_t=f(Re) i ξ=f(Re).

Przykładowe pytania kontrolne

1. Wymień i omów podstawowe rodzaje strat ciśnienia w przewodach hydraulicznych

2. Jakie czynniki wpływają na wartość współczynnika strat na długości ?

3. Omówić wykres Nikuradsego ?

4. Podaj znane Ci sposoby wyznaczania współczynnika strat lokalnych.

5. Omówić wpływ liczby Reynoldsa na współczynnik strat liniowych.

6. Wymienić i krótko omówić najczęściej spotykane elementy osprzętu hydraulicznego powodujące powstawanie strat lokalnych w przewodzie.

7. Jakie parametry są mierzone podczas wykonywania *wiczenia i jakimi metodami ?

SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ
KATEDRA TECHNIKI POŻARNICZEJ			LABORATORIUM HYDROMECHANIKI
Ćwiczenie nr:	5	Pluton: Grupa:	Imię i nazwisko		Ocena
Temat: STRATY LOKALNE I NA DŁUGOŚCIACH W RURACH GŁADKICH
Prowadzący:			Data wykonania:	Data złożenia:

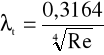
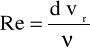
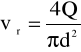
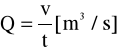
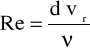
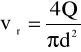
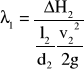
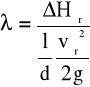
LABORATORIUM HYDROMECHANIKI

ĆWICZENIE NR 5

Temat: Straty lokalne i na długości w rurach gładkich

Edycja 2

Strona 23

Ilość stron 18

Data: 02-09-25

---