WYKŁAD 2

Układy złożone z elementów biernych

Bierne elementy elektroniczne to :

opór R:

indukcyjność L:

i pojemność C:

Rozważmy obwód złożony z tych elementów połączonych szeregowo, zasilany ze źródła napięciowego o zmiennej sile elektromotorycznej reprezentowanej przez część rzeczywistą wyrażenia: u(t)=U₀e^jωt, gdzie U₀ oznacza amplitudę napięcia, a ω=2πν - częstotliwość kołową . Natężenie prądu płynącego przez układ ma podobną postać: i(t)=I₀e^jωt.

Skorzystamy z drugiego prawa Kirchhoffa :

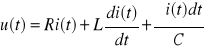
Podstawiając powyższe postaci natężenia oraz napięcia i dzieląc stronami przez I₀ otrzymujemy:

Wielkość Z jest impedancją powyższego obwodu i jest wielkością zespoloną. Możemy w niej wyróżnić impedancje poszczególnych elementów: oporu: Z_R=R, indukcyjności: Z_L=jωL oraz pojemności: Z_C=1/jωC. Dokonaliśmy w ten sposób uogólnienia prawa Ohma dla prądów zmiennych: napięcie u(t) jest liniowym funkcjonałem prądu i(t). Nadal obowiązują prawa Kirchhoffa. W ogólności dla innych obwodów postać algebraiczna impedancji może być inną liczbą zespoloną. W powyższym przypadku, przy szeregowym połączeniu impedancji uzyskujemy wzór na impedancję wypadkową : Z_W= Z₁+Z₂+...+Z_n , analogiczny jak przy łączeniu oporów. Przy równoległym połączeniu impedancji : 1/Z_W=1/Z₁+1/Z₂+...+1/Z_n.

Część rzeczywistą impedancji nazywa się rezystancją, część urojoną - reaktancją. Stosunek reaktancji do rezystancji jest równy tangensowi kąta przesunięcia fazowego ϕ między napięciem i natężeniem.

Reprezentacja impedancji na płaszczyźnie zespolonej :

Rezystancja opisuje zdolność obwodu do zamiany energii elektrycznej na ciepło:, natomiast pojemność i indukcyjność - zdolność do magazynowania energii elektrycznej, odpowiednio: - w polu elektrycznym pojemności oraz w polu magnetycznym indukcyjności.

Należy pamiętać, że opór, indukcyjność i pojemność to pojęcia teoretyczne. Rzeczywiste konstrukcje, jak opornik, cewka czy kondensator zawierają wielkości pasożytnicze oznaczone na rysunku poniżej indeksem p:

- a więc są złożonymi impedancjami. Przy pewnych częstotliwościach sygnału wielkości pasożytnicze mogą istotnie zniekształcić własności danego elementu.

Obwód drgający

Rozważmy obwód złożony z szeregowo połączonych: indukcyjności, pojemności i oporu. Kondensator został naładowany do napięcia U_C0, po czym zamknięto wyłącznik. Ruch ładunku w obwodzie opisuje równanie :

,

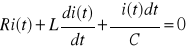
które łatwo można przekształcić w liniowe równanie różniczkowe drugiego stopnia :

.

Zakładamy, że rozwiązanie ma postać wykładniczą : . Podstawiając je do powyższego równania różniczkowego otrzymujemy równanie algebraiczne: , którego pierwiastki mają wartość: oraz . Rozwiązanie równania ruchu ładunku w obwodzie jest kombinacją liniową rozwiązań z α₁ i α₂ :

,

przy czym wartości amplitud A₁ i A₂ możemy wyznaczyć z warunków początkowych :

,

Przypadki :

• Jeżeli , wtedy jest liczbą rzeczywistą i rozwiązania mają charakter dwuwykładniczy :
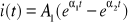
  , a więc po wzbudzeniu prąd w obwodzie zanika.

• Gdy , wtedy jest liczbą urojoną i rozwiązania mają charakter oscylacyjny :
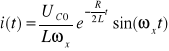
  , gdzie częstotliwość oscylacji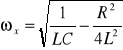
  .

• W szczególnym przypadku, gdy R=0 otrzymujemy drgania niegasnące [] : , gdzie częstotliwość oscylacji : .

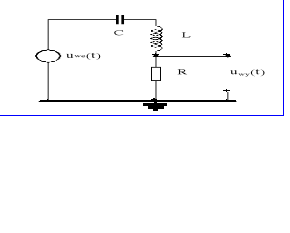
Filtr rezonansowy szeregowy.

Obecnie będziemy analizowali pracę szeregowego układu RLC, do którego dołączono napięciowe źródło sygnału przemiennego o częstotliwości ω. Ze wzoru na dzielnik napięcia otrzymujemy napięcie na poszczególnych elementach :

, ,

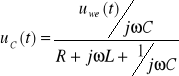
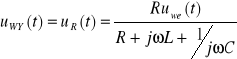
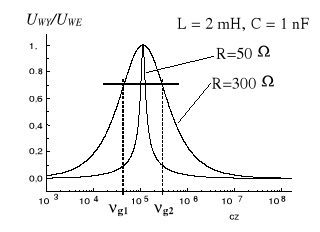
Stosunek amplitud napięcia wyjściowego do wejściowego (tzw. transmitancja układu) wynosi: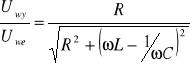
,

a przesunięcie fazowe między sygnałem wejściowym i wyjściowym :

Układ ten nazywany jest filtrem rezonansowym szeregowym. Pasmo jego przepuszczania zlokalizowane jest w okolicach częstotliwości .

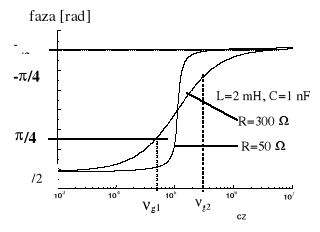
Pasmo przenoszenia filtru rozciąga się od ν_g1 do ν_g2,, nazywanych częstościami granicznymi. Dla częstości granicznych zachodzi równość :

, oraz : .

Dla częstotliwości moduły napięć na poszczególnych elementach obwodu mają odpowiednio wartości :

, , U_R=U₀.

a impedancja obwodu wynosi R. Dla tej częstotliwości znika łączna impedancja elementów reaktancyjnych, a napięcia na kondensatorze i indukcyjności osiągają wartości maksymalne. Zjawisko to nosi nazwę rezonansu, a ω₀ to częstotliwość rezonansowa. W rezonansie amplitudy napięcia na indukcyjności lub na pojemności mogą przekroczyć amplitudę napięcia wejściowego. Wielkość: ,

nazywana jest dobrocią obwodu . Inna postać dobroci :

Ogólna definicja : Dobroć wyraża stosunek energii zmagazynowanej w układzie rezonansowym (E_L) do mocy traconej w nim (P) w ciągu jednego okresu drgań (T).

Magazynowanie energii w elementach reaktancyjnych obwodu rezonansowego o wysokiej dobroci i wywołane przez nie „podbijanie” napięcia jest wykorzystywane do filtracji i transformowania sygnałów o określonej częstotliwości.

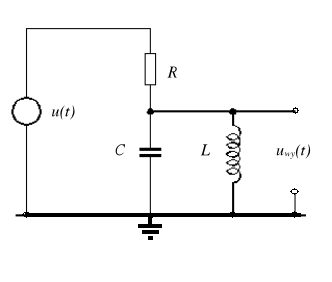
Filtr rezonansowy równoległy :

Dla częstotliwości rezonansowej napięcie wyjściowe osiąga wartość minimalną.

.

Pracownia WstĘpna

Instrukcja do ćwiczenia nr.2 pt. „Układ oscylujący”

1. Cel ćwiczenia.

• Zaznajomienie się z oscyloskopem i generatorem.

• Zbadanie własności układu oscylującego RLC

2. Wymagania :

• Materiał z poprzednich wykładów i ćwiczeń.

• Biegła umiejętność rozwiązywania obwodów z elementami RLC.

• Znajomość przepływu prądu przez układ oscylujący.

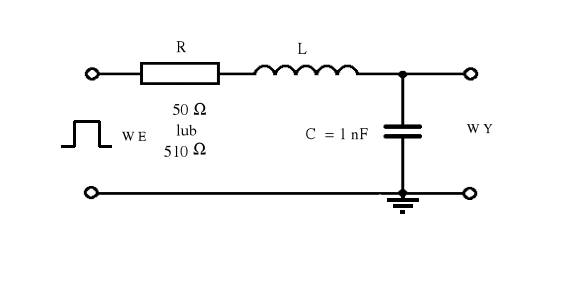
3. Wykonanie ćwiczenia.

• Zmontować na płytce obwód drgający według podanego obok schematu. W pierwszej kolejności do budowy układu użyć opornika o wartości 50 Ω.

• Zbudować układ pomiarowy podłączając na wejście obwodu drgającego generator, Wyjścia obwodu drgającego łączymy z kanałem B oscyloskopu. Sygnał z wyjścia generatora poprzez trójnik należy doprowadzić do kanału A oscyloskopu. Podstawa czasu oscyloskopu powinna być wyzwalana w sposób zewnętrzny, z dodatkowych wyjść generatora.

• Na wejście obwodu podać z generatora sygnał prostokątny o maksymalnej amplitudzie i o częstotliwości 1 kHz. Zbocza narastające i opadające tego sygnału pobudzają w obwodzie drgania gasnące.

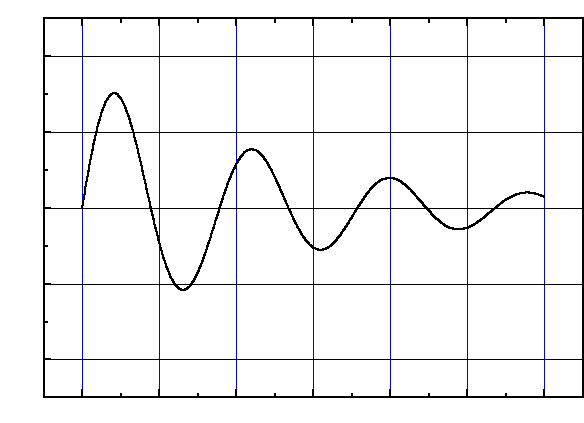
• Dokonać pomiaru kształtu pojedynczego ciągu oscylacji, szczególnie starannie rejestrując jego maksima i minima oraz przejścia przez zero. Należy pamiętać o zmienianiu czułości i podstawy czasu oscyloskopu tak, by osiągnąć jak największą dokładność. W czasie pomiaru umieścić obwód rezonansowy zdala od innych przedmiotów i nie przybliżać do niego rąk, by nie zakłócić jego parametrów pasożytniczym wpływem otoczenia.

• Wymienić w układzie opornik na 510 Ω i dokonać powtórnego pomiaru przebiegu prądu.

• Do zarejestrowanych przebiegów dopasować funkcję U₀e^-atcos(ωt). Nanieść tę funkcję na punkty doświadczalne. Na podstawie podanych na wykładzie wzorów na a i ω wyznaczyć indukcyjność obwodu. Dla poprawnej interpretacji wyników należy uwzględnić rezystancję wyjściową generatora (50 Ω). Czy pojemności kabli i rezystancja wejściowa oscyloskopu mają istotny wpływ na pracę obwodu oscylującego ? Czym wyjaśnić rozbieżności wartości L otrzymane dla R=50 Ω i R= 510 Ω ?

Dodatek 4. Dopasowanie funkcji U₀e^-atcos (ωt) do danych doświadczalnych.

• Miejsca zerowe szukanej funkcji wyznaczone są przez miejsca zerowe funkcji cosinus. Okres tej funkcji (a dzięki temu i częstotliwość ω) znajdujemy więc jako podwojoną średnią arytmetyczną z odległości czasowych miedzy kolejnymi miejscami zerowymi.

• Tworzymy pomocniczy wykres (współrzędne : czas - napięcie, oś napięciowa - logarytmiczna) dla bezwzględnych wartości zarejestrowanych maksimów i minimów. Punkty doświadczalne ułożą się wzdłuż prostej : ln(U) = -a(t-t₀) + lnU₀ . Należy dopasować tę prostą do punktów doświadczalnych, znajdując współczynnik nachylenia a (a tym samym współczynnik tłumienia dla funkcji wykładniczej) oraz amplitudę U_0.

.Dodatek 5. Opisy.

Podstawą pozytywnej oceny pracy doświadczalnej jest rzetelne przeprowadzenie eksperymentu, ale praca może być dobrze oceniona tylko wtedy, gdy jej wyniki zostaną poprawnie opisane. Właściwe przedstawianie rezultatów swej pracy jest sztuką, której warto się uczyć.

Opis doświadczenia z pracowni studenckiej powinien być zwięzły i zawierać tylko niezbędne informacje. Nie ocenia się narzędzia, którym się posłużono (rachunek ręczny, suwak logarytmiczny, kalkulator, maszyna do pisania, komputer), ale stronę merytoryczną i formę opisu, który musi być czytelny.

W zasadzie opis powinien składać się z trzech części :

• wstępu, w którym wyjaśnia się cel doświadczenia. Nie należy tracić miejsca na podawanie historii zjawisk i życiorysów odkrywców, ani przepisywać z podręczników partii materiałów z opisami zjawiska.

• rozwinięcia, który zawiera przebieg doświadczenia , jego schemat, wyjaśnienia co do przebiegu pomiaru, wyniki i ich dyskusję a także wnioski,

• zakończenia, będącego jednocześnie podsumowaniem, zawierającym wnioski ogólne.

Bardzo ważna jest komunikatywność opisów - informacje powinny być przedstawione w taki sposób, by były dobrze i jednoznacznie zrozumiałe dla czytającego. Poza poprawnym językiem należy posłużyć się poprawną formą przedstawienia rezultatów. Wszystkie rysunki powinny być ponumerowane i podpisane. Ideałem jest włączanie (choćby przez wklejanie) rysunku do odnoszącego się do niego tekstu.

W czasie pomiarów dane są zwykle zapisywane w postaci tabeli, jednak, poza wyjątkowymi przypadkami (takim przypadkiem jest ćwiczenie I z Pracowni Wstępnej), w opisie powinny się one znaleźć w postaci wykresu. Tabele pomiarowe można dołączyć jako dodatek do opisu na jego końcu.

3 4 5 6 - błąd

Wykres spełni swoją rolę, jeżeli będzie starannie opracowany. Należy zastanowić się, czy zastosujemy na osiach skalę logarytmiczną, czy liniową, czy jakąkolwiek inną. Oś powinna być opisana, posiadać jasno zaznaczoną podziałkę i podane jednostki. Przy wyborze skali logarytmicznej (w skali ogólności nieliniowej) zaznaczamy na skali nie logarytmy wartości, ale ich rzeczywiste wielkości. Punkty doświadczalne powinny być reprezentowane za pomocą odpowiednich symboli; powinny być zaznaczone niepewności ich wartości wyliczone w oparciu o rzetelny rachunek błędów. Jeżeli na tym samym rysunku przedstawiamy różne serie pomiarowe, stosujemy różne symbole.

Jeżeli badane zjawisko posiada swój opis teoretyczny którego wynikiem jest konkretna funkcja (jak w przypadku rezonansu) należy dopasować krzywą teoretyczną do danych doświadczalnych i sprawdzić, czy parametry dopasowania potwierdzają zgodność teorii z doświadczeniem w granicach błędu eksperymentalnego. Na osiach zaznaczmy charakterystyczne wielkości krzywej teoretycznej. Niedopuszczalne jest łączenie punktów doświadczalnych prostą łamaną. Błędem jest także ciągnięcie krzywej przez punkty doświadczalne przy pomocy krzywika. Krzywikiem można się posłużyć aproksymując krzywą teoretyczną, ale wpierw należy zaznaczyć kilka punktów teoretycznych. Wszystkie rysunki powinny być ponumerowane i podpisane. Dobrze jest włączać rysunki (choćby przez wklejanie) do odnoszącego się do nich tekstu.

Rysunek nie jest dodatkiem do tekstu, gdyż często dostarcza więcej informacji niż wielostronicowy opis. Nie zwalnia to jednak autora pracy z konieczności przedyskutowania rysunku w opisie.

Opracowując wyniki doświadczenia prezentujemy zwykle kilka tez. Należy jednoznacznie wskazać w opisie fakt potwierdzający daną tezę.

Dodatek 6. Oscyloskop.

Oscyloskop jest uniwersalnym urządzeniem pomiarowym służącym do badania i wizualizacji zmiennych przebiegów elektrycznych.

OSCYLOSKOP JEDNOKANAŁOWY- uproszczony schemat blokowy

Sygnał generatora podstawy czasu

Sposoby wyzwalania podstawy czasu

Uproszczony schemat oscyloskopu dwukanałowego

Tutaj oznacza jednostkę urojoną, w odróżnieniu od prądu i.

Skorzystaliśmy tutaj z tożsamości :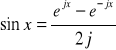
.

[] Ponieważ w rzeczywistym obwodzie zawsze występuje dodatnia rezystancja (np. pasożytnicza), aby uzyskać R=0 do obwodu należy wprowadzić rezystancję ujemną, którą jest np. wzmacniacz albo inny odpowiedni element elektroniczny.

Wykazać (to co widać na rysunkach na poprzedniej stronie), że Q=ω₀/Δω, gdzie Δω jest szerokością połówkową charakterystyki układu rezonansowego, czyli funkcji f(ω)=|u_C(ω,t)/u(ω,t)|.

t₀ jest czasem wystąpienia pierwszego ekstremum po momencie wzbudzenia oscylacji.

12

---