STATYSTYKA

1. Podstawowe pojęcia

ZMIENNA - wszelka własność, która może występować w różnym stopniu i pod względem której ludzie różnią się między sobą lub zmieniają w czasie

• jakościowa np. płeć, zawód - można za nią podstawiać wyłącznie nazwy, na ogół ma charakter nieciągły

• ilościowa np. wiek, iloraz inteligencji - jej zakresem jest zbiór liczb, ma ciągły charakter

• stała np. Л - jej zakres stanowi klasa zawierająca jeden element

• dyskretna np. płeć, liczba dzieci w rodzinie - pomiędzy dwie sąsiednie wartości zmiennej nie można wstawić trzeciej

• ciągła np. wzrost - pomiędzy dwie sąsiednie wartości zmiennej można wstawić trzecią, jej zbiór wartości tworzy kontinuum

ZAKRES ZMIENNEJ - zbiór wartości zmiennej

POMIAR - przyporządkowanie liczb przedmiotom zgodnie z określonymi regułami, w taki sposób, aby liczby odzwierciedlały zachodzące między tymi przedmiotami stosunki

• podstawowy np. pomiar długości - ilość mierzonej własności określa się przez proste i bezpośrednie porównanie z przedmiotem, który posiada pewną standardową ilość tej własności; własności mierzone z pomocą tego pomiaru to własności ekstensywne

• pochodny np. pomiar temperatury - wymaga posługiwania się logicznymi lub matematycznymi prawami dotyczącymi miar podstawowych; własności mierzone za pomocą tego pomiaru to własności intensywne

• bezpośredni np. pomiar długości

• pośredni np. pomiar gęstości

• wskaźnikowy np. ważenie - polega na przyporządkowaniu liczb przedmiotom na podstawie bezpośredniego odczytu na skali jakiegoś przyrządu

• 
  umowny np. pomiar inteligencji za pomocą testu - opiera się na związku między obserwacją a mierzoną zmienną

SKALOWANIE - polega na konstrukcji skal pomiarowych o określonych własnościach

skala	nominalna (nazwowa)	porządkowa (rangowa)	przedziałowa (interwałowa)	stosunkowa (ilorazowa)
Możemy stwierdzić, że…	coś jest równe lub różne	coś jest mniejsze lub większe	coś jest mniejsze lub większe o tyle a tyle	coś jest mniejsze lub większe tyle a tyle razy
Posiada…	kategorię	kategorię, kontinuum	kategorię, kontinuum, jednostkę	kategorię, kontinuum jednostkę, moment zaniku
Mierzymy…	płeć, zawód	twardość minerałów	temperaturę	długość, masę, czas reakcji

KATEGORYZACJA musi być wyczerpująca i rozłączna

POPULACJA - zbiorowość generalna - zbiór elementów zróżnicowanych ze względu na pewną cechę ilościową lub jakościową opisywany metodami statystycznymi, o którego własnościach wnioskuje się na podstawie pewnej jego reprezentacji (próby)

PRÓBA - jest to dowolna podgrupa lub podzespół wybrany z populacji za

pomocą odpowiedniej metody; musi być reprezentatywna tzn

odzwierciedlać to co zachodzi na poziomie populacji oraz losowa

2. Miary i ich własności

I. Miary centrum

PRÓBA	POPULACJA
m - modalna - wartość x najczęściej występująca w próbie (fi - fi-1) ⋅ h m = xid + -------------------- (fi - fi-1)+(fi - fi+1)	M - modalna - wartość x najbardziej prawdopodobna
me - mediana - środkowa wartość zmiennej (½n - fci-1) ⋅ h me = xdi + --------------------- fi	Me - mediana - wartość X poniżej której wartości zmiennej realizują się z pewnością 0.5 i powyżej której wartości zmiennej realizują się z pewnością 0.5
- średnia arytmetyczna - przeciętna wartość zmiennej xi x1 + x2 +…+ xn = ------- = --------------------- n n	µ (mi) - wartość oczekiwana

Własności miar centrum:

modalna:

• jest bardzo zależna od rozpiętości (h)

mediana:

• jest niezależna od wielkości skrajnych

• suma bezwzględnych odchyleń wszystkich wartości pomiarowych Xi od ich mediany jest mniejsza od odchyleń tych pomiarów od jakiejkolwiek innej wartości
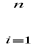
  |xi - me| <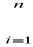
  |xi - xo|

średnia arytmetyczna:

• jest punktem równowagi odległości wszystkich pomiarów mniejszych i większych od średniej
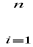
  (xi -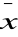
  ) = 0

• jest bardzo zależna od wartości skrajnych

• suma kwadratów wszystkich odchyleń wielkości pomiarowych od ich wielkości średniej jest mniejsza od sumy kwadratów odchyleń tych pomiarów od każdej dowolnej wielkości pomiarowej
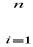
  (xi -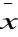
  )² <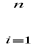
  (xi - xo)²

II. Miary rozproszenia

PRÓBA	POPULACJA
v - rozstęp - różnica między największym i najmniejszym pomiarem v = xmax - xmin 7 ↑ v ≈ 6•s (rozkład o idealnym kształcie) ↓ 5	v - odcinek wartości skali X, dla których prawdopodobieństwa są różne od 0
s² - wariancja - przeciętna kwadratowa odległość pomiarów od średniej arytmetycznej (xi - )² (xi - )²⋅ fi s² = -------------- = ----------------- n-1 n-1	σ² - wariancja nie obowiązuje
s - odchylenie standardowe - przeciętna odległość pomiarów od średniej arytmetycznej s =	σ (sigma)- odchylenie standardowe

Własności miar rozproszenia:

• Jeżeli do wszystkich pomiarów xi zmiennej x doda się taką samą stałą c, to odchylenie standardowe zmiennej x +c pozostanie niezmienione: sx = sx+c

• Jeżeli wszystkie pomiary xi zmiennej x zostaną pomnożone przez pewną taką samą wartość stałą c, to odchylenie standardowe zmiennej c zostanie zwiększone o |c| względem odchyleń x: sx ⋅c = |c| ⋅ sx

• 
  
  Uśredniona suma kwadratów różnic między parą pomiarów równa jest podwojonej wariancji

III. Miary skośności

• IV.

3. Standaryzacja - uwalnianie zmiennych od ich jednostek i sprowadzanie ich do wspólnego mianownika; jest transformacją wyników, która pozwala na ich porównywanie; jednostką wyników wystandaryzowanych jest odchylenie standardowe

- wynik surowy zmiennej x

-

- wynik standaryzowany zmiennej x
= ------------

s

4. Aby scharakteryzować rozkład należy:

• narysować wykres

• uciąglić zmienną, obliczyć rozpiętość klasy (h), frekwencję skumulowaną (fc), proporcję (p), czyli frakcję

• obliczyć miary tendencji centralnej (modalną, medianę, średnią arytmetyczną)

• obliczyć miary rozproszenia (rozstęp, wariancję, odchylenie standardowe)

• obliczyć pierwszą miarę skośności - określić czy rozkład jest lewoskośny, prawoskośny czy symetryczny

• określić czy rozkład jest leptokurtyczny, platykurtyczny czy normalny

Liczba stopni swobody dla statystyki będącej estymatorem nieznanej wartości parametru populacji jest równa liczbie wyników, które w niezależny sposób przyczyniają się do wyznaczenia wartości tej statystyki. Jednemu wynikowi zabieramy możliwość dowolnego zrealizowania się dla niego zmiennej, ponieważ musimy dopasować go do pozostałych wyników, ponieważ traktujemy średnią jako stałą charakterystykę próby.

xi	fi	fci	p
5 - 9	1	1	0.01
10 - 14	10	11	0.10
15 - 19	37	48	0.37
20 - 24	36	84	0.36
25 - 29	13	97	0.13
30 - 34	2	99	0.02
35 - 39	1	100	0.01
	n= 100

k = 7 liczba klas hi = xgi - xdi rozpiętość klasy

p =
proporcja

(37 - 10) ⋅ 5 27 ⋅ 5

m = 14.5 + ---------------------------- = 14.5 + ----------- = 19.32

(37 - 10) + (37 - 36) 27 + 1

(50 - 48) ⋅ 5 10

me = 19.5 + ------------------ = 19.5 + ------ = 19.78

36 36

(7 ⋅1) + (12 ⋅ 10) + (17 ⋅ 37) + (22 ⋅ 36) + (27 ⋅ 13) + (32 ⋅ 2) + (37 ⋅ 1) 2000

= ---------------------------------------------------------------------------------------- = ------ = 20

100 100

v = 39.5 - 4.5 = 35

(7-20)˛⋅1 + (12-20)˛⋅ 10 + (17-20)˛⋅ 37+ (22-20)˛⋅ 36+ (27-20)˛⋅ 13+ (32-20)˛⋅ 2+ (37-20)˛⋅ 1

s˛ = -------------------------------------------------------------------------------------------------------------------=

100 - 1

2500

= -------- = 25.25 s = 25.25 ≈ 5.025

99

3(20 - 18.78) 0.66

k = ------------------- = -------- ≈ 0.13 k > 0 rozkład jest odrobinkę prawoskośny

5.025 5.025

v = ? ⋅ s

35 = ?⋅ 5.025 rozkład jest leptokurtyczny

↓

1. (Im więcej niż 6, tym rozkład jest bardziej leptokutyczny.)

5. Rozkład normalny i jego własności

Rozkład normalny:

jest rozkładem teoretycznym - modelem jest rozkładem zmiennej ciągłej przyjmującej wartości od -∞ do +∞ jest krzywą wypukłą jest symetryczny : µ = Me =M jego postać determinuje średnia arytmetyczna i wariancja X→ N(µ, σ²) Wszystkie rozkłady normalne tworzą klasę rozkładów normalnych. Pole pod krzywą dla całej osi = 1.

6. Własności standaryzacji

• x = 0

• s = 1, s² = 1

• nie zmienia rozkładu zmiennej dyskretnej, ale zmienia rozkład zmiennej ciągłej

σ < 1 rozkład bardziej spłaszczony

σ > 1 rozkład jest bardziej smukły

σ = 1 rozkład jest taki sam

• zachowuje pole pod krzywą

P(x1 ≤ X ≤ x2) = F(x2) - F (x1) = Φ(Z1) - Φ(Z2)

7. Wystandaryzowany rozkład normalny i jego własności

8. Centralne twierdzenie graniczne (twierdzenie LINDEBERGA - LÉVÝEGO) i wnioski z niego wynikające

Jeżeli z populacji, w której zmienna losowa ma dowolny rozkład prawdopodobieństwa ze średnią równą µ i wariancją równą σ² losujemy kolejno próby o coraz większych rozmiarach (n→ ∞), to w miarę wzrostu liczby losowań (l→ ∞) rozkład estymatora µ, czyli średniej z próby dąży do rozkładu normalnego ze średnią równą µ i wariancją równą σ²/n (oraz odchyleniem standardowym równym σ/
) .

Nie wszystkie statystyki z próby to estymatory!!!

Błędem standardowym nazywamy odchylenie standardowe w rozkładzie statystyki z próby.

Im większe próby, tym mniejsze odchylenie standardowe, czyli mniejszy błąd standardowy.

9. Dystrybuanta

• Dystrybuantą zmiennej losowej X nazywamy funkcję określoną wzorem F(x) = P(X ≤ x).

• Dystrybuanta w punkcie x to prawdopodobieństwo, że zmienna losowa przyjmie wartości mniejsze, bądź

równe x.

• Estymatorem dystrybuanty w próbie dla xi są frekwencje skumulowane podzielone przez liczbę elementów próby fc/n.

10.

• Jakie ilorazy inteligencji charakteryzują 95% Polaków?

µ = 100, σ = 15

0.95 - tyle ma wynosić poziom ufności, czyli prawdopodobieństwo, czyli pole pod krzywą

1 - 0.95 = 0.05 - tyle wynosi poziom istotności α

α /2 = 0.025 - dwustronnie musimy obciąć po 2.5% pola

Ф(-Z) = Ф(0.025) = -1.96

Ф(+Z) = Ф (0.95 + 0.025) = Ф (0.975) = 1.96

P(100 - 1.96 ∙ 15≤ X ≤ 100 + 1.96 ∙ 15) = 0.95

↓ ↓

• 129

95% Polaków charakteryzują ilorazy inteligencji między 70 i 129.

Ф(Z) = 0.95 Z = 1.645 odcinamy jednostronnie

11. Teoria estymacji - teoria szacowania parametrów

estymacja punktowa np. µ ≈

Estymacja punktowa polega na uznaniu, że nieznana wartość parametru jest bardzo zbliżona do estymatora dużej próby wylosowanej z populacji.

P(
- Zα ∙ σ/
≤ µ ≤
+ Zα ∙ σ/
) = 1 - α estymacja przedziałowa

Estymacja przedziałowa polega na zbudowaniu przedziału ufności dla rozkładu estymatora.

• Wyznacz przedział ufności.

P(
- Zα ∙ σ/
≤ µ ≤
+ Zα ∙ σ/
) = 1 - α

x = 110

n = 400

s = 5 σ ≈ s = 5 estymacja punktowa

α = 0.05

Zα dwustr. = 1.96

P(110 - 1.96 ∙ 5/
≤ µ ≤ 110 + 1.96 ∙ 5/
) = 0.95

P(109.51 ≤ µ ≤ 110.49) = 0.95

µ Є <109.51, 110.49>

12.

13. Rozkład prawdopodobieństwa t - studenta

Jeżeli pobieramy kolejno próbki losowe o ustalonej i małej liczebności n z populacji, w której zmienna losowa ma rozkład normalny ze średnią µ i wariancją równą σ², to wraz ze wzrostem liczby losowań rozkład średniej z próby dąży do spłaszczonego rozkładu normalnego. Spłaszczenie jest tym większe, im mniejsza liczebność próby.

Takie rozkłady po wystandaryzowaniu noszą nazwę

rozkładów prawdopodobieństwa t - studenta zmiennej t.

Próbki statystyczne nie mogą mieć mniej niż 3 elementy.

n	s² = (n - 1):(n - 3)	- µ - µ t = --------- ⋅ = -------- s
5	2
6	1.66
7	1.5
100	1.02
130	≈ 1

• Jak będzie wyglądał rozkład, w którym zmniejszono liczebność z 400 do 50 przy

x = 110 i s = 5? Jaki będzie po wystandaryzowaniu?

Będzie to rozkład normalny spłaszczony, który po wystandaryzowaniu będzie rozkładem t - studenta.

P(
- tα,df ∙s/
≤ µ ≤
+ tα,df ∙s/
) = 1- α

P(110 - 2.0102 ∙ 5/
≤ µ ≤ 110 +2.0102 ∙ 5/
) = 1- α

40 - 2.021 50 - 2.009 różnica 10 stopni swobody 2.021 - 2.009 = 0.012

2.012 : 10 = 0.0012 2.009 + 0.0012 = 2.0102

Liczba stopni swobody determinuje kształt rozkładu.

15.

16. Test t - studenta dla dwu populacji niezależnych

Jeżeli pobieramy niezależnie duże próby losowe parami odpowiednio o liczebności n1 i n2 z dwu populacji niezależnych o normalnych rozkładach zmiennej x N(µ1, σ1²) i N(µ2, σ2²), to rozkład z próby różnicy między średnimi (x1 - x2)dąży do rozkładu normalnego ze średnią (µ1 - µ2) oraz wariancją (σ1²/n1 + σ2²/n2).

przykład:

• zmienna X - skala przynajmniej przedziałowa

• 
  
  zmienna X ma normalny rozkład w pierwszej N(µ1, σ1²) i w drugiej N(µ2, σ2²) populacji

• dwie próby losowe o liczebności n1 i n2 µ

• 
  
  α określone subiektywnie przez badacza

• 
  Ho: µ1 = µ2 = µ

• H1: µ1 > µ2

Postać statystyki testu:

(x1 - x2) - (µ1 - µ2) (x1 - x2) - 0

t = ----------------------- = -------------------

σ (x1 - x2) (σ1²/n1 + σ2²/n2)

Zakładamy, że wariancje są homogeniczne σ1² = σ2² = σ²	Zakładamy, że wariancje są heterogeniczne σ1² ≠ σ2²
Należy stworzyć estymator łączny: s1² + s2² (n1 - 1) ⋅s1² + (n2 - 1) ⋅s2² σ² ≈ s = ---------- = ------------------------------ 2 n1 + n2 - 2 n1 ∙ n2 (x1 - x2) ∙ ---------- n1 + n2 t = --------------------------------------- (n1 - 1) ⋅ s1² + (n2 - 1) ⋅ s2² ----------------------------------- n1 + n2 - 2 wykresy pokrywają się f = n1 + n2 - 2	σ1², σ2² szacuje się punktowo Ze względu na heterogeniczność wariancji wprowadza się poprawkę stopni swobody. Należy je zmniejszyć, aby zwiększyć przedział ufności szczuplejszego wykresu. test Coxa - Cochrana t =

17.

18. Test t - studenta dla dwu populacji zależnych

Jeżeli pobieramy kolejno zależne próbki losowe parami o dużej liczebności n z dwu populacji, w których zmienna x1 i x2 mają rozkład normalny, to gdy D = x1 - x2 jest zmienną różnic pomiarów ( w rozkładzie normalnym ze średnią μD i wariancją σ²D, rozkład średniej zmiennej D, xD dąży do rozkładu normalnego ze średnią μD i wariancją σ²D/n.

• populacje zależne

• x1, x2 mierzalne, zależne, D = x1 - x2

• 
  x1 → N(µ1, σ1²)

Jeżeli x1, x2 mają rozkład normalny to xD też

• x2 → N(µ2, σ2²)

• α określone subiektywnie przez badacza

• n - liczebność próby

Ho: μD = 0

H1: μD < 0

-

t = ------------ ⋅
= ---------------------------

² - n ⋅
²

-------------------------------------

(n - 1) ⋅ n

Własnością średnich z populacji zależnych jest to, że średnia z różnic pomiarów jest równa różnicy średnich :
=

19. Zadanie o muzykach

l.p.	S1	S2	di
1	7	10	-3	Dla s2: n = 20
2	6	10	-4	= 13 = 8.42 s = 2.9
3	7	8	-1
4	9	10	-1	Osobno dla s2 : n1 = 10, n2 = 10
5	11	12	-1	fortepianiści: = 11 = 4.22 s = 2.05
6	10	11	-1	skrzypkowie: = 15 = 4.67 s = 2.16
7	10	12	-2
8	9	13	-4	Dla di: n = 20
9	9	9	-0	= -3 = 39.6 s = 6.3
10	12	5	-3
11	8	13	-5	I. Czy można uznać, że przeciętny poziom tremy odczuwany na godzinę przed koncertem
12	10	15	-5	wynosi 15 punktów?
13	10	14	-4	II. Czy prawdą jest, że fortepianiści odczuwają na godzinę przed koncertem wyższy poziom
14	10	15	-5	tremy niż skrzypkowie?
15	20	20	-0
16	12	16	-4	Ad. I
17	9	15	-6	Pytanie dotyczy populacji. Wiemy, że poziom tremy uległ zmianie.
18	11	16	-5
19	9	12	-5
20	11	14	-1	próba populacja

Po wystandaryzowaniu, przy założeniu, że rozkład jest normalny, otrzymamy rozkład

t - studenta.

x ε <13.642, 16.358>

Stan populacji mógł się nie zmienić, a my mogliśmy wylosować próbę z odciętego ogona - obszaru o bardzo małym prawdopodobieństwie.

Dowodzenie nie wprost: Jeżeli twierdzenie, że μ = 15 jest prawdziwe, to średnia może leżeć wyłącznie na odcinku < 13.642, 16.358 >. Średnia w naszej próbie nie należy do tego odcinka, więc odrzucamy hipotezę zerową i przyjmujemy hipotezę alternatywną.

t =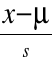
⋅
=
⋅
= -3.084

|-3.084| > tα,df → Ho‾

Ho: μ = 15 Hipotezę zerową przy hipotezie alternatywnej kierunkowej sprawdza się testem

H1: μ < 15 statystycznym jednostronnym.

df = 19 tα,df = 1.729

α = 0.05

|-3.084| > 1.729 → Ho‾

Jeżeli odrzucimy hipotezę zerową testem dwustronnym, to na pewno odrzucimy ją także testem jednostronnym (nie zawsze jest odwrotnie!!!). Testy jednostronne w porównaniu z testami dwustronnymi minimalizują popełnienie błędu II rodzaju - są mocniejsze.

Moc testu - zdolność testu do odrzucenia fałszywych hipotez zerowych równa 1 - β.

Łatwiej odrzucić hipotezę zerową testem jednostronnym.

Ad. II

S2: 1h przed występem

fortepianiści:
= 11
= 4.22 s = 2.05 Skrzypkowie denerwują się bardziej

skrzypkowie:
= 15
= 4.67 s = 2.16 niż fortepianiści.

Jeżeli czynnik (rodzaj instrumentu) nie działa, to μs = μF = μ, czyli μs - μ = 0.

Ho: μs = μF = μ

αi = μs - μ ≠ 0 efekt główny

t =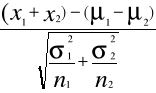

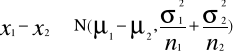
t =
wariancje homogeniczne

t =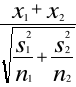
wariancje heterogeniczne (test Coxa - Cochrana)

Ho: σ 1² = σ 2²

H1: σ 1² > σ2²

F =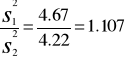

|1.107| < 3.18 →

A 20. Analiza wariancji prosta - ANOVA

- zmienna niezależna ( = kontrolowana, egzogeniczna, objaśniająca)

X - zmienna zależna ( = analizowana, endogeniczna, objaśniana)

1 zmienna analizowana - jednowymiarowa analiza

1 czynnik - jednoczynnikowa wariancji

jednowymiarowa analiza ANOVA

dwuczynnikowa wariancji

jednowymiarowa analiza

k - czynnikowa wariancji

μ1 = μ

μ2 = μ αi = 0

: μ1 = μ2 = μ3 = ... = μk = μ układ równań ... ≡ i = 1,2,3...,k

: ~
...

μk = μ

ANOVA nie uwzględnia porządku kategorii wartości.

- czynnik nie wpływa na X, czyli nie działa, a to znaczy, że nie różnicuje średnich

~
- czynnik działa, czyli jakieś równanie jest zaburzone, a to znaczy, że któraś średnia jest różna od μ

1

próba

populacja

s²x+c = s²x s²c⋅x = c² ⋅ s²x

Stevens

xi ⋅ fi

n

v = 6 ⋅ s

rozkład normalny

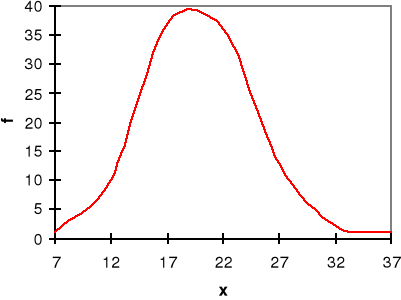
Krzywa Gaussa!!!

Nie zapominajmy o wkładzie pana Moivre'a.

σx = σ/
błąd standard. średniej σx Є < 0, σ >

t - student to W.S. Gosett

σs = σ/
błąd standard. odchylenia standard.

wystandaryzowana średnia z małej próby

n1, x1, s1

n2, x2, s2

µ1, σ1²

µ2, σ2²

weryfikuje hipotezę o równości wariancji

x

x

Badamy tę samą grupę osób w różnych sytuacjach.

D - zmienna różnic

wymiar

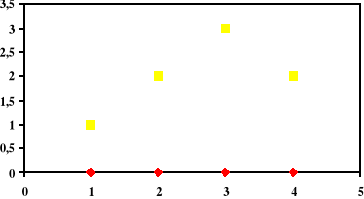
S1: 5h, S2:1h przed koncertem

μ = ?

X→ N(µ, σ²)

= 13 s = 2.9

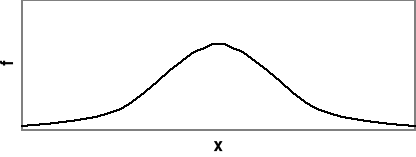
→ N (15,
)

α = 0.05

Ho: μ = 15

H1: μ ≠ 15

Hipotezę zerową przy hipotezie alternatywnej różnościowej sprawdza się testem statystycznym dwustronnym.

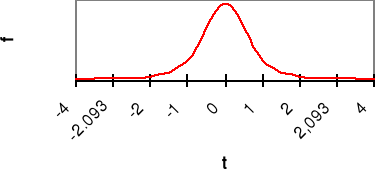
15 - 2.093⋅
= 13.642

15 + 2.093⋅
= 16.358

2.093 to wartość tα,df przy H1 różnościowej

xF → N(µF, σF²)

xs → N(µS, σS²)

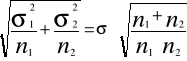
tę wartość sprawdzamy w tablicach

---