Przykład 2 (źródło: Borkowski, [2003], s. 103)

Dane są wartości średniego spożycia owoców, dochody i płeć 12 losowo wybranych osób

Nr	Spożycie owocó (kg)	Dochody (tys. Zł)	Płeć
1	3,8	2,0	Mężczyzna
2	4,7	2,1	Kobieta
3	4,4	1,8	Kobieta
4	5,0	2,7	Kobieta
5	4,1	3,0	Mężczyzna
6	3,7	3,5	Mężczyzna
7	4,9	5,0	Kobieta
8	5,4	4,5	Mężczyzna
9	5,2	4,2	Kobieta
10	4,6	3,8	Mężczyzna
11	4,0	2,4	Mężczyzna
12	3,6	1,4	Mężczyzna

Oznaczmy:

Y - miesięczne spożycie owoców w kg;

X - miesięczne dochody w tys. zł

Z - zmienna zero jedynkowa przyjmująca wartość jeden jeśli badana osoba jest kobietą i zero w pozostałych przypadkach.

Model, który należy oszacować ma postać: Y=α₀+α₁X+α₂Z+ξ

W Excelu wpisujemy dane i uzupełniamy tabelę regresji, tak jak to pokazano na poniższym `rysunku.

Rys 1.: Wpisywanie danych do okna dialogowego Regresji

Po naciśnięciu OK. w okienku regresji pojawi się następująca ramka z wynikami:

Rys. 2: Wyniki działania opcji Regresja - oszacowania modelu ekonometrycznego

W kolumnie zatytułowanej Współczynniki (komórka B16 na rys. 2) znajdują się oszacowane parametry strukturalne, pozwalające nam zapisać model następująco:

Y=3,27+0,31X+0,60Z

Wynika z tego, że oszacowane parametry strukturalne są następujące: α₀=+3,27, α₁=+0,31, α₂=+0,60.

Interpretacja parametrów

Przy założeniu, że model jest poprawny (co sprawdzimy za pomocą szeregu statystyk omawianych poniżej), a parametry istotne statystycznie możemy je zinterpretować jako:

α₁=0,31 oznacza, że wzrost miesięcznych dochodów o 1 tys. zł powoduje wzrost miesięcznego spożycia owoców o 0,31 kg.

α₂=0,60 oznacza, że kobiety spożywają średnio o 0,60 kg owoców więcej od mężczyzn

Wyrazu wolnego α₀=3,27 najczęściej nie interpretuje się.

Błąd średni modelu S_e

Błąd średni nazywany jest również błędem standardowym (np. w Excelu) lub bardziej fachowo odchyleniem standardowym reszt, lub pierwiastkiem z wariancji resztowej. Błąd ten jest liczony na podstawie wartości odchyleń (reszt e_t) pomiędzy wartościami teoretycznymi badanego zjawiska (czyli zmiennej objaśnianej
, wyliczonej z równania ekonometrycznego), a wartościami empirycznymi, czyli oryginalnymi „igrekami”- y_t , które podstawialiśmy do równania przed jego oszacowaniem. Z formalnego punktu widzenia reszty e_t równania są realizacją składnika losowego ξ i pełnią następującą rolę: uzupełniają prawą stronę równania o taką wartość, jaka jest potrzebna, aby można było postawić znak równości pomiędzy prawą i lewą stroną. Pokażemy to na dotychczasowym przykładzie. Przypomnijmy, że oszacowane równania spożycia owoców ma postać:

Y=3,27+0,31X+0,60Z (Y - spożycie owoców w kg. , X - dochody w tys. zł, Z - płeć konsumenta). Na podstawie oszacowanej funkcji możemy wyliczyć teoretyczne, wynikające z oszacowanego równania spożycie owoców. Sposób tego przeprowadzenia ukazuje rys.3.

Rys. 3. Wyliczenie teoretycznych wartości zmiennej objaśnianej (spożycie owoców)

Różnice pomiędzy wartościami empirycznymi y_t (w kolumnie B) i wartościami teoretycznymi
(kolumna E) stanowią reszty równania e_t (wyliczone w kolumnie F). Możemy zapisać zatem, że reszty to:

e_t= y_t -

Ich wartości znajdują się na rys.4.

Rys. 4. Wartości teoretyczne zmiennej objaśnianej (spożycie owoców)

Graficzne odzwierciedlenie reszt przedstawia rys. 5.

Rys. 5. Wykres wartości teoretycznych (linia niebieska) i empirycznych (linia czerwona) w równaniu spożycia owoców

Z powyższego rysunku możemy odczytać, że reszty w poszczególnych przypadkach wynoszą:

e₁=3.8-3.89=-0.09, e₂=4.7-4.52=+0.18, e₃=4.4-4.43=-0.03, e₄=5-4.71=+0.29,

e₅=4.1-4.20=-0.1, e₆=3.7-4.36=-0.66, e₇=4.9-5.42=-0.52, e₈=5.4-4.57=+0.83,

e₉=5.2-5.17=+0.03, e₁₀=4.6-4.45=+0.15, e₁₁=4-4.01=-0.01, e₁₁=3.6-3.70=-0.1.

Z powyższych wyliczeń wynika, że w niektórych okresach mamy do czynienia z dużą trafnością modelu, tzn. różnice pomiędzy wartościami empirycznymi i teoretycznymi prawie nie istnieją (błędy są niewielkie), jak w przypadku e₃, e₉, e₁₁. Istnieją też obserwacje dla których mamy do czynienia z dużą pomyłką modelu, jak np. dla e₆, e₇, e₈. To, ile średnio mylimy się, mówi nam właśnie S_e, czyli średni (standardowy) błąd (odchylenie) modelu.

Liczymy go za pomocą następującej formuły:

gdzie n jest liczbą obserwacji, a k liczbą szacowanych parametrów.

W naszym modelu (spożycia owoców) n=12, k=3, a błąd średni równania wynosi S_e=0.396 (w Excelu jest to komórka B7 zatytułowana Błąd standardowy - por. rys. 2). Wartość ta oznacza, że w modelu spożycia owoców wartości empiryczne odchylają się od teoretycznych o średnio 0.396 kg.. Mówiąc prościej S_e=0.396 oznacza, że szacując model spożycia owoców mylimy się średnio o 0.396 kg.

Z powyższej interpretacji wynikają pewne własności S_e:

1. Błąd S_e jest wyrażony w jednostkach zmiennej objaśnianej. Fakt ten powoduje jego niewielką porównywalność w stosunku do innych modeli (nie ma możliwości przełożenia błędu rzędu 0.396 kg na błąd rzędu np. 0.396 tys. szt.)

2. Błąd S_e nie mówi o skali zjawiska. Np. w naszym przypadku fakt, że w modelu spożycia owoców mylimy się średnio o 0.396 kg nie pozwala nam stwierdzić, czy to dużo, czy mało. To zależy od skali badanego zjawiska. Jeśli jest nim miesięczne spożycie owoców w wieloosobowej rodzinie, gdzie przeciętnie zjada się ok. 10 kg owoców, to taki błąd byłby niewielki. Jeśli natomiast odniesiemy go do spożycia pojedynczych osób, to taka sama miara może oznaczać zupełnie inną skalę błędu. Aby się o tym przekonać, należy odnieść uzyskaną miarę błędu S_e do średniej arytmetycznej badanego zjawiska. W naszym przykładzie średnie spożycie owoców wynosi
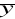
   =(3.8+4.7+4.4+5+4.1+3.7+4.9+5.4+5.2+4.6+4+3.6)/12=53.4/12=4.45 kg. Błąd S_e=0.396 kg stanowi zatem ok. 9% wartości średniej (0.396/4.45≈0.09=9%). Dopiero teraz możemy stwierdzić, czy błąd jest duży, czy mały. W szczególności tak obliczoną miarę możemy porównywać do błędu w innym modelu.

3. Błąd S_e jest miarą nienormowaną, zatem nie można twierdzić, że im niższa wartość błędu, tym lepszy model. Dopiero porównanie błędu ze skalą badanego zjawiska (patrz p. 2) pozwala na tego rodzaju stwierdzenia.

Współczynnik determinacji R²

Współczynnik determinacji mówi nam o stopniu dopasowania modelu do danych empirycznych (a dokładnie jaką część całkowitej zmienności zmiennej objaśnianej stanowi zmienność wyjaśniona przez model). Jest miarą „dobroci” modelu (tzn. wskazuje na ile model jest dobry, a nie zły, jak w przypadku S_e).

Współczynnik determinacji R² określony jest wzorem: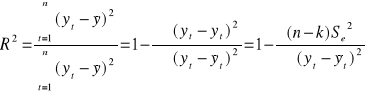

W Excelu znajdujemy go w komórce zatytułowanej R kwadrat. W przypadku zadania dotyczącego spożycia owoców wynosi on R²=0.66 (komórka B5 na rys. 2). R²=0,66 oznacza, że całkowita zmienność spożycia owoców została w 66% wyjaśniona przez model. W uproszczeniu możemy powiedzieć, że model w 66% opisuje badane zjawisko.

Własności R²:

1. R²∈<0;1>

2. R² jest niemalejącą funkcją liczby regresorów, co oznacza, że po włączeniu dodatkowej zmiennej do modelu R² nigdy nie maleje (najczęściej rośnie).

3. Model jest tym „lepszy” (a dokładnie tym większa jest wyjaśniona modelem zmienność zmiennej objaśnianej) im bliższe 1 jest R².

4. R² jest bardzo wysoki w modelach w których występuje silne skorelowanie zmiennych objaśniających między sobą (efekt katalizy).

Dodatkowo prawidłowe użycie współczynnika R² wymaga:

1. Obecności wyrazu wolnego w równaniu (w przeciwnym wypadku należy użyć niescentrowanego współczynnika R²);

2. Liniowej postaci funkcyjnej;

3. Oszacowania modelu KMNK.

Ze względu na powyższe własności współczynnika determinacji oraz możliwość porównań dopasowania dwóch modeli różniących się liczbą zmiennych objaśniających, stosuje się skorygowany współczynnik R².

Skorygowany współczynnik determinacji R²_sk

Skorygowany współczynnik determinacji w Excelu nosi nazwę Dopasowany R kwadrat, (komórka B7 na rys. 2). Posiada on identyczną interpretację co zwykły R², ale nie posiada wszystkich jego własności. R²_sk nie zachowuje dwóch pierwszych własności zwykłego R² a mianowicie:

1. R²_sk może przyjmować wartości ujemne.

2. Wartość R²_sk rośnie jedynie w przypadku wprowadzenia zmiennej mającej istotny wpływ na badane zjawisko. W przeciwnym wypadku (gdy wprowadzamy zmienną nie wywołującą znaczącego przyrostu wyjaśnienia zmienności zmiennej objaśnianej) współczynnik R²_sk maleje. Może on zatem być kryterium wyboru modelu dla różnej liczby zmiennych objaśniających.

Błędy średnie estymatorów
, czyli oszacowanych parametrów

Nazywane są również odchyleniem standardowym estymatorów (oszacowanych parametrów), lub pierwiastkiem z wariancji estymatorów (patrz komentarz do S_e). Błędy te mówią nam o ile średnio mylimy się szacując dany parametr α_j.

Aby wyliczyć błąd S(α_j) należy znać macierz (x^Tx)^-1, której diagonalne elementy pomnożone przez wariancję resztową S_e² (por. rozdział 5) są wariancjami poszczególnych parametrów. Jeśli zatem macierz wariancji kowariancji estymatorów jako D²(α)= S_e²(x^Tx)^-1 , a jej elementy diagonalne jako d_ij to błąd średni (odchylenie standardowe) estymatora (oszacowanego parametru) zapiszemy jako:

W przypadku modelu spożycia owoców otrzymujemy następujące oszacowania parametrów i ich błędy średnie (por. kolumna B i C na rys. 2):

=3.27,
=0.34

=0.31,
=0.10

=0.60,
=0.23

Interpretacja:

=0.34, oznacza, że szacując parametr α₀ mylimy się średnio o 0.34;

=0.10, oznacza, że szacując parametr α₀ mylimy się średnio o 0.10;

=0.23, oznacza, że szacując parametr α₀ mylimy się średnio o 0.23;

Czy to oznacza, że najmniejszym błędem (a zatem największą precyzją szacowania) charakteryzuje się parametr o najmniejszej wartości błędu, czyli 0.10? Oczywiście nie, bowiem wartość błędu parametru trzeba odnieść do wartości tego parametru i dopiero to porównanie pozwala nam stwierdzać precyzję szacowania parametrów. W naszym przypadku błędy parametrów stanowią odpowiednio 10%, 24% i 39% wartości parametrów α₀, α₁, α₂ (0.34/3.27≈0.1=10%; 0.10/0.31≈0.34=34%; 0.23/0.60≈0.39=39%). A zatem to parametr α₀ jest oszacowany z najmniejszym błędem (najbardziej precyzyjnie).

Statystyki t-Studenta

Statystyki t-Studenta służą do testowania istotności parametrów i zmiennych włączonych do modelu. Poniżej zaprezentowany test jest statystycznym narzędziem podejmowania decyzji co do istotności wpływu uwzględnionych w równaniu czynników na zmienną objaśnianą. Wnioskowanie o istotności zmiennych odbywa się pośrednio: poprzez wnioskowanie o istotności parametrów. W tym celu stawiamy następujący zespół hipotez:

H₀: α_j=0 (nieistotność statystyczna)

H₁: α_j≠0 (istotność statystyczna)

Ten zespół hipotez weryfikujemy za pomocą statystyki t postaci:
, mającej rozkład t-Studenta. Następnie należy wybrać właściwą wartość krytyczną rozkładu t-Studenta: t_kr, którą odczytujemy dla: odpowiedniego poziomu istotności (jest to przeciwieństwo poziomu prawdopodobieństwa wnioskowania - poziomu ufności, najczęściej 0.05, czemu odpowiada 95% prawdopodobieństwo testu);

• odpowiedniej liczby stopni swobody równania, która jest różnicą pomiędzy liczbą obserwacji n a liczbą szacowanych parametrów k.

Decyzja o istotności lub jej braku jest następująca:

• jeżeli t_αj<t_kr , to nie ma podstaw do odrzucenia hipotezy zerowej (parametr i ew. zmienna z nim związana są nieistotne statystycznie);

• jeżeli t_αj>t_kr , to odrzucamy hipotezę zerową na korzyść alternatywnej (parametr i ew. zmienna z nim związana mają istotny wpływ na badane zjawisko)

W Excelu wartość krytyczną odczytujemy wybierając odpowiednią funkcję o nazwie ROZKŁAD.T.ODW, gdzie należy wpisać Prawdopodobieństo oraz Stopnie_swobody- patrz rys. 6.

Rys. 6. Generowanie wartości krytycznej rozkładu t-Studenta

W naszym przykładzie wpisujemy prawdopodobieństwo: 0.05 oraz liczbę stopni swobody: 9 i otrzymujemy wartość krytyczną t_kr=2.26.

Wartości statystyk t-Studenta dla kolejnych parametrów podaje kolumna D na rysunku 2. Są one następujące: t_α0=
=9.66, t_α1=
=2.96, t_α0=
=2.59.

Ponieważ t_α0=9.66>2.26=t_kr zatem parametr α₀ ma istotny wpływ na badane zjawisko (spożycie owoców).

Ponieważ t_α1=2.96>2.26=t_kr zatem parametr α₁ ma istotny wpływ na badane zjawisko (spożycie owoców).

Ponieważ t_α2=2.59>2.26=t_kr zatem parametr α₁ ma istotny wpływ na badane zjawisko (spożycie owoców).

Ponieważ parametry α₁ i α₂ są związane z czynnikami determinującymi spożycie owoców, zatem wniosek o ich istotności rozciąga się na wniosek o istotności zmiennych. Możemy zatem stwierdzić, że zarówno dochody, jak i płeć ma istotny wpływ na spożycie owoców.

Przedziały ufności dla parametrów:

Przedziały ufności wyznaczają granice w których znajdą się wartości parametrów z góry określonym prawdopodobieństwem. Wyznaczanie przedziałów ufności nazywane jest również estymacją przedziałową bo zamiast konkretnej, jednej wartości estymatora (oszacowanego parametru) wyznacza się prawdopodobny przedział jego wartości, wg wzoru: α_j∈(
), gdzie:

α_j - prawdziwa wartość parametru α_j,

- estymator (oszacowanie) parametru α_j,

t_kr - wartość krytyczna rozkładu t- Studenta dla n-k stopni swobody i z góry ustalonym prawdopodobieństwie,

- błąd średni estymatora (oszacowania) α_j.

Przedziały ufności mówią nam, że przy danym prawdopodobieństwie przedział o podanych krańcach pokryje prawdziwą wartość badanego parametru.

Dla modelu spożycia owoców, otrzymujemy następujące przedziały ufności dla 95% prawdopodobieństwa (kolumny F i G na rys. 2):

α₀∈(2.50;4.04), α₁∈(0.07;0.54), α₂∈(0.08;1.13).

Oznacza to, że:

• przedział o krańcach (2.50;4.04) z 95% prawdopodobieństwem pokryje prawdziwą wartość parametru α₀

• przedział o krańcach (0.07;0.54) z 95% prawdopodobieństwem pokryje prawdziwą wartość parametru α₀

• przedział o krańcach (0.08;1.13) z 95% prawdopodobieństwem pokryje prawdziwą wartość parametru α₀.

UWAGA

W Excelu można dowolnie ustalić prawdopodobieństwo przedziału ufności, co spowoduje wyświetlenie się w dwóch ostatnich kolumnach przedziałów dla nowego prawdopodobieństwa. Aby to uczynić należy zaznaczyć pole Poziom ufności (por. rys. 1) i ustawić żądany poziom. Poniżej znajdują się wyniki dla modelu spożycia owoców wraz z 99% przedziałami ufności.

Rys. 7. Wyniki regresji równania spożycia owoców z dodatkowym, 99% przedziałem ufności dla parametrów

Jak widzimy zwiększenie prawdopodobieńśtwa (lub inaczej mówiąc zmniejszenie poziomu istotności) powoduje rozszerzenie przedziału ufności.

Różnice w znakach reszt wynikające z wyliczania ich jako e_t= y_t -
lub jako e_t=
y_t - nie mają znaczenia dla dalszych obliczeń w których bierze się pod uwagę albo kwadraty, albo moduły reszt.

Wbrew temu, co podaje Excel należy tutaj wpisać poziom istotności, a nie prawdopodobieństwo, czyli chcąc wnioskować z 90% prawdopodobieństwem, należy wpisać 0.1.

1

---