Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej |
||||||||
Nazwisko i imię Tomasz Huk studenta: |
Symbol grupy MD 103.1c |
|||||||
Data wykonania ćwiczenia: 18.11.99
|
Symbol ćwiczenia: 1.1 |
Temat zadania: Wyznaczanie współczynnika załamania światła z pomiarów kąta załamania oraz kąta granicznego |
||||||
Zaliczenie: |
Ocena: |
Data: |
Podpis |
|||||
1.Tabela pomiarów.
nr próbki |
Lp. |
alfa |
beta |
n |
gamma |
n z gamma |
n sr |
|
|
|
|
|
|
|
|
|
1 |
20 |
14 |
1,4138 |
|
|
|
|
2 |
25 |
17 |
1,4455 |
|
|
|
|
3 |
30 |
20,5 |
1,4277 |
|
|
|
|
4 |
35 |
24 |
1,4102 |
|
|
|
I |
5 |
40 |
27 |
1,4159 |
43,5 |
1,4533 |
1,4310 |
|
6 |
45 |
29,5 |
1,4360 |
|
|
|
|
7 |
50 |
32 |
1,4456 |
|
|
|
|
8 |
60 |
37 |
1,4390 |
|
|
|
|
9 |
70 |
41 |
1,4323 |
|
|
|
|
10 |
80 |
43 |
1,4440 |
|
|
|
|
1 |
20 |
14 |
1,4138 |
|
|
|
|
2 |
25 |
17 |
1,4455 |
|
|
|
|
3 |
30 |
20 |
1,4619 |
|
|
|
III |
4 |
35 |
23 |
1,4680 |
43,5 |
1,4533 |
1,4590 |
|
5 |
40 |
26 |
1,4663 |
|
|
|
|
6 |
45 |
29 |
1,4585 |
|
|
|
|
7 |
50 |
31,5 |
1,4661 |
|
|
|
|
8 |
55 |
34 |
1,4649 |
|
|
|
|
9 |
60 |
36 |
1,4734 |
|
|
|
|
10 |
65 |
38 |
1,4721 |
|
|
|
2. Obliczenia.
![]()
=![]()
1,4138
![]()
=1,4533
![]()
=1,4310
3. Krótka teoria.
Światło jest falą elektromagnetyczną o długości.l rzędu 4·10 m - 7,6·10 m (4000 A - 7600 A), przy czym za promień świetlny uznano kierunek, wzdłuż,którego przenosi się energia tej fali. W ośrodku jednorodnym, promieniem fali będzie normalna do powierzchni fazowej.
Rys. 1.2 ilustruje zjawisko odbicia i załamania promienia świetlnego na granicy ośrodków I i II. SO jest promieniem padającym,
S01 - promieniem odbitym zaś OP - promieniem zalamanym. Punkt 0 nazywamy punktem padania. Prostą NNl, proatopadłą do powierzchni rozgraniczającej wystawioną
w punkcie 0, nazywamy normalną padania.
SON =alfa,nazywa się kątem padania,kąt NOS1 =alfa prim- kątem odbicia a kąt NOP = beta - kątem załamania.
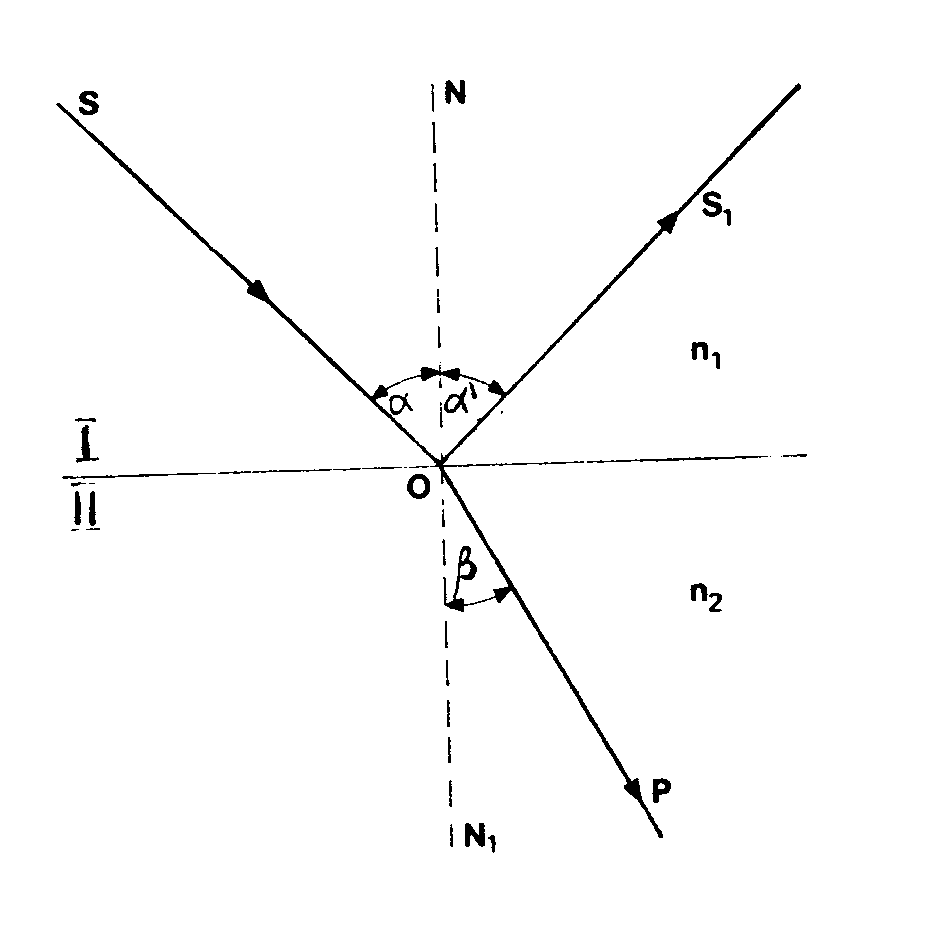
rys. 1.2. Odbicie i załamanie promienia świetlnego na granicy dwu ośrodków.
Prawo odbicia i załamania brzmi następująco:
1. promień padający, odbity i załamany oraz normalna padania leżą w jednej płaszczyźnie,
2, kąt odbicia jest równy kątowi padania,
3. stosunek sinusów kąta padania i kąta załamania promienia swietlnego jest wielkością stałą dla danych dwu ośrodków
i określonej długości fali ; nazywamy go współczynnikiem za· łamania ośrodka II względem I
Jeżeli promień świetlny biegnie z ośrodka optycznie gę
stszego do ośrodka optycznie rzadszego, to na granicy tych ośrodkdw ulega on załamaniu, odchylając się od normalnej padania. W miarę wzrosta kąta padania alfa promień załamany coraz bsrdziej odchyla się od normalnej i przy pewnym kącie alfa = gamma promień załamany biegnie wzdłuż powierzchni granicznej, czyli beta=90 stopni.
Przy kącie alfa>gamma, promień padający nie przejdzie do ośrodka I,
lecz ulegnie calkowitemu odbiciu na granicy ośrodków. Kąt gamma nazywamy kątem granicznym i możemy go wyrazić w następujący sposób:
4.Schemat ćwiczenia i opis wykonania.
W celu wyznaczenia współczynnika załamania, napełniamy badaną cieczą płaską kuwetę w kształcie półwalca. Następnie kuwetę (ewentualnie cialo stałe o ksztalcie półwalca ustawiamy centralnie na tarczy z podziałką kątową, tak aby płaska ściana boczna kuwety pokrywala się ze średnicą tarczy, Po ustawieniu kuwety rzucamy na jej płaską ścianę, w punkcie centralrlym tarczy wąski strumień światła z lampki mikroskopowej
i mierzymy kąt padania oraz kąt załamania, Pomiary przeprowadzamy dla dziesięciu różnych kątów alfa. Następnie oświetlając kuwetę od strony wypukłej, znajdujemy kąt graniczny.
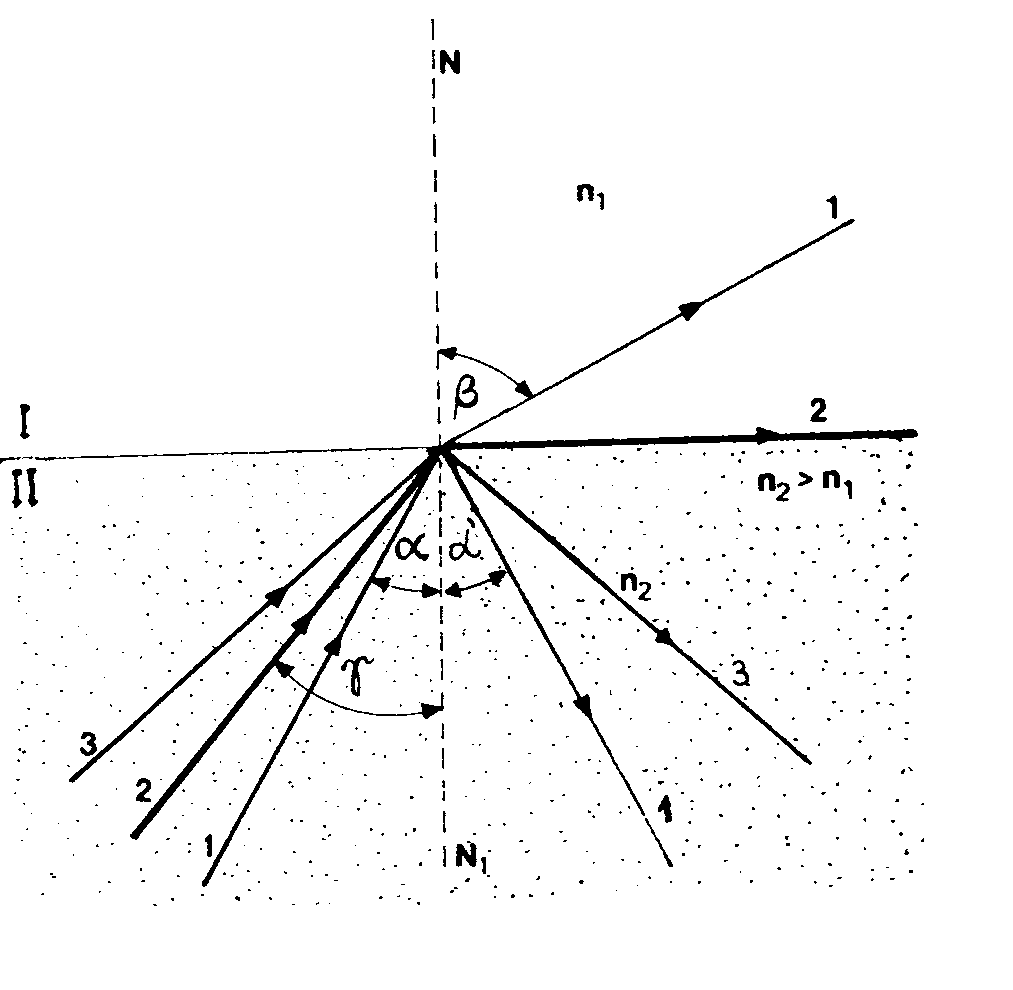
Rys. 1 .3. Przejście promienia świetlnego z ośrodka optycznie gęstrzego do rzadszego.
5. Opracowanie wyników pomiarów.
Błąd względny maksymalny-metoda różniczkowa.
![]()
![]()
![]()
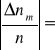
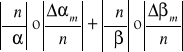
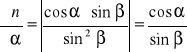
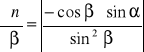
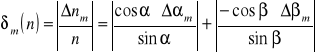
Dla próbki numer 1.
![]()
![]()
![]()
![]()
+ ![]()
=![]()
0,017 + ![]()
0,017 =0,00619 +0,01956 = 0,02574
i wyrażając w procentach :
![]()
0,02574 100% = 2,574%
błąd bezwzględny maksymalny wynosi :
![]()
n =![]()
n = 0,02574 1,4323 = 0,0369
wynik pomiaru zapiszemy :
n = (n ![]()
![]()
)
n = (1,4323 ![]()
0,0369)
1,3954 < n < 1,4692
Dla próbki numer 3.
![]()
![]()
![]()
![]()
+ ![]()
=![]()
0,017 + ![]()
0,017 =0,017 + 0,0306 = 0,0476
i wyrażając w procentach :
![]()
0,0476 100% = 4,76%
błąd bezwzględny maksymalny wynosi :
![]()
n =![]()
n = 0,0476 1,4585 = 0,0694
wynik pomiaru zapiszemy :
n = (n ![]()
![]()
)
n = (1,4585 ![]()
0,0694)
1,3891 < n < 1,5279
Ponieważ dla obu próbek wartość kąta ![]()
jest taka sama to błąd względny maksymalny względem ![]()
liczymy tylko jeden raz.
n = ![]()
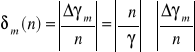
![]()
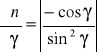
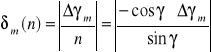
![]()
0,017 rad
![]()
![]()
=0,017915
i wyrażając w procentach :
![]()
0,0179 100% = 1,79%
błąd bezwzględny maksymalny wynosi :
![]()
n =![]()
n = 0,017915 1,4585 = 0,02613
wynik pomiaru zapiszemy :
n = (n ![]()
![]()
)
n = (1,4585 ![]()
0,02613)
1,4324 < n < 1,4846
1
4
Wyszukiwarka
Podobne podstrony:
INZ LAB 4 CW, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, Sprawozdania-dokumenty,
Elektrotechnika - ćw.3, Politechnika Lubelska, Studia, Studia, Elektrotechnika - laboratorium, Elekt
SprawozdaniePrzekroje ćw.3, Politechnika Lubelska, Studia, Studia, Sprawozdania 2 semestr
M 6 3, Politechnika Lubelska, Studia, Studia, fizyka
J 5 1, Politechnika Lubelska, Studia, Studia, fizyka
O 9 1, Politechnika Lubelska, Studia, Studia, fizyka
ENERGOELEKTRONIKA 3 - PROTOKÓŁ, Politechnika Lubelska, Studia, semestr 5, Semest V, od grzechu, mój
M-14.1P, Politechnika Lubelska, Studia, Studia, fizyka
Ćwiczenie 00, Politechnika Lubelska, Studia, Studia, fizyka
E3.2, Politechnika Lubelska, Studia, Studia, fizyka
Ściąga-Fizyka ED 7, Politechnika Lubelska, Studia, Studia, sem VI, z ksero na wydziale elektrycznym
Test-Fizyka ED 7, Politechnika Lubelska, Studia, Studia, sem VI, z ksero na wydziale elektrycznym
WSTĘP 44, studia mechatronika politechnika lubelska, Studia WAT, semestr 2, FIZYKA 2, LABORKI, labor
M 10 2, Politechnika Lubelska, Studia, Studia, fizyka
mech5.2, Politechnika Lubelska, Studia, Studia, fizyka
więcej podobnych podstron